
|
Met een analoog naar digitaal omzetter (ADC) zet u een analoog signaal om in een digitale code waarvan het 'gewicht' recht evenredig is met de momentane waarde van de analoge spanning.
|
Het algemene principe van ADC
Inleiding
Digitaliseren of kwantiseren noemt men het omzetten van een analoge spanning in een digitale code. U kunt denken dat digitaliseren een probleemloos proces is. U voert de analoge spanning toe aan de ingang van de ADC, op de uitgangen ontstaan de digitale codes die de momentane grootte van de analoge spanning representeren. Niets is echter minder waar! Bij het kwantiseren van analoge signalen moet u met enkele wetmatigheden rekening houden, die in de volgende paragraafjes besproken worden.
Het bemonsteren of samplen
Op de eerste plaats is het een gegeven dat de meeste ADC's niet continu werken. Als namelijk de digitale code op de uitgang zich continu zou aanpassen aan de amplitude veranderingen van het analoog ingangssignaal, dan zou er een echte code-chaos ontstaan op de uitgang van de omzetter. Het omzetten van de analoge spanning in een digitale code is een proces dat namelijk niet traagheidsloos verloopt. Deze conversie-tijd ligt zelfs bij de snelste omzetters in het ns bereik. Een moderne snelle ADC heeft een sampling rate van 50 MSa/s (lees verder). Dat wil zeggen dat zo'n schakeling 50.000.000 samples per seconde neemt van het ingangssignaal. Het ene uitgangsbit zal iets sneller reageren dan het andere. Als u continu omzet, dan zou de digitale code per ongeluk worden uitlezen op het moment dat een of meerdere bits bezig zijn zich aan de nieuwe analoge ingangssituatie aan te passen. De digitale code kan op dat moment volledig foute informatie bevatten.
Sample and hold
Om dat probleem te voorkomen moet u het analoog signaal op vaste tijdstippen bemonsteren. Dat wil zeggen dat u met regelmatige tijdsintervallen een monstertje neemt van de momentane waarde van het ingangssignaal, dit monstertje even opslaat in een analoog geheugen en nadien dit monster omzet in de bijbehorende digitale code. Nadat de omzettingstijd van de ADC is verstreken en u zeker weet dat de digitale code zich aan de nieuwe waarde van het monster heeft aangepast, kunt u de digitale code uitlezen en verder verwerken.
Nadien kunt u een nieuw monster nemen en kunt u het proces herhalen.
Het analoog geheugen waarin het monster van het analoog ingangssignaal even wordt bewaard, wordt steeds uitgevoerd onder de vorm van een 'sample and hold', afgekort tot S&H. Het komt er op neer dat de momentane grootte van het ingangssignaal even wordt opgeslagen in een heel klein condensatortje dat in de meeste gevallen in de ADC-chip is geïntegreerd.
In de onderstaande figuur het is het blokschema van zo'n sample and hold voorgesteld.
 |
Het principe van een sample and hold. (© 2021 Jos Verstraten) |
De sample frequentie en sample rate
Het digitaliseren van een analoge spanning is dus geen continu proces, maar een proces dat gestuurd wordt door een externe klokpuls. De frequentie van dit kloksignaal noemt men de sample frequentie. Deze frequentie bepaalt dus hoeveel samples er per seconde van de analoge ingangsspanning worden genomen. Deze grootheid noemt men de sample rate en wordt uitgedrukt in Sa/s, samples per seconde. Uiteraard heeft men het tegenwoordig over MSa/s en zelfs GSa/s, dus hoeveel miljoen of miljard samples er per seconde worden genomen.
De minimaal noodzakelijke sample frequentie
Een belangrijke vraag is hoeveel monsters u minimaal per seconde moet nemen om het analoog ingangssignaal goed te bemonsteren. Vergeet niet dat het waarschijnlijk de bedoeling is dat die digitale monsters ooit weer worden omgezet in een analoog signaal. Wij, onvolmaakte mensen, hebben immers als gevolg van de traag werkende evolutie nog steeds zintuigen die uitsluitend analoog werken. U moet er dus voor zorgen dat het herwonnen analoog signaal zo goed mogelijk op het origineel signaal lijkt.
Het zal wel duidelijk zijn dat de kwaliteit van het systeem verbetert naarmate u meer monsters neemt. Vandaar dat men alleen geïnteresseerd is in de vraag hoe weinig monsters u moet nemen om er toch nog zeker van te zijn dat de digitale codes later in een DAC omgezet kunnen worden in een analoog signaal dat lijkt op het analoog signaal aan de ingang van de ADC. In de onderstaande figuur is het ADC + DAC procedé nog eens grafisch samengevat.
Van één periode van een sinusvormig signaal worden tien monsters genomen.
 |
| Het ADC + DAC proces grafisch samengevat. (© 2021 Jos Verstraten) |
U kunt dus in dit voorbeeld stellen dat de sampling frequentie tien maal groter is dan de signaalfrequentie. In de onderste grafiek zijn deze tien digitale monsters voorgesteld door hun herwonnen analoge waarden op de uitgang van de DAC. De originele periode van de sinus wordt benaderd door tien opeenvolgende stapspanningen.
In het getekende voorbeeld kunt u uit deze stapvormige benadering zonder al te veel fantasie de vorm van het originele signaal herkennen. U kunt echter niet grenzeloos verder gaan met het reduceren van de sampling frequentie.
Het sampling theorema
Wiskundig kan worden aangetoond dat de sampling frequentie minstens twee maal groter moet zijn dan de hoogste frequentie in het analoog signaal. Deze algemene wet staat bekend als het 'sampling theorema'. Sampelt u met een lagere frequentie, dan is het absoluut onmogelijk om de vorm van het originele analoog signaal uit de opeenvolgende digitale samples terug te winnen.
U kunt dit effect heel mooie grafisch aantonen. In de onderstaande figuur wordt een sinusvormige analoge spanning met een frequentie van 15 kHz gesampeld met een frequenties die steeds lager worden. Als u nadien de opeenvolgende digitale codes met een DAC omzet in de herwonnen analoge spanning ontstaat een signaal dat een stapvormige benadering van het sinussignaal zou moeten zijn. Dat klopt nog vrij aardig als u sampelt met een frequentie van 7,5 kHz. Maar naarmate de sample frequentie steeds lager wordt zal het herwonnen analoog signaal steeds minder op de originele sinus gaan lijken. Bij zeer lage frequenties is het herwonnen signaal zelfs niet eens meer als sinus herkenbaar, maar wordt het een driehoek!
Deze veel lagere frequentie noemt men de 'alias frequentie' en de grote vervorming die in dit geval ontstaat de 'alias vervorming'.
 |
| Een voorbeeld van het 'sampling theorema'. (© 2021 Jos Verstraten) |
Anti-alias filter absoluut noodzakelijk
Kans op alias vervorming is steeds aanwezig als u bemonstert met een frequentie die lager is dan twee keer de hoogste frequentie in het analoog signaal. Als u een ingangssignaal moet samplen met een bekende vaste frequentie kunt u deze alias vervorming vermijden door de sample frequentie minstens twee maal hoger te kiezen.
Heeft het ingangssignaal een onbekende bandbreedte, dan moet u er kunstmatig voor zorgen dat de frequentieband van het analoog ingangssignaal nooit groter kan zijn dan een bekende waarde. U kunt dan de sample frequentie instellen op twee maal deze bekende waarde.
Het beperken van de bandbreedte van een analoog signaal kan door gebruik te maken van een zeer scherp afsnijdend laagdoorlaat filter. Dit filter wordt gedefinieerd door een bepaalde afsnij-frequentie f0. Het filter laat alle signalen met een frequentie kleiner dan deze afsnij-frequentie door en spert alle signalen die een frequentie hebben die hoger is dan de afsnij-frequentie. Dit laagdoorlaat filter wordt in de ADC/DAC-terminologie het 'anti-alias filter' genoemd. Een logische naam, want dank zij dit filter hebt u geen last meer van alias vervorming. Het volstaat de sample-frequentie gelijk te maken aan 2 x f0 van het filter.

Blokschema van een ADC-systeem
Het blokschema van een bruikbare analoog naar digitaal omzetter is getekend in de onderstaande figuur. Het te digitaliseren analoog signaal wordt eerst door het anti-alias filter gevoerd en gaat vervolgens naar de S&H. De uitgang van deze schakeling gaat naar de analoge ingang van de ADC.
 |
| Het blokschema van een analoog naar digitaal omzetting. (© 2021 Jos Verstraten) |
Specificaties en eigenschappen van ADC's
De woordlengte
Met woordlengte wordt het aantal bits gedefinieerd dat u gebruikt om het analoog signaal om te zetten in een digitale code. Werkt u met een systeem met acht bits (een vaak gebruikte standaard) dan spreekt men van een woordlengte van 8 bit.
Het gewicht van de bits en het MSB en LSB
In het onderstaande voorbeeld is een zaagtandvormig stijgende analoge spanning getekend met een maximale waarde van 15 V. Deze wordt gekwantificeerd door middel van een ADC met vier bits. Deze schakeling levert de standaard binaire code. De kloksnelheid is gelijk aan zestien keer de snelheid van de zaagtand. In de tabel ziet u de samenstelling van de vier bits bij iedere klokpuls. Wat hierbij opvalt is dat het bit Qa van waarde verandert bij iedere volt stijging van de zaagtand. Bit Qb verandert van waarde na iedere 2 V stijging van de zaagtand. Het vierde bit Qd verandert slechts één keer van waarde en wel bij een zaagtandspanning van 8 V. Het is dus mogelijk aan ieder bit een bepaald 'gewicht' toe te kennen. Bit Qa is het 'lichtst', bit Qd het 'zwaarst'. Een waardeverandering van Qa komt immers slechts overeen met een analoge spanningsverandering van 1 V. De waardeverandering van Qd kont echter overeen met een analoge waardeverandering van 8 V.
Vandaar dat men het bit Qa het 'Least Significant Bit' noemt, afgekort tot 'LSB' en het bit Qd het 'Most Significant Bit', afgekort tot 'MSB'.
 |
| De begrippen 'LSB' (Qa) en 'MSB' (Qd) toegelicht. (© 2021 Jos Verstraten) |
De resolutie
De resolutie van een ADC geeft aan in hoeveel kwantiseringsgebieden u het analoog signaal na digitalisatie kunt onderbrengen. Het zal duidelijk zijn dat een systeem met een woordlengte van één bit een resolutie heeft van slechts twee. U kunt de resolutie berekenen door het cijfer 2 te verheffen tot de macht van het aantal bits. Een systeem met een woordlengte van 16 bits heeft dus een resolutie van 216 = 65.536. Met een dergelijk systeem kunt u de momentane waarde van de analoge spanning onderbrengen in 65.536 kwantiseringsgebieden.
Het dynamisch bereik
Het dynamisch bereik geeft de logaritmische verhouding weer tussen de minimale en de maximale signaalverandering die een ADC/DAC-systeem in het analoog signaal kan veroorzaken. De maximale signaalverandering ontstaat als alle bits opeens omschakelen van 'L' naar 'H' of vice versa.
De minimale signaalverandering ontstaat als alleen het minst belangrijke bit omschakelt van de ene naar de andere logische stand.
Het zal duidelijk zijn dat het dynamisch bereik toeneemt naarmate u meer bits bij de omzetting betrekt. Hoe groter de woordlengte, hoe groter het dynamisch bereik. Het dynamisch bereik wordt uitgedrukt in dB en wordt ook wel eens de signaal/ruis-verhouding van de ADC genoemd.
De bitgrootte
De bitgrootte geeft aan met hoeveel mV het analoog ingangssignaal moet dalen of stijgen om het minst belangrijke bit van de ADC van logisch niveau te laten veranderen. De bitgrootte en het dynamische bereik zijn dus in feite twee grootheden die hetzelfde fysische verschijnsel beschrijven. Maar terwijl het dynamische bereik een verhouding weergeeft en dus onafhankelijk is van de maximale grootte van de spanning, is het alleen zinvol de bitgrootte op te geven als u weet wat de maximale amplitude is die het systeem moet verwerken.
Verband tussen woordlengte, resolutie, dynamisch bereik en bitgrootte
Tussen de vier besproken grootheden van een ADC bestaat een wiskundige verband. Dit verband is voor een aantal resoluties samengevat in de onderstaande tabel.
 |
Verband tussen woordlengte, resolutie, dynamisch bereik en |
De offsetfout
Als u aan een ADC een spanning van exact 0 V legt, dan zouden alle uitgangen van de chip 'L' moeten zijn. Vaak zijn een paar minst belangrijke bits echter niet 'L', maar vormen een combinatie van 'L' en 'H'. Dit noemt men de offsetfout van de ADC.
De hysteresisfout
De hysteresisfout is een typische afwijking van ADC's. De hysteresisfout geeft aan dat de spanningsdrempel waarop de uitgang van de ene code naar de andere omschakelt niet constant is, maar afhankelijk van de richting waarin de analoge ingangsspanning varieert. Stijgt deze spanning, dan zal de uitgang dus bij een andere drempel omschakelen dan wanneer de ingangsspanning daalt.
De niet-lineariteit
Zoals de naam reeds doet vermoeden definieert de niet-lineariteit van een ADC de mate waarin de uitgangskarakteristiek afwijkt van een rechte lijn. Dit verschijnsel wordt grafisch toegelicht in de onderstaande figuur. Als u aan een ADC een zaagtandvormige spanning aanlegt, moet het IC het gewicht van zijn uitgangscode met één bit verhogen of verlagen bij iedere verandering van de spanning met één bitgrootte ΔU. Dit is grafisch voor te stellen door de linker grafiek in de onderstaande figuur. Het verhogen van het gewicht van de code met één bit is voorgesteld door de trapvormige benadering van de zaagtandspanning. Op de verticale as zijn de opeenvolgende bitgroottes ΔU voorgesteld waarop het gewicht met één trapje stijgt of daalt. Iedere code-overgang is bij deze ideale ADC het gevolg van een identieke ΔU.
In de rechter grafiek is (overdreven) voorgesteld wat een niet-lineair werkende ADC doet. Nu zijn er verschillende waarden van ΔU nodig om één code-overgang te genereren.
 |
| Het verschijnsel niet-lineariteit grafisch toegelicht. (© 2021 Jos Verstraten) |
De niet-monotone fout
Een ADC met een niet-monotone fout zal, zoals getekend in de onderstaande figuur, op één of op verschillende plaatsen in zijn uitgangskarakteristiek een dalende stap hebben in plaats van een stijgende stap. Dit niet-monotoon gedrag is een rechtstreeks gevolg van een systeem met een grote niet-lineariteit. Zolang de niet-lineariteit kleiner is dan ½ LSB werkt de schakeling gegarandeerd monotoon. Is de niet-lineariteit groter dan ½ LSB, dan kàn de schakeling niet-monotoon zijn, maar zeker is dat niet. Een niet-monotone ADC kan bij sommige toepassingen tot grote systeemfouten leiden.
 |
| Het verschijnsel niet-monotonie grafisch toegelicht. (© 2021 Jos Verstraten) |
Soorten analoog naar digitaal omzetters
De zeven meest gebruikte systemen besproken
Er zijn in de loop der jaren diverse systemen ontwikkeld waarmee u een analoge spanning kunt omzetten in een digitale code. Sommige van deze systemen zijn nu verouderd, maar wij gaan deze tóch voor de volledigheid ook in het kort bespreken. De zeven onderstaande typen ADC's zult u in de praktijk het vaakst aantreffen en wij zullen in de volgende hoofdstukken deze uitgebreid bespreken:
- Ramp-and-compare ADC (RAC-ADC)
- Dual-slope ADC
- Counter-type ADC (DRAC-ADC)
- Tracking ADC
- Successive approximation ADC (SAR-ADC)
- One step flash ADC
- Two step flash ADC
De ramp-and-compare ADC (RAC-ADC)
Het werkingsprincipe
In de onderstaande figuur is het blokschema van dit systeem voorgesteld. Hart van de schakeling is een zeer stabiele condensator C1 en een zeer stabiele constante stroombron Icte. Een meetcyclus start op het moment t0. Vóór dit moment zorgt de TIMER EN KLOK ervoor dat de elektronische schakelaar S1 is gesloten. De FLIP-FLOP en de BINAIRE TELLER zijn gereset. De condensator C1 is kortgesloten door de elektronische schakelaar en is volledig ontladen. De stroom Icte vloeit af naar de massa via deze schakelaar. De te digitaliseren analoge spanning gaat naar één ingang van de COMPARATOR, de spanning over de condensator C1 naar de tweede ingang.
Op het moment t0 geeft de TIMER EN KLOK een signaal aan de schakelaar, waardoor deze opent. De stroom Icte gaat nu de condensator C1 lineair opladen. Op hetzelfde moment geeft de TIMER EN KLOK een SET-puls aan de FLIP-FLOP. De uitgang van dit blok activeert via de TEL-puls de BINAIRE TELLER en deze begint de pulsen te tellen van een zeer stabiele pulsgenerator in het blok TIMER EN KLOK.
Deze actie gaat verder tot de spanning over de condensator C1 is gestegen tot de momentane waarde van de ingangsspanning. De comparator klapt om en geeft een RESET-puls aan de FLIP-FLOP. Deze gaat naar zijn rustpositie waardoor de TEL-puls voor de BINAIRE TELLER weg valt.
Het systeem heeft nu één omzettings-cyclus doorlopen en wacht tot de TIMER EN KLOK een volgende startpuls geeft.
Vanwege de lineaire oplading van de condensator heeft de BINAIRE TELLER een aantal pulsen geteld dat recht evenredig is met de grootte van de ingangsspanning. Ga maar na: stel dat bij de volgende cyclus de ingangsspanning tot de helft is gedaald. Het zal duidelijk zijn dat dan ook het tijdsinterval t0 ~ t1 tot de helft is gereduceerd. Ook het aantal getelde pulsen is dan gehalveerd.
 |
| Het blokschema van een ramp-and-compare ADC. (© 2021 Jos Verstraten) |
Het voordeel van de ramp-and-compare ADC
Het enige voordeel is dat het een eenvoudig systeem is dat vrij weinig elektronica kost om te realiseren. Iedere geoefende elektronica hobbyist zou het kunnen ontwerpen. Heel lang geleden, in de begintijd van de digitale elektronica, werden met RAC-ADC's digitale voltmeters ontwikkeld. Ter illustratie van de eenvoud van een dergelijk systeem ziet u in de onderstaande figuur het volledig schema (minus de voeding) van de EVM100, een digitale voltmeter met een bereik tot +999 mV, die in 1973 (!) door de auteur van dit artikel werd ontworpen voor de firma Thomson Elektronik in Duitsland. De constante stroombron die een condensator oplaadt is hier vervangen door een integrator IC2 die de condensator C2 lineair oplaadt uit een constante spanning die wordt gegenereerd door de diode DZ3. IC1 is als comparator geschakeld, die de ingangsspanning vergelijkt met de lineair stijgende spanning op de uitgang van de integrator IC2.
De volledige besturingslogica zit in de IC'tjes IC3, IC4 en IC5. De pulsen van IC5a worden geteld door drie 7490 tientellers en gedecodeerd naar de nixie-buisjes door drie stuks 74141.
 |
| Een oeroud schema van een ramp-and-compare ADC in een digitale voltmeter. (© De Muiderkring) |
De nadelen van de ramp-and-compare ADC
Bij de bespreking van het blokschema werd tot drie keer toe het begrip 'zeer stabiel' gebruikt: een zeer stabiele condensator, een zeer stabiele stroombron en een zeer stabiele pulsgenerator. Dat is het grote nadeel van dit eenvoudig systeem. Er zitten nogal wat zeer kritische blokken in het geheel, die ieder voor zich de nauwkeurigheid van de ADC bepalen. Als een van die blokken een instabiliteit vertoont, bijvoorbeeld door het verhogen van de omgevingstemperatuur, dan gaat de nauwkeurigheid van het systeem de mist in.
Een tweede nadeel is dat een RAC-ADC heel erg traag is en een meetcyclus heel wat tijd in beslag neemt.
De dual-slope ADC
Het werkingsprincipe
De dual-slope ADC is in feite een verfijning van de RAC-ADC, die ook voornamelijk wordt toegepast in digitale universeelmeters. Het principe van analoog naar digitaal omzetting volgens het dual-slope principe is geschetst in onderstaande figuur. Rond een operationele versterker IC1 is een integrator opgebouwd met tijdconstante RC die, door middel van schakelaar S, de te meten ingangsspanning Uin of een zeer nauwkeurige en stabiele referentiespanning Uref integreert. De Uref moet de tegengestelde polariteit hebben van de ingangsspanning. De fundamentele eigenschap van een integrator is dat de uitgangsspanning lineair stijgt of daalt, afhankelijk van de polariteit van de ingangsspanning.
De uitgangsspanning van de integrator wordt in comparator IC2 vergeleken met de nul. Gedurende een bepaalde constante tijd t1 wordt de ingangsspanning Uin geïntegreerd. Als u er van uitgaat dat de integratiecapaciteit C volledig was ontladen, zal de uitgangsspanning van de integrator na tijdsverloop t1 alleen maar worden bepaald door de grootte van de ingangsspanning. Alle andere factoren die de integrator definiëren (R, C en t1) zijn immers constant. Na t1 wordt de elektronische schakelaar S omgeschakeld en zal de referentiespanning de condensator gaan ontladen.
Het ligt voor de hand dat de tijdsduur t2 evenredig is met de grootte van de ingangsspanning. De ontlaadstroom, geleverd door de referentie, is immers constant en de ontlaadtijd tot nul wordt verder alleen maar bepaald door de grootte van de spanning na t1. Het volstaat dus gedurende t2 een teller te sturen met pulsen van een bepaalde frequentie en de tellerinhoud na t2 op een uitlezing zichtbaar te maken. Op het display verschijnt dan de numerieke waarde van de ingangsspanning.
 |
| Het principe van de dual slope omzetting. (© 2021 Jos Verstraten) |
Dual-slope omzetters met auto-zero
Het beschreven principe wordt in de praktijk uitgebreid met een zogenaamde 'auto-zero'-fase. In deze fase wordt de eventuele offset van de toegepaste op-amp's automatisch gecompenseerd. Het gevolg is dat het display écht op nul komt te staan als u de analoge ingang op 0,00 V zet. Bovendien wordt het systeem zó uitgebreid dat u er zowel negatieve als positieve spanningen mee kunt meten.
Door Texas Instruments werd een beroemd IC-paar ontwikkeld, dat volgens dit principe werkte: de TL500CN en de TL502CN. Op dit blog wordt dat auto-zero systeem van dual-slope ADC uitgebreid beschreven aan de hand van deze chip's, lees Nabouw: 4,5 decade paneelmeter.
De ICL7106, ICL7107, ICL7129, ICL7136 en ICL7137
Dual-slope ADC chip's met 'auto-zero' zijn nog steeds heel actueel en voor een paar euro te koop. Als u zélf digitale meters wilt ontwerpen kan dat met de in de titel van deze paragraaf genoemde IC's die door diverse fabrikanten zoals Maxim de markt worden gebracht en ook in de Nederlandse onderdelenhandel goed te koop zijn. De chip's zijn zowel leverbaar voor rechtstreekse aansturing van LED-display's als voor aansturing van LCD-display's.
Bij AliExpress kunt u bijvoorbeeld het onderstaand volledig 3½ digit kitje rond de ICL7107 bestellen voor slechts € 3,37! Dat kitje bevat de print, het IC, vier LED-display's, een display-venstertje en de noodzakelijke weerstanden en condensatoren.
Met de ICL7129 kunt u zelfs gemakkelijk een 4½ digit digitale meter ontwerpen. Deze chip is bij 'Electronica Onderdelen Online' te koop voor € 7,50.
Het beschreven principe wordt in de praktijk uitgebreid met een zogenaamde 'auto-zero'-fase. In deze fase wordt de eventuele offset van de toegepaste op-amp's automatisch gecompenseerd. Het gevolg is dat het display écht op nul komt te staan als u de analoge ingang op 0,00 V zet. Bovendien wordt het systeem zó uitgebreid dat u er zowel negatieve als positieve spanningen mee kunt meten.
Door Texas Instruments werd een beroemd IC-paar ontwikkeld, dat volgens dit principe werkte: de TL500CN en de TL502CN. Op dit blog wordt dat auto-zero systeem van dual-slope ADC uitgebreid beschreven aan de hand van deze chip's, lees Nabouw: 4,5 decade paneelmeter.
De ICL7106, ICL7107, ICL7129, ICL7136 en ICL7137
Dual-slope ADC chip's met 'auto-zero' zijn nog steeds heel actueel en voor een paar euro te koop. Als u zélf digitale meters wilt ontwerpen kan dat met de in de titel van deze paragraaf genoemde IC's die door diverse fabrikanten zoals Maxim de markt worden gebracht en ook in de Nederlandse onderdelenhandel goed te koop zijn. De chip's zijn zowel leverbaar voor rechtstreekse aansturing van LED-display's als voor aansturing van LCD-display's.
Bij AliExpress kunt u bijvoorbeeld het onderstaand volledig 3½ digit kitje rond de ICL7107 bestellen voor slechts € 3,37! Dat kitje bevat de print, het IC, vier LED-display's, een display-venstertje en de noodzakelijke weerstanden en condensatoren.
Met de ICL7129 kunt u zelfs gemakkelijk een 4½ digit digitale meter ontwerpen. Deze chip is bij 'Electronica Onderdelen Online' te koop voor € 7,50.
 |
| Een zeer goedkoop bouwsetje rond een dual-slope ADC IC. (© AliExpress) |
De counter-type ADC (DRAC-ADC)
Het werkingsprincipe van de counter-type ADC
Dit type ADC wordt ook wel eens de 'teruggekoppelde ADC' genoemd. Als u het onderstaand blokschema bekijkt zal onmiddellijk duidelijk worden dat dit niet zonder reden is. De analoge ingangsspanning wordt namelijk in een comparator vergeleken met een stapspanning die afkomstig is van een in de schakeling aanwezige digitaal naar analoog omzetter DAC. Deze DAC wordt gestuurd uit de uitgangen van de ADC. Als de trapspanning gelijk wordt aan de analoge ingangsspanning is de digitale code op de uitgangen een zo goed mogelijke binaire gewichtsbenadering van de analoge ingangsspanning.
Klinkt dit verhaal u een beetje bekend in de oren? Het werkingsprincipe lijkt inderdaad erg veel op dat van de ramp-and-compare ADC, zij het dat de zaagtand nu digitaal wordt gegenereerd en een trapvormige benadering is van een ideale zaagtand. Vandaar dat in sommige bronnen deze ADC ook wel eens DRAC-ADC word genoemd.
Uit dit werkingsprincipe volgt dat deze schakelingen een parallel uitgevoerde binaire digitale code op hun uitgangen genereren. Een acht bit brede counter-type ADC heeft dus acht uitgangen, meestal gecodeerd van Qa tot en met Qh. Hierbij staat Qa voor het LSB en Qh voor het MSB.
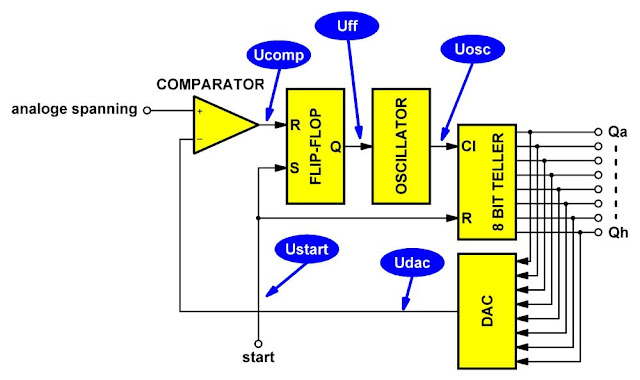 |
| Het blokschema van een counter-type ADC. (© 2021 Jos Verstraten) |
De werking van de schakeling
De werking van de schakeling wordt toegelicht aan de hand van de grafieken in de onderstaande figuur. Een omzettingscyclus start door het aanleggen van een START-puls op de gelijknamige ingang. Hierdoor wordt de flip-flop geset en de teller gereset. Alle acht uitgangen van de schakeling gaan naar 'L'. Doordat de uitgangscode 'L-L-L-L-L-L-L-L' wordt zal de analoge uitgangsspanning van de digitaal naar analoog omzetter naar 0 V gaan. Het gevolg is dat deze spanning in ieder geval kleiner is dan de waarde van de analoge ingangsspanning. De uitgang van de comparator wordt 'H'. De hoge Q-uitgang van de flip-flop start de ingebouwde oscillator. Hoewel deze schakeling begint met het leveren van pulsen aan de teller zal deze schakeling nog niet gaan tellen. Dat gebeurt pas als de START-puls wegvalt en de RESET van de teller wordt vrijgegeven. De acht uitgangen van de teller doorlopen de normale binaire code.
Het gevolg is dat de uitgangsspanning van de DAC trapvormig zal stijgen. Omdat iedere codewijziging overeen komt met een verhoging van het gewicht met één bit, zal de uitgangsspanning van de DAC steeds bij iedere klokpuls met de stapgrootte van de DAC stijgen. Dit proces gaat verder tot de uitgangsspanning van de DAC gelijk wordt aan de ingangsspanning.

Op dat moment (t3) klapt de comparator om. De 'H' naar 'L' uitgangspuls op de uitgang van de comparator reset de flip-flop. De oscillator wordt daardoor uitgeschakeld, het systeem blijft stabiel in de toestand waarbij beide analoge spanningen aan elkaar gelijk zijn.
Na het tijdsverloop t1/t3 staat er dus op de uitgangen van de schakeling een digitale code waarvan de som van de gewichten overeen komt met de grootte van de ingangsspanning. Het zal duidelijk zijn dat er bij praktische schakelingen na de teller nog een bufferregister volgt waarin de digitale code wordt opgeslagen totdat de volgende omzetting voltooid is. Op deze manier wordt voorkomen dat het telproces op de uitgangen te volgen is. Bovendien staat dan een serie codes op de uitgangen van het bufferregister die het verloop van de ingangsspanning volgt, zonder dat deze serie codes verstoord wordt door het telproces zélf.
 |
De werking van een counter-type ADC. (© 2021 Jos Verstraten) |
Eigenschappen van de counter-type ADC
Een dergelijke ADC kan zeer goedkoop worden geïntegreerd in één chip. Het grote nadeel van de schakeling is echter dat zij zeer traag werkt. Bij iedere cyclus moet de comparerende spanning uit de DAC immers weer van nul af worden opgebouwd. Een counter-type ADC is echter wél ideaal voor het inlezen van langzaam variërende meetgrootheden in het geheugen van een computer. Dan speelt immers de trage omzettingssnelheid geen grote rol. Vanwege de START en EINDE CONVERSIE signalen die uit de schakeling afgeleid kunnen worden, is een counter-type ADC een ideale partner voor een computerbus.
De tracking ADC
Het principe van de schakeling
De tracking ADC is een verfijning van de counter-type ADC. De belangrijkste verbetering is het verhogen van de omzettingssnelheid. Dat is een gevolg van het feit dat de digitale code op de uitgangen het verloop van de analoge ingangsspanning als het ware van cyclus tot cyclus volgt. Er wordt dus niet na iedere cyclus gereset. De normale op-teller van de counter-type ADC wordt vervangen door een op/neer-teller. Daalt de analoge ingangsspanning, dan wordt de teller in de neer-modus gestuurd, zodat het gewicht van de digitale code daalt totdat dit weer gelijk is aan de nieuwe waarde van de ingangsspanning.
Stijgt de ingangsspanning weer, dan gaat de teller naar de op-modus, zodat het gewicht van de digitale code zich snel aanpast aan de stijgende ingangsspanning.
Het blokschema van een tracking ADC
In de onderstaande figuur ziet u het tot het minimale vereenvoudigde blokschema van een tracking ADC. Bij het inschakelen van de voedingsspanning is de teller gereset. De uitgangscode is dan 'L-L-L-L-L-L-L-L'. De DAC levert 0 V aan de comparator. De uitgangsspanning van de comparator stuurt de op/neer-teller in de op-modus. De schakeling werkt op dit moment als een counter-type ADC.
Als de uitgangsspanning van de DAC groter wordt dan de ingangsspanning klapt de comparator om. De op/neer-teller wordt nu in de neer-modus gestuurd. Het gevolg is dat de uitgangsspanning van de DAC iets lager wordt en de neerwaartse richting van de ingangsspanning volgt.
Als de ingangsspanning stabiel blijft zal de comparator steeds omklappen van de ene naar de andere toestand. De teller wordt dus voortdurend van op- naar neer-tellen gestuurd. Op deze manier zal de uitgangscode steeds met één bit oscilleren rond de waarde van de ingangsspanning.
Wat is een successive approximation register?
Het blokschema van een SAR-ADC is identiek aan dat van een tracking ADC. Het enige verschil is dat de op/neer-teller nu wordt vervangen door een speciaal register, een zogenaamd SAR.
SAR staat voor 'Successive Approximation Register', vrij vertaald 'register dat zorgt voor opeenvolgende benadering'. Dit register zorgt ervoor dat de uitgangsspanning van de DAC zo snel mogelijk gelijk wordt aan de ingangsspanning.
De werking van een SAR-ADC kan het best toegelicht worden aan de hand van een alledaags voorbeeld. Stel dat u het gewicht van een voorwerp moet bepalen met een apothekersbalans. U legt het voorwerp in de ene schaal, de bedoeling is dat u in de andere schaal gewichten legt tot de balans in evenwicht is. Als u volgens het principe van de counter-type ADC gaat werken doet u niets anders dan gewichtjes van één gram op de schaal leggen tot de balans omslaat. Nadien gaat u het gewicht van het voorwerp bepalen door het aantal gewichtjes van één gram op te tellen. Als u volgens het systeem van de SAR-ADC gaat werken zet u eerst een gewicht van één kilogram in de schaal. Slaat de balans dan door, dan verwijdert u het gewicht en vervangt het door een gewicht van 500 gram. Is dit te weinig, dan vult u dit gewicht aan met een van 250 gram. Slaat de balans dan weer door, dan wordt dit tweede gewicht verwijderd en vervangen door een van 125 gram. Op deze manier kunt u heel snel het gewicht van het voorwerp bepalen.
Een SAR ADC werkt op precies dezelfde manier.
Het blokschema en de timing van een SAR-ADC
Zoals reeds geschreven is het blokschema van een SAR-ADC exact gelijk aan dat van een tracking ADC en dat publiceren wij dus niet opnieuw. De timing is uiteraard anders en weergegeven in de onderstaande figuur. Voor de eenvoud wordt hierbij gewerkt met een vijf bit brede SAR. In de praktijk zult u uiteraard dergelijke lage resoluties niet aantreffen, maar begint men te werken met minstens acht bit.
Na de eerste klokpuls (t1) maakt de SAR het hoogste bit Qe 'H'. De DAC wekt een analoge spanning op gelijkwaardig aan het gewicht van dit bit. Deze spanning wordt vergeleken met de ingangsspanning van de ADC. De comparator geeft een signaal 'spanning te hoog' af aan de controle-ingang van de SAR. Bij de volgende klokpuls wordt Qe weer 'L'. De uitgangsspanning van de DAC gaat naar nul en de comparator stuurt een signaal 'spanning te laag' naar de controle-ingang van de SAR. Bij de volgende klokpuls wordt het op een na hoogste bit Qd 'H' gemaakt. De uitgangsspanning van de DAC is nog steeds kleiner dan de ingangsspanning, de SAR krijgt van de comparator een signaal 'spanning te klein'. Bij de volgende klokpuls wordt nu ook het derde hoogste bit Qc 'H' gemaakt. De DAC levert de analoge uitgangsspanning die overeen komt met het digitale gewicht van de twee hoge bits aan de comparator. Nu is deze spanning echter groter dan de ingangsspanning. Bij de volgende klokpuls wordt Qc weer 'L' gemaakt, het signaal 'spanning te laag' zorgt ervoor dat bij de volgende klokpuls Qb 'H' wordt.
Op deze manier tast de SAR in snel tempo alle combinaties van MSB naar LSB af, tot een evenwicht is gevonden waarbij de uitgangscode oscilleert rond de waarde van de ingangsspanning.
Een zeer snelle ADC
Alle tot nu toe besproken analoog naar digitaal omzetters hebben één basiseigenschap gemeen. De om te zetten analoge ingangsspanning wordt in een comparator vergeleken met een door de schakeling zelf gegenereerde analoge spanning. Op het moment dat deze intern gegenereerde analoge spanning gelijk wordt aan de om te zetten analoge ingangsspanning stopt het proces en kunt u de binaire code op de uitgangen aflezen. Het omzetten van de ingangsspanning in een daarmee overeenkomende binaire code duurt dus een bepaalde tijd die men de cyclus- of conversietijd van de ADC noemt.
Hoewel men er in geslaagd is zeer snelle ADC-schakelingen te maken op basis van de beschreven principes, heeft men toch gezocht naar een geheel andere benadering voor het omzetten van een analoge spanning in een digitale code.
Dit principe staat bekend onder de naam 'one step flash ADC' en werkt in principe traagheidsloos. De binaire code op de uitgangen van de ADC volgt zonder vertraging de waarde van de analoge spanning op de ingang. Vandaar dat deze ADC ook wel 'direct conversion ADC' wordt genoemd.
Het principe van de one step flash ADC
Het basisschema van een 8 bit brede one step flash ADC is getekend in de onderstaande figuur. Een 8 bit binaire code heeft 256 mogelijke verschillende samenstellingen, van 'L-L-L-L-L-L-L-L '(0) tot en met 'H-H-H-H-H-H-H-H' (255). Het is dus mogelijk een analoge spanning in 256 stappen te digitaliseren. De schakeling bestaat dan ook uit 255 comparatoren, die de ingangsspanning vergelijken met even zoveel referentiespanningen. Deze spanningen ontstaan op de knooppunten van 255 in serie geschakelde volledig identieke weerstanden. De serieschakeling van de weerstanden wordt gevoed tussen de massa en een stabiele referentiespanning Uref. In de meeste gevallen is deze referentiespanning in de one step flash omzetter ingebouwd.
De werking van de schakeling volgt uit de grafieken die u rechts in de afbeelding ziet. Als de ingangsspanning gelijk is aan nul zullen alle comparatoren een hoge uitgang hebben. De ingangsspanning gaat immers via een bufferversterker naar de inverterende ingangen van alle 255 comparatoren. De niet-inverterende ingangen zijn verbonden met de knooppunten van de weerstandsdeler en staan dus op positieve spanningen. Naarmate de ingangsspanning groter wordt zullen er meer comparator-uitgangen omschakelen van 'H' naar 'L'. Als de ingangsspanning gelijk wordt aan de referentie-spanning zullen alle comparatoren een lage uitgang hebben. Deze 256 combinaties van hoge en lage comparator-uitgangen, die ieder overeen komen met een welbepaalde grootte van de ingangsspanning, worden vervolgens in een logisch netwerk omgezet in een acht bit binaire code.
Geen klok noodzakelijk?
Uit de bespreking van het fundamentele principe van one step flash omzetters volgt onmiddellijk dat deze omzetters in theorie traagheidsloos werken en dus ook niet gestuurd moeten worden met een kloksignaal. Iedere wijziging van de grootte van de analoge ingangsspanning heeft onmiddellijk een andere combinatie in de uitgangscode van de comparatoren tot gevolg en dus ook een nieuwe binaire code. De enige vertragingen die in de praktijk opgetreden zijn de onvermijdelijke traagheden in de werking van de comparatoren en de code-omzetter. Deze schakel-vertragingen bedragen slechts enige nanoseconden en one step flash converters werken dan ook tot in het GHz-gebied.
Het zal echter duidelijk zijn dat het technologisch zeer moeilijk is 255 comparatoren, niet bepaald eenvoudige schakelingen, op een chip te integreren. Comparatoren die bovendien volstrekt identieke eigenschappen (offset!) moeten hebben.
De one step flash-omzetters zijn dan ook zeer duur en vandaar dat u dit principe hoofdzakelijk aantreft in ADC's met een resolutie van slechts 4 of 6 bits. Het aantal noodzakelijke comparatoren is dan immers slechts 16 of 64, hetgeen technologisch veel minder strenge eisen aan het chip-ontwerp stelt.
Het principe van de schakeling
Een belangrijke reductie van het aantal noodzakelijke comparatoren ontstaat als u gebruik maakt van het two-step principe. De principiële werking is getekend in de onderstaande figuur. De totale resolutie van 8 bit wordt opgedeeld in twee zones, die ieder 4 bit breed zijn.
U hebt dan slechts twee 4 bit one step flash omzetters nodig en dus 2 x 16 is 32 comparatoren.
De analoge ingangsspanning wordt in de bovenste one step flash ADC omgezet in een 4 bit breed binair woord. Deze vier bits vormen de vier hoogste of most significant bits (MSB) van de totale omzetting. Uit deze 4 bits wordt door middel van een geïntegreerde 4 bit DAC een analoge spanning afgeleid.
Deze spanning, die een groffe benadering van de grootte van de ingangsspanning is, wordt in een verschilversterker van de ingangsspanning afgetrokken. Het verschil wordt aangeboden aan een tweede 4 bit one step flash ADC. De vier uitgangen van dit systeem vormen de vier laagste of least significant bits (LSB) van de totale omzetting.
Het zal duidelijk zijn dat de introductie van een DAC in de signaalverwerking een grote snelheidsvermindering tot gevolg heeft. De sampling-rate van dergelijke omzetters gaat tot ongeveer 100 MHz.
(Bol.com sponsor advertentie)
Fluke 114 Multimeter

Stijgt de ingangsspanning weer, dan gaat de teller naar de op-modus, zodat het gewicht van de digitale code zich snel aanpast aan de stijgende ingangsspanning.
Het blokschema van een tracking ADC
In de onderstaande figuur ziet u het tot het minimale vereenvoudigde blokschema van een tracking ADC. Bij het inschakelen van de voedingsspanning is de teller gereset. De uitgangscode is dan 'L-L-L-L-L-L-L-L'. De DAC levert 0 V aan de comparator. De uitgangsspanning van de comparator stuurt de op/neer-teller in de op-modus. De schakeling werkt op dit moment als een counter-type ADC.
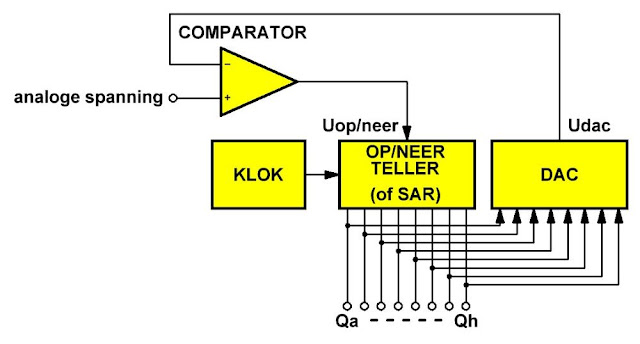 |
| Het blokschema van een tracking ADC en van een SAR-ADC. (© 2021 Jos Verstraten) |
Als de uitgangsspanning van de DAC groter wordt dan de ingangsspanning klapt de comparator om. De op/neer-teller wordt nu in de neer-modus gestuurd. Het gevolg is dat de uitgangsspanning van de DAC iets lager wordt en de neerwaartse richting van de ingangsspanning volgt.
Als de ingangsspanning stabiel blijft zal de comparator steeds omklappen van de ene naar de andere toestand. De teller wordt dus voortdurend van op- naar neer-tellen gestuurd. Op deze manier zal de uitgangscode steeds met één bit oscilleren rond de waarde van de ingangsspanning.
 |
| De werking van een tracking ADC. (© 2021 Jos Verstraten) |
De successive approximation ADC (SAR-ADC)
Wat is een successive approximation register?
Het blokschema van een SAR-ADC is identiek aan dat van een tracking ADC. Het enige verschil is dat de op/neer-teller nu wordt vervangen door een speciaal register, een zogenaamd SAR.
SAR staat voor 'Successive Approximation Register', vrij vertaald 'register dat zorgt voor opeenvolgende benadering'. Dit register zorgt ervoor dat de uitgangsspanning van de DAC zo snel mogelijk gelijk wordt aan de ingangsspanning.
De werking van een SAR-ADC kan het best toegelicht worden aan de hand van een alledaags voorbeeld. Stel dat u het gewicht van een voorwerp moet bepalen met een apothekersbalans. U legt het voorwerp in de ene schaal, de bedoeling is dat u in de andere schaal gewichten legt tot de balans in evenwicht is. Als u volgens het principe van de counter-type ADC gaat werken doet u niets anders dan gewichtjes van één gram op de schaal leggen tot de balans omslaat. Nadien gaat u het gewicht van het voorwerp bepalen door het aantal gewichtjes van één gram op te tellen. Als u volgens het systeem van de SAR-ADC gaat werken zet u eerst een gewicht van één kilogram in de schaal. Slaat de balans dan door, dan verwijdert u het gewicht en vervangt het door een gewicht van 500 gram. Is dit te weinig, dan vult u dit gewicht aan met een van 250 gram. Slaat de balans dan weer door, dan wordt dit tweede gewicht verwijderd en vervangen door een van 125 gram. Op deze manier kunt u heel snel het gewicht van het voorwerp bepalen.
Een SAR ADC werkt op precies dezelfde manier.
Het blokschema en de timing van een SAR-ADC
Zoals reeds geschreven is het blokschema van een SAR-ADC exact gelijk aan dat van een tracking ADC en dat publiceren wij dus niet opnieuw. De timing is uiteraard anders en weergegeven in de onderstaande figuur. Voor de eenvoud wordt hierbij gewerkt met een vijf bit brede SAR. In de praktijk zult u uiteraard dergelijke lage resoluties niet aantreffen, maar begint men te werken met minstens acht bit.
Na de eerste klokpuls (t1) maakt de SAR het hoogste bit Qe 'H'. De DAC wekt een analoge spanning op gelijkwaardig aan het gewicht van dit bit. Deze spanning wordt vergeleken met de ingangsspanning van de ADC. De comparator geeft een signaal 'spanning te hoog' af aan de controle-ingang van de SAR. Bij de volgende klokpuls wordt Qe weer 'L'. De uitgangsspanning van de DAC gaat naar nul en de comparator stuurt een signaal 'spanning te laag' naar de controle-ingang van de SAR. Bij de volgende klokpuls wordt het op een na hoogste bit Qd 'H' gemaakt. De uitgangsspanning van de DAC is nog steeds kleiner dan de ingangsspanning, de SAR krijgt van de comparator een signaal 'spanning te klein'. Bij de volgende klokpuls wordt nu ook het derde hoogste bit Qc 'H' gemaakt. De DAC levert de analoge uitgangsspanning die overeen komt met het digitale gewicht van de twee hoge bits aan de comparator. Nu is deze spanning echter groter dan de ingangsspanning. Bij de volgende klokpuls wordt Qc weer 'L' gemaakt, het signaal 'spanning te laag' zorgt ervoor dat bij de volgende klokpuls Qb 'H' wordt.
Op deze manier tast de SAR in snel tempo alle combinaties van MSB naar LSB af, tot een evenwicht is gevonden waarbij de uitgangscode oscilleert rond de waarde van de ingangsspanning.
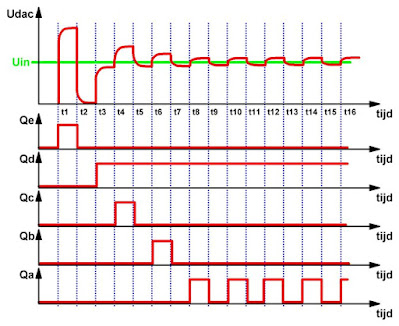 |
| De werking van een SAR-ADC. (© 2021 Jos Verstraten) |
De one step flash ADC
Een zeer snelle ADC
Alle tot nu toe besproken analoog naar digitaal omzetters hebben één basiseigenschap gemeen. De om te zetten analoge ingangsspanning wordt in een comparator vergeleken met een door de schakeling zelf gegenereerde analoge spanning. Op het moment dat deze intern gegenereerde analoge spanning gelijk wordt aan de om te zetten analoge ingangsspanning stopt het proces en kunt u de binaire code op de uitgangen aflezen. Het omzetten van de ingangsspanning in een daarmee overeenkomende binaire code duurt dus een bepaalde tijd die men de cyclus- of conversietijd van de ADC noemt.
Hoewel men er in geslaagd is zeer snelle ADC-schakelingen te maken op basis van de beschreven principes, heeft men toch gezocht naar een geheel andere benadering voor het omzetten van een analoge spanning in een digitale code.
Dit principe staat bekend onder de naam 'one step flash ADC' en werkt in principe traagheidsloos. De binaire code op de uitgangen van de ADC volgt zonder vertraging de waarde van de analoge spanning op de ingang. Vandaar dat deze ADC ook wel 'direct conversion ADC' wordt genoemd.
Het principe van de one step flash ADC
Het basisschema van een 8 bit brede one step flash ADC is getekend in de onderstaande figuur. Een 8 bit binaire code heeft 256 mogelijke verschillende samenstellingen, van 'L-L-L-L-L-L-L-L '(0) tot en met 'H-H-H-H-H-H-H-H' (255). Het is dus mogelijk een analoge spanning in 256 stappen te digitaliseren. De schakeling bestaat dan ook uit 255 comparatoren, die de ingangsspanning vergelijken met even zoveel referentiespanningen. Deze spanningen ontstaan op de knooppunten van 255 in serie geschakelde volledig identieke weerstanden. De serieschakeling van de weerstanden wordt gevoed tussen de massa en een stabiele referentiespanning Uref. In de meeste gevallen is deze referentiespanning in de one step flash omzetter ingebouwd.
De werking van de schakeling volgt uit de grafieken die u rechts in de afbeelding ziet. Als de ingangsspanning gelijk is aan nul zullen alle comparatoren een hoge uitgang hebben. De ingangsspanning gaat immers via een bufferversterker naar de inverterende ingangen van alle 255 comparatoren. De niet-inverterende ingangen zijn verbonden met de knooppunten van de weerstandsdeler en staan dus op positieve spanningen. Naarmate de ingangsspanning groter wordt zullen er meer comparator-uitgangen omschakelen van 'H' naar 'L'. Als de ingangsspanning gelijk wordt aan de referentie-spanning zullen alle comparatoren een lage uitgang hebben. Deze 256 combinaties van hoge en lage comparator-uitgangen, die ieder overeen komen met een welbepaalde grootte van de ingangsspanning, worden vervolgens in een logisch netwerk omgezet in een acht bit binaire code.
 |
| Blokschema en werking van een one step flash ADC. (© 2021 Jos Verstraten) |
Geen klok noodzakelijk?
Uit de bespreking van het fundamentele principe van one step flash omzetters volgt onmiddellijk dat deze omzetters in theorie traagheidsloos werken en dus ook niet gestuurd moeten worden met een kloksignaal. Iedere wijziging van de grootte van de analoge ingangsspanning heeft onmiddellijk een andere combinatie in de uitgangscode van de comparatoren tot gevolg en dus ook een nieuwe binaire code. De enige vertragingen die in de praktijk opgetreden zijn de onvermijdelijke traagheden in de werking van de comparatoren en de code-omzetter. Deze schakel-vertragingen bedragen slechts enige nanoseconden en one step flash converters werken dan ook tot in het GHz-gebied.
Het zal echter duidelijk zijn dat het technologisch zeer moeilijk is 255 comparatoren, niet bepaald eenvoudige schakelingen, op een chip te integreren. Comparatoren die bovendien volstrekt identieke eigenschappen (offset!) moeten hebben.
De one step flash-omzetters zijn dan ook zeer duur en vandaar dat u dit principe hoofdzakelijk aantreft in ADC's met een resolutie van slechts 4 of 6 bits. Het aantal noodzakelijke comparatoren is dan immers slechts 16 of 64, hetgeen technologisch veel minder strenge eisen aan het chip-ontwerp stelt.
De two step flash ADC
Het principe van de schakeling
Een belangrijke reductie van het aantal noodzakelijke comparatoren ontstaat als u gebruik maakt van het two-step principe. De principiële werking is getekend in de onderstaande figuur. De totale resolutie van 8 bit wordt opgedeeld in twee zones, die ieder 4 bit breed zijn.
U hebt dan slechts twee 4 bit one step flash omzetters nodig en dus 2 x 16 is 32 comparatoren.
De analoge ingangsspanning wordt in de bovenste one step flash ADC omgezet in een 4 bit breed binair woord. Deze vier bits vormen de vier hoogste of most significant bits (MSB) van de totale omzetting. Uit deze 4 bits wordt door middel van een geïntegreerde 4 bit DAC een analoge spanning afgeleid.
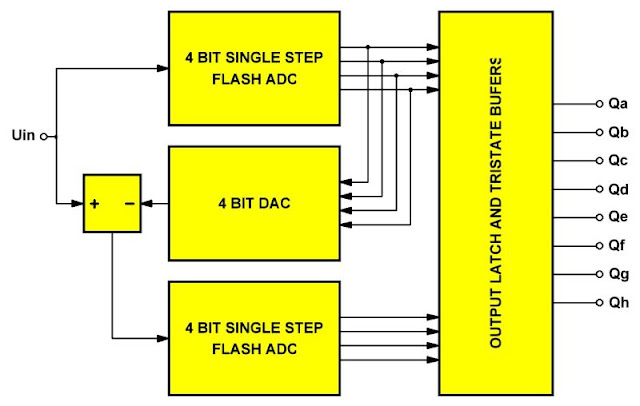 |
Het blokschema van een two step flash ADC. (© 2021 Jos Verstraten) |
Deze spanning, die een groffe benadering van de grootte van de ingangsspanning is, wordt in een verschilversterker van de ingangsspanning afgetrokken. Het verschil wordt aangeboden aan een tweede 4 bit one step flash ADC. De vier uitgangen van dit systeem vormen de vier laagste of least significant bits (LSB) van de totale omzetting.
Het zal duidelijk zijn dat de introductie van een DAC in de signaalverwerking een grote snelheidsvermindering tot gevolg heeft. De sampling-rate van dergelijke omzetters gaat tot ongeveer 100 MHz.
Fluke 114 Multimeter
