|
U kunt het laden van een condensator beïnvloeden door een weerstand in serie met de condensator op te nemen. Hierdoor ontstaat een RC-kring met speciale eigenschappen, die men integrator of differentiator noemt.
|
De RC-laadkring
Laden van een condensator via een weerstand
Stel dat u, zoals getekend in onderstaande figuur, een condensator C en een weerstand R via een schakelaar S in serie aansluit op een spanningsbron U. U sluit de schakelaar en onderzoekt wat er in de kring gebeurt.
 |
| De RC-laadkring, aangesloten op een spanningsbron. (© 2017 Jos Verstraten) |
Op het moment dat u de schakelaar S sluit is de spanning over de condensator uiteraard gelijk aan nul. Over de weerstand staat op dit moment de volle spanning U van de spanningsbron. Er gaat nu een laadstroom door de kring vloeien, waarvan de grootte in eerste instantie bepaald wordt door de waarde van de weerstand R. Het gevolg is dat er lading wordt getransporteerd van de spanningsbron U naar de condensator. Deze lading bouwt een spanning Uc op over de condensator met de getekende polariteit. Er staan dan twee bronnen in serie, namelijk U en Uc, die tegengestelde polariteit hebben. Het gevolg is dat de spanning over de weerstand daalt. Maar als er over een weerstand een spanningsdaling optreedt, kan dat niets anders betekenen dan dat ook de stroom daalt. De laadstroom van de condensator wordt dus kleiner, met als gevolg dat er per tijdseenheid minder lading naar van de bron naar de condensator getransporteerd wordt. Naarmate het proces vordert, zal de stroom door de kring steeds kleiner worden en de spanning over de condensator steeds minder snel stijgen.
| FORMULES IN DIT ARTIKEL |
|---|
| VERMENIGVULDIGEN:
Het vermenigvuldigingsteken wordt voorgesteld door een bullet tussen de factoren: a • b = c DELEN: Het gedeeld door teken wordt voorgesteld door een schuine streep: a / b = c |
De condensatorspanning in een grafiek
Als u een grafiekje opstelt van het spanningsverloop over de condensator in functie van de tijd, ontstaat het typische beeld van onderstaande figuur. Op t = 0 is de condensatorspanning 0 V. Eerst gaat de spanning heel erg snel stijgen. Naarmate de tijd verstrijkt gaat de spanning steeds minder snel stijgen. Na een heel lange tijd zal de spanning over de condensator precies gelijk zijn aan de spanning van de bron. De stroom in de kring wordt dan nul, het systeem is in rust. De condensator is volledig opgeladen.
 |
| Het verloop van de spanning over de condensator. (© 2017 Jos Verstraten) |
Het begrip tijdconstante
Het product van weerstand en condensator
De snelheid waarmee een en ander gebeurt is niet alleen afhankelijk van de waarde van de weerstand, maar ook van de waarde van de condensator. Immers, de spanning over een condensator wordt gegeven door de uitdrukking:
U = Q / C
Hoe groter de condensator, hoe minder snel de spanning zal toenemen. Dat dubbele verband wordt uitgedrukt door de tijdconstante van de RC-kring. De tijdconstante wordt voorgesteld door de Griekse letter τ, uitgesproken als 'tau' en gelijk aan:
τ = R • C
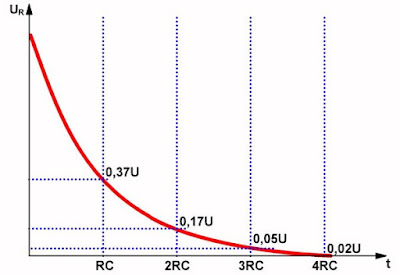
De definitie van deze tijdconstante is als volgt: de tijdconstante τ is de tijd die nodig is om een condensator via een weerstand op te laden tot een spanning, die gelijk is aan 63 % van de waarde U van de spanningsbron. Zoals uit de grafiek blijkt is de condensatorspanning na 4 • τ gestegen tot 98 % van de bronspanning.
De eenheid van τ
Uit de definitie van de tijdconstante volgt iets vreemds, τ is een tijd en moet dus als eenheid de seconde hebben. Maar τ is gelijk aan het product van weerstand en capaciteit. Hoe kan dit product de seconde als eenheid hebben? Toch kan dit gemakkelijk aangetoond worden.
De spanning over een condensator wordt gegeven door:
U = Q / C
Uit de definitie van lading, het vloeien van stroom gedurende een bepaalde tijd, kunt u afleiden:
Q = I • t
Dus:
U = [I • t] / C
Als u C van links naar rechts verplaatst en U van rechts naar links ontstaat:
C = [I • t] / U
Maar u weet als kenner van de wet van Ohm:
U = I • R
Dit is ook te schrijven als:
1 • U = I • R
Door het verwisselen van plaats van U en R ontstaat:
I / U = 1 / R
Dus:
C = t / R
Vul nu deze waarde van C in de formule van T in:
τ = R • [t / R]
U kunt R in teller en noemer wegstrepen:
τ = t
De tijdconstante τ is dus inderdaad niets anders dan een tijd.
Het belang van de tijdconstante
De tijdconstante τ van een RC-kring is een zeer belangrijke en praktische parameter in de elektronica. Stel bijvoorbeeld dat u ergens in een schakeling een tijdvertraging van één seconde moet realiseren tussen een eerste en een tweede verschijnsel. Dat kan door gebruik te maken van de schakeling die in onderstaande figuur getekend is.
 |
| Een praktische toepassing waaruit het belang van de tijdconstante τ blijkt. (© 2017 Jos Verstraten) |
R = τ / C
De RC-ontlaadkring
Het ontladen van een geladen condensator
Stel dat u een geladen condensator C door middel van een schakelaar S kortsluit over een weerstand R, zoals getekend in onderstaande figuur. U stelt de laadspanning van de condensator gelijk aan Uc. Op het moment dat u de schakelaar sluit zal er een stroom door de kring gaan vloeien. Deze stroom heeft tot gevolg dat de in de opgeslagen condensator verzamelde lading afvloeit. De spanning Uc over de condensator gaat dus dalen.
 |
| Het ontladen van een geladen condensator C over een weerstand R. (© 2017 Jos Verstraten) |
Ook nu kunt u een grafiekje opstellen waarin het verband wordt gegeven tussen het verloop van de condensatorspanning Uc en de tijd. Dit grafiekje is getekend in onderstaande figuur. Het zal geen verbazing wekken dat de condensatorspanning in het begin vrij snel daalt. De ontlaadstroom is dan immers groot. Naarmate echter de spanning daalt zal er steeds minder stroom door de weerstand vloeien en zal de spanning over de condensator dus steeds trager dalen. Maar hoe traag dat ook gaat, uiteindelijk zal de condensatorspanning gelijk worden aan 0 V. De condensator is dan volledig ontladen. U kunt vaststellen dat de condensatorspanning tot 37 % van zijn beginwaarde Uc is gedaald na één tijdconstante τ. Na 4 • τ staat er nog maar 2 % van de beginspanning over het onderdeel.
 |
| De ontlaadcurve van een condensator in een RC-kring. (© 2017 Jos Verstraten) |
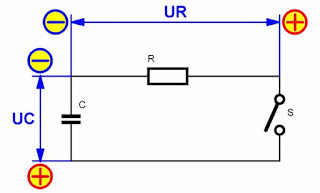
De spanning over de weerstand
Bij het laden van de condensator
Tot nu toe is het spanningsverloop over de condensator als belangrijke grootheid gebruikt. Maar natuurlijk zal de spanning over de weerstand ook een bepaald verloop hebben. Het zal, bij het laden uit een spanningsbron, duidelijk zijn dat de spanning over de weerstand op ieder moment van het proces gelijk is aan de constante bronspanning minus de stijgende spanning over de condensator. Dat is gemakkelijk in te zien, maar u kunt dat met de wetten van Thévenin ook bewijzen.
In het begin van de lading, als de condensatorspanning nog 0 V is, is de spanning over de weerstand gelijk aan de bronspanning. Na 1 • τ is de spanning over de weerstand gedaald tot 37 % van de bronspanning. Het grafisch verloop in functie van de tijd is getekend in onderstaande figuur.
 |
| Het verloop van de spanning over de weerstand bij de RC-laadkring. (© 2017 Jos Verstraten) |
Integratoren en differentiatoren
Praktische schakelingen met de RC-kring
Een RC-kring zult u vaak te hulp roepen als u iets met een pulsspanning in functie van de tijd moet doen. De twee schakelingen die u het vaakst zult toepassen zijn de integrator en de differentiator. Zowel integrator als differentiator hebben talloze toepassingen in de praktische elektronica, en dan voornamelijk in tijdschakelingen. Onderzoek maar eens twintig nabouwschakelingen die iets doen met tijd en in de meeste gevallen zult u op tal van plaatsen integratoren en differentiatoren ontdekken!
De integrator
Deze schakeling is in onderstaande figuur getekend. Het is niets anders dan de reeds bekende RC-kring, waar de spanning over de condensator als uitgang wordt genomen. Als u een smalle spanningspuls op de ingang legt zal deze smalle puls door de condensator breder gemaakt worden. Men spreekt van een integrator of integrerende schakeling.
 |
| De werking van de integrator grafisch toegelicht. (© 2017 Jos Verstraten) |
In het onderstaande schema zijn weerstand en condensator van plaats verwisseld. De spanning over de weerstand is nu de uitgangsspanning. Als u dezelfde smalle puls aan de schakeling aanbiedt stelt u vast dat er over de weerstand twee veel smallere, naaldvormige pulsen ontstaat. De eerste is positief, de tweede is even groot en breed en negatief. De schakeling kan dus gebruikt worden als pulsversmaller. Uiteraard is de breedte van de naaldpulsen afhankelijk van de waarde van τ en dus van de waarde van de toegepaste onderdelen. Men spreekt van een differentiator of differentiërende schakeling.
 |
| De werking van de differentiator grafisch toegelicht. (© 2017 Jos Verstraten) |
|
|
