|
Als u de terugkoppelingsweerstand van een op-amp vervangt door een niet-lineair element zoals een diode, gaat het lineaire verband tussen de in- en uitgangsspanning verloren. De versterkingsfactor van de schakeling wordt afhankelijk van de grootte van de ingangsspanning. |
Wat betekent niet-lineariteit?
Weerstanden zorgen voor een lineaire werking
Tot nu toe hebt u steeds een weerstand als terugkoppeling tussen de uit- en ingangen van de op-amp aangebracht. Zo'n terugkoppeling noemt men lineair, omdat hij dezelfde terugkoppelingsfactor oplevert voor gelijk welke spanningsgrootte aan in- of uitgang. Een weerstand van 1 kΩ is immers een weerstand van 1 kΩ. Het gevolg is dat ook de versterkingsfactor van de schakeling rond de op-amp onafhankelijk is van de grootte van de spanningen. Heeft uw schakeling een versterking van 10 en legt u aan de ingang een spanning van 1 V, dan zal op de uitgang een spanning van 10 V verschijnen. Verlaagt u de spanning op de ingang tot 0,1 V, dan zal de spanning op de uitgang ook een factor tien kleiner worden, dus dalen tot 1 V.
De diode als niet-lineair onderdeel
Nu bestaan er echter ook niet-lineaire componenten. Dat zijn componenten waarvan de weerstandswaarde afhankelijk is van de grootte van de spanning over het onderdeel, of van de grootte van de stroom door het onderdeel. De gewone siliciumdiode, zoals de bekende 1N4148, is een typisch voorbeeld van een niet-lineair element. Dat kunt u afleiden uit de stroom/spanning-grafiek, getekend in onderstaande figuur. Deze grafiek geeft het verband tussen de spanning over de diode en de stroom die als gevolg van het aanleggen van deze spanning door het onderdeel gaat lopen. Dit verband is niet lineair. Als de spanning klein is (ongeveer 0,1 V) dan loopt er een zeer kleine stroom door de diode. Als u de spanning verdubbelt stelt u vast dat de stroom meer dan verdubbelt. Zou u een spanning van 1 V over de diode zetten, dan zou u vaststellen dat de stroom zeker een factor 1.000 groter zou worden, waardoor het onderdeel onmiddellijk zou smelten.
 |
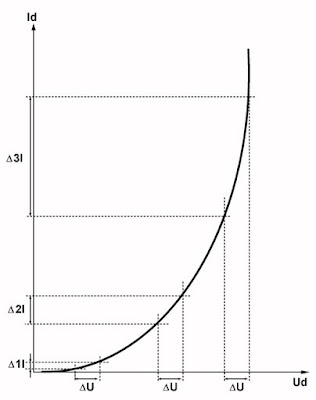| De stroom/spanning-karakteristiek van een ordinaire siliciumdiode zoals de 1N4148. (© 2017 Jos Verstraten) |
Uit de samenhang tussen spanning en stroom kunt u de inwendige weerstand van een onderdeel afleiden. De weerstand wordt immers door de wet van Ohm gegeven als het resultaat van spanning gedeeld door stroom. In de grafiek kunt u op de as van de spanning op drie plaatsen een gelijk spanningsgebied ΔU afmeten. U kunt dan op de as van de stroom aflezen hoeveel de stroom door de diode varieert als u de spanning met ΔU laat stijgen. Hieruit blijkt dat de stroomvariatie Δ1I veel kleiner is dan Δ3I.
Uit de wet van Ohm volgt dat de inwendige weerstand van de diode wordt gegeven door:
Ri = ΔU / ΔI
Een kleine stroomvariatie voor een bepaalde spanningsvariatie ΔU komt dus overeen met een hoge inwendige weerstand. Een grote stroomvariatie voor dezelfde spanningsvariatie ΔU komt overeen met een lage inwendige weerstand.
Conclusie
Als u de spanning over een diode laten stijgen van 0 V tot 0,6 V, varieert de inwendige weerstand van bijna oneindig tot bijna nul. Van deze eigenschap kunt u gebruik maken voor het opbouwen van een niet-lineaire terugkoppeling bij een op-amp.
Het schema
Het schema is getekend in onderstaande figuur. De ingangsspanning wordt aangeboden aan de inverterende ingang. Tussen deze ingang en de uitgang is een netwerkje opgenomen, opgebouwd uit een vaste weerstand R3 en vier dioden. U kunt opmerken dat het schema voldoet aan de basisopzet van een inverterende versterker. Een spanningsstijging op de ingang zal een spanningsdaling op de uitgang tot gevolg hebben.
 |
| Het schema van een eenvoudige niet-lineaire versterker. (© 2017 Jos Verstraten) |
Experimenteer mee met deze cursus!
U kunt de experimenten die in deze cursus worden beschreven zélf uitvoeren.
Daarvoor moet u echter eerst onze 'analoge trainer' nabouwen.
De uitgebreide beschrijving van de zelfbouw van dit apparaat treft u aan op de onderstaande link:
Hobby-lab: bouw een analoge trainer
De niet-lineaire versterker op uw experimenteerprint
Dit experiment kunt u volgens onderstaande figuur opbouwen op uw experimenteerprint.
 |
| De schakeling op uw experimenteerprint. (© 2017 Jos Verstraten) |
Wat is de invloed van de vier dioden op de werking van de inverterende versterker? Dat kunt u gaan meten en de resultaten van uw metingen in een tabel verwerken. U laat de ingangsspanning in stappen van 0,1 V stijgen en meet telkens de uitgangsspanning. Uw hebt na afloop twintig spanningen gemeten, tien aan de ingang en tien aan de uitgang, die u keurig in uw tabel hebt ingevuld. De gegevens in uw tabel zijn echter niet erg inzichtelijk. Vandaar dat u deze gegevens moet verwerken door deze om te zetten in een grafiek, zie onderstaande figuur. De horizontale as geeft de ingangsspanning, de verticale as de uitgangsspanning. In beide assen worden alleen de absolute waarden van de spanningen ingevuld, dus het minteken voor de uitgangsspanning wordt niet meegenomen. Dat de schakeling inverteert is in dit kader namelijk niet belangrijk. Het verband is, zoals te verwachten was, niet lineair. Voor kleine ingangsspanningen stijgt de uitgangsspanning lineair. Een verdubbeling van Vin heeft een verdubbeling van Vuit tot gevolg. Voor ingangsspanningen boven 0,6 V gaat dat niet meer op. De uitgangsspanning stijgt dan minder vlug voor gelijke spanningsstijgingen aan de ingang.
 |
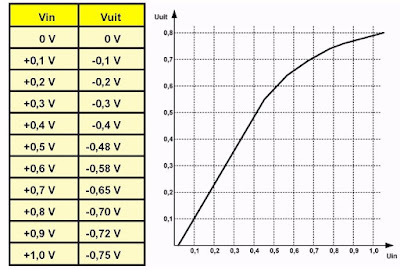| Uw meetresultaten in een tabel en in een grafiek. (© 2017 Jos Verstraten) |
Toepassing: driehoek naar sinus omvormer
Een pseudo-sinus
Als u uw verbeelding aan het werk zet, doet het grafiekje u ongetwijfeld ergens aan denken. Inderdaad, een sinusspanning verloopt ongeveer volgens hetzelfde patroon. De grafiek geeft niets anders weer dan het verloop van een kwart van de periode van een sinus. Zonder het te beseffen hebt u dus een zeer eenvoudige driehoek naar sinus omvormer gebouwd die u in principe achter de functiegenerator uit het vorige experiment 'De op-amp als functiegenerator' zou kunnen schakelen. Het volstaat op de ingang van deze schakeling een driehoek aan te sluiten met een top-tot-top waarde van 2 V om aan de uitgang een sinus te krijgen met een top-tot-top waarde van 1,5 V.
 |
| Het omzetten van een driehoek- in een sinus-spanning. (© 2017 Jos Verstraten) |
Voor kleine ingangsspanningen zijn de dioden in de terugkoppeling niet actief. De versterking van de schakeling wordt bepaald door de verhouding van R1 tot R3. Beide weerstanden zijn even groot, de versterkingsfactor is -1. Als de ingangsspanning stijgt wordt de versterking van de schakeling niet meer alleen bepaald door de weerstandsverhouding, maar ook door de dalende weerstand van de dioden. De weerstand in de terugkoppeling daalt, dus ook de versterking, dus ook de stijging van de uitgangsspanning. De uitgangsspanning wordt dus als het ware 'afgetopt', met als gevolg dat de driehoek wordt omgezet in een sinus.
Eenvoudig, maar met beperkingen
In de praktijk kleven er nogal wat bezwaren aan deze simpele driehoek naar sinus omzetter. Het belangrijkste bezwaar is de relatief hoge vervorming. De schakeling levert een sinus met minimaal 2% vervorming en dat is veel te veel om in de praktijk bruikbaar te zijn. Een tweede bezwaar is dat de goede werking van de schakeling volledig afhankelijk is van de grootte van de driehoeksspanning aan de ingang. Zou deze iets groter of iets kleiner worden, dan werkt de omzetter of niet meer, of gaat de sinusvervorming erg hoog worden. Vandaar dat men in de praktijk veel ingewikkelder schakelingen gebruikt, die echter wel op dit principe berusten. In plaats van één terugkoppeltak met vier dioden bouwt men dan een heel netwerk op met weerstanden en soms wel tientallen dioden of transistoren, die voor een zeer nauwkeurige omzetting van driehoek in sinus zorgen. Met deze schakelingen kunt u sinussen met een vervorming van enige tienden procent opwekken.
Een voorbeeld uit de praktijk
Om u een indruk te geven van de complexiteit van dergelijke schakelingen hebben wij de driehoek naar sinus omzetter in de ICL8038, een functiegenerator-IC van Intersil, in onderstaande figuur voorgesteld. De combinatie van weerstanden en dioden is nu vervangen door een ingewikkeld netwerk van weerstanden en transistoren, die echter dezelfde functie vervullen. Naarmate de driehoekvormige spanning aan de ingang stijgt, gaan steeds meer transistoren geleiden, waardoor de weerstand van het gehele netwerk afneemt en de driehoek vrij nauwkeurig in een sinus wordt omgezet.
 |
| In de ICL8038 wordt niet-lineaire schakeling toegepast voor het omzetten van een driehoek in een mooie sinus. (© Intersil) |
|
|