
|
Zelfs in dit digitale tijdperk zijn analoge filterschakelingen onmisbaar. Bij iedere ADC en iedere DAC wordt immers een analoog filter toegepast.
|
Kennismaking met analoge filterschakelingen
Definitie
Een analoog filter is een schakeling met een frequentie-afhankelijke doorlaat- of amplitude-karakteristiek. Dat wil zeggen dat de versterking of verzwakking van de schakeling afhankelijk is van de frequentie van het signaal dat u aan de ingang aanlegt.
In de onderstaande figuur is bijvoorbeeld de amplitude-karakteristiek van een banddoorlaat filter weergegeven. Alleen signalen waarvan de frequentie rond 1 kHz ligt worden door de schakeling versterkt.
 |
| Een analoog banddoorlaat filter met een centrale frequentie van 1 kHz. (© 2019 Jos Verstraten) |
Filters zijn zeer belangrijke analoge schakelingen die in ruime mate worden toegepast in tal van apparaten. In de meeste analoge apparatuur kunt u een of meerdere filters aantreffen. Met name in de audiotechniek zijn er genoeg toepassingen te verzinnen waarbij u met filtertechniek te maken krijgt. De toonregeling in een analoge audioversterker zou niet kunnen werken zonder gebruik te maken van filters. Ook analoge voorversterkers die vinyl-platen afspelen kunnen niet zonder analoge filters. Daarnaast worden analoge filters in iedere CD-speler toegepast om het herwonnen analoge signaal van de restanten van de sample-frequentie te ontdoen. In alle overige digitaal werkende audio-technieken, zoals DAT en DDC, worden vergelijkbare filtertechnieken gebruikt.
Moeilijke schakelingen
Ondanks hun belangrijkheid hebben de meeste elektronica hobbyisten echter niet veel ervaring met filters. Dat is zeer begrijpelijk, want het ontwerpen van een goed filter is niet eenvoudig en zonder een behoorlijke dosis wiskunde komt u niet ver. Bovendien bestaan er zoveel verschillende soorten en typen dat alleen specialisten een overzicht houden en weten voor welke toepassing welk filter het beste is. Met dit artikel hopen wij u een inzicht geven in deze complexe materie. Wij gaan hier niet in op praktische schakelingen, maar geven uitsluitend de noodzakelijke basiskennis die u nodig hebt om analoge filters te begrijpen. Praktische filterschakelingen komen aan de orde in diverse artikelen in het onderdeel 'Elektronische schakelingen' op dit blog.
Soorten analoge filters
Filters kunt u op verschillende manieren indelen. Een voor de hand liggende indeling is uiteraard naar de doorlaat-karakteristiek. In de praktijk kunt u vijf typen van filters onderscheiden, waarvan de doorlaat-karakteristieken in de onderstaande figuur zijn samengevat.
- Laagdoorlaat filter
Het ideale laagdoorlaat filter laat alle frequenties vanaf 0 Hz tot een bepaalde afsnijfrequentie f0 onverzwakt door. Deze f0 noemt men in het Engels de 'cutoff frequency' en deze term zult u vaak tegenkomen. Boven deze frequentie worden de signalen verzwakt, waarbij de verzwakking toeneemt naarmate de frequentie stijgt. - Hoogdoorlaat filter
Dit filter werkt tegengesteld. Alle signalen met een frequentie beneden een bepaalde afsnijwaarde worden verzwakt. Naarmate de frequentie stijgt neemt de verzwakking echter af. Alle signalen met frequenties boven de afsnijfrequentie worden onverzwakt doorgelaten. - Banddoorlaat filter
Dit filter laat alleen signalen door die frequenties hebben die tussen twee grenswaarden liggen. Afhankelijk van de samenstelling van het filter kunnen deze twee grensfrequenties dicht bij elkaar liggen (smalbandig filter) of ver uit elkaar liggen (breedbandig filter). - Bandsper filter
Het bandsper filter blokkeert alle signalen met frequenties tussen twee grenswaarden. Ook nu kunnen deze grenswaarden ver of dicht uit elkaar liggen. - Allesdoorlaat filter
Dit lijkt in eerste instantie een onzinnig filter. Alle frequenties worden namelijk onverzwakt doorgekoppeld, maar er ontstaat een faseverschuiving tussen het signaal aan de ingang en het signaal aan de uitgang.
 |
| De vijf basis filterschakelingen. (© 2019 Jos Verstraten) |
De parameters van een analoog filter
Inleiding
Net zoals ieder ander elektronisch netwerk wordt ook een analoog filter gekenmerkt en gedefinieerd door een aantal eigenschappen en specificaties. De voornaamste parameters van een analoog filter zijn:
- De amplitude- of doorlaat-karakteristiek.
- De afsnijfrequentie f0 of fc.
- De steilheid.
- De orde.
- De fase-karakteristiek.
- De Bode-plot.
- De looptijd-karakteristiek.
- De stap-respons.
De amplitude-karakteristiek Uuit = f(Uin)
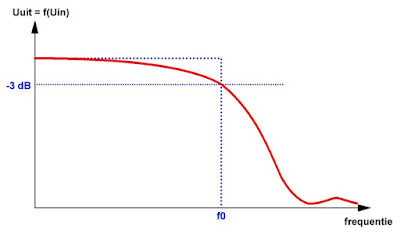
De amplitude-karakteristiek is dé belangrijkste specificatie van gelijk welk filter. In de meeste gevallen wordt de versterking of verzwakking bij verschillende frequenties uitgedrukt in dB ten opzichte van een referentie-frequentie waarbij de verzwakking of versterking wordt gelijk gesteld aan 0 dB. Een dergelijke karakteristiek van een filter is getekend in de onderstaande figuur. Let er goed op dat de horizontale frequentie-as een logaritmische schaalindeling heeft. Dat wil dus zeggen dat iedere frequentie-decade (van 1 Hz tot 10 Hz, etc.) door een even breed gebied op de as wordt voorgesteld.
Deze karakteristiek wordt ook wel eens het 'eerste Bode-diagram' genoemd.
 |
| De amplitude- of eerste Bode karakteristiek van een filter. (© 2019 Jos Verstraten) |
Uit het eerste Bode-diagram kunt u een belangrijke specificatie van een filter afleiden. Er bestaat een bepaalde frequentie waarbij de verzwakking van het filter gestegen is tot -3 dB. In de bovenstaande figuur is dit punt met dikke groene lijnen weergegeven. Deze frequentie wordt de afsnijfrequentie van het filter genoemd en wordt in de meeste gevallen voorgesteld door het symbool f0 of fc. De 'c' staat voor het Engelse 'cutoff'.
De steilheid van een filter
In principe zou een laagdoorlaat filter een scherp eerste Bode-diagram moeten hebben. Alle frequenties tot een bepaalde waarde worden onverzwakt doorgelaten, alle overige frequenties worden oneindig verzwakt. Uit de bovenstaande figuur blijkt echter dat dit in de praktijk niet het geval is. De doorlaat-karakteristiek heeft een bepaalde helling, die de steilheid van het filter wordt genoemd. Deze steilheid is een tweede belangrijke eigenschap van ieder filter.
Deze steilheid wordt uitgedrukt in dB/octaaf of dB/decade. In het eerste geval meet u de verzwakking die optreedt tussen de afsnijfrequentie f0 en de dubbele afsnijfrequentie 2 ● f0. In het tweede geval meet u de verzwakking tussen de afsnijfrequentie en de tienvoudige afsnijfrequentie. In de praktijk wordt de steilheid echter meestal uitgedrukt in dB/octaaf.
De orde van het filter
De orde van het filter heeft rechtstreeks te maken met de steilheid ervan. Hoe steiler het filter, hoe hoger de orde. Een filter van de eerste orde heeft een steilheid van 6 dB/octaaf. Een filter van de tweede orde haalt een verzwakking van 12 dB/octaaf. Iedere stijging van de steilheid met 6 dB/octaaf verhoogt de orde met de eenheid. Een vierde orde filter verzwakt dus met 24 dB/octaaf.
In de onderstaande grafiek is de amplitude-karakteristiek van een eerste orde filter vergeleken met deze van een tweede orde filter.
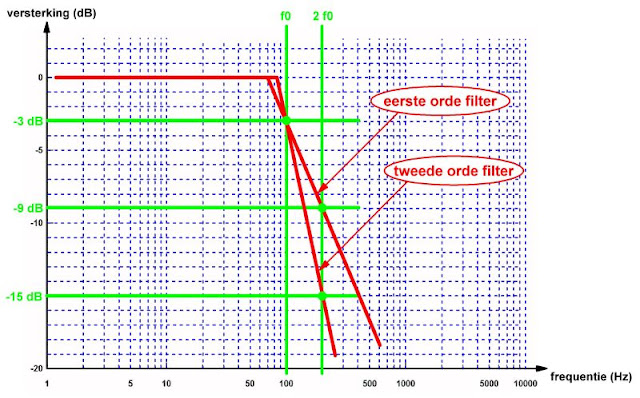 |
| Het begrip 'orde van een filter' grafisch toegelicht. (© 2019 Jos Verstraten) |
Als u aan een filter een zuiver sinusoídaal verlopende spanning legt en u zet met een tweekanaals oscilloscoop de in- en de uitgangsspanning van het filter op het scherm, dan stelt u iets uiterst merkwaardig vast. Zoals uit de onderstaande figuur blijkt ontstaat er een faseverschil tussen beide spanningen. Het is net alsof het filter het signaal iets vertraagt. Dit faseverschil φ wordt uitgedrukt in graden (°). De volle periode van de sinus wordt ingedeeld in 360°. U kunt dan meten met hoeveel graden de faseverschuiving φ overeenkomt. Het faseverschil is niet constant, maar afhankelijk van de frequentie. In het onderstaande oscillogram is dit faseverschil weergegeven met de twee rode verticale lijnen.
 |
| Tussen de in- en de uitgangsspanning van een filter ontstaat een faseverschil. (© 2019 Jos Verstraten) |
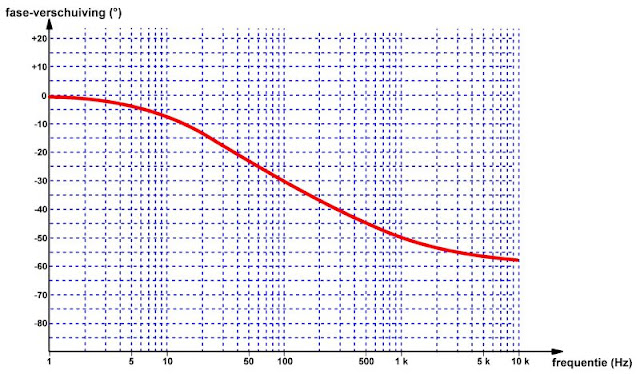 |
| De fase-karakteristiek van een filter. (© 2019 Jos Verstraten) |
Vaak worden de amplitude- en de fase-karakteristieken van een filter in één grafiek weergegeven. Men spreekt dan van de 'Bode-plot' van het filter. De grafiek geeft immers zowel het eerste als het tweede Bode-diagram weer. In de onderstaande figuur is als voorbeeld de Bode-plot van een hoogdoorlaat filter getekend. Dergelijke plot's worden tegenwoordig niet meer zélf berekend, maar door simulatie-programma's op de computer, zoals in dit geval 'Matlab'. De bovenste verticale as geeft steeds de amplitude-karakteristiek in dB weer, de onderste verticale as de fase-karakteristiek in graden. De horizontale as geeft uiteraard de logaritmische frequentieverdeling weer.
 |
| De Bode-plot van een filter, berekend door MatLab. (© Ultimatemath) |
Uit het feit dat een filter faseverschuivingen introduceert kunt u afleiden dat een filter het ingangssignaal vertraagt. Een derde grafiek van ieder filter is dan ook de looptijd-karakteristiek. In deze grafiek wordt, alweer op een logaritmische frequentie-as, uitgezet hoeveel μs of ms signalen met een bepaalde frequentie vertraagd worden. Of, met andere woorden, hoe lang het signaal er over doet om van de ingang naar de uitgang van het filter te migreren.
De stap-respons van een filter
Als u aan de ingang van een filter opeens een spanningssprong legt, dan zal het filter daar op een heel specifieke manier op reageren. Het zal duidelijk zijn dat dezelfde plotselinge spanningssprong niet op de uitgang is terug te vinden. Een spanningssprong is immers, denk aan de theorie van Fourier, samengesteld uit een heleboel harmonische frequenties. Nu zal het filter voor al die frequenties verschillende faseverschuivingen en looptijden hebben.
Het gevolg is dat de samenstelling van het signaal door het filter grondig wordt beïnvloed. Een heel sprekend voorbeeld van dit gedrag is voorgesteld in de onderstaande figuur. Aan de ingang van een filter wordt een signaal gelegd (rode curve). Volgens Fourier kunt u dit signaal ontleden in twee sinusvormige spanningen, de eerste en de tweede harmonischen (groene curven). Het filter vertraagt de ene harmonische over een hoek van φ1 graden en de tweede harmonische over een hoek van φ2 graden. Op de uitgang verschijnt weer het samengestelde signaal (rode curve), maar vanwege de faseverschuivingen ziet dat signaal er heel anders uit dan het signaal aan de ingang. Natuurlijk hebben wij in dit voorbeeld het effect nogal overdreven weergegeven, maar in de praktijk moet u tóch rekening houden met dit verschijnsel.
 |
| De signaalvervorming die door de fase-karakteristíeken van een filter ontstaat. (© 2019 Jos Verstraten) |
Dergelijke eigenschappen van filters kunt u samenvatten in een grafiek, die men de stap-respons karakteristiek noemt. In de onderstaande figuur is een voorbeeld van de stap-respons van een filter getekend. De grafiek geeft het spanningsverloop weer (verticale as) in functie van de tijd (horizontale as).
Als standaard wordt aan de ingang een spanning met een amplitude van 1 V gelegd. De grafiek geeft het verband tussen deze sprong aan de ingang en de door het filter gegenereerde uitgangsspanning. De stap-respons geeft belangrijke informatie over hoe een filterschakeling zich in de praktijk zal gedragen. In het laboratorium wordt meestal gemeten met zuivere sinusoidale spanningen. In de praktijk zal een filter echter veel meer aan stapspanningen worden blootgesteld. Denk maar aan een filter in een audio-systeem waarvan het ingangssignaal alles behalve sinusoidaal is maar eerder de ene na de andere stapspanning voorstelt. Uit de stap-respons kunt u bijvoorbeeld afleiden of een filter een bepaald 'inslingerings-gedrag' vertoont en of er sprake is van 'overshoot' op het uitgangssignaal.
 |
| De stap-respons van een filter. (© 2019 Jos Verstraten) |
Een ideaal filter (als voorbeeld wordt een laagdoorlaat filter genomen) zou karakteristieken moeten vertonen zoals in de onderstaande figuur zijn samengevat. De amplitude-karakteristiek Uuit = f(Uin) verloopt kaarsrecht tot aan de filterfrequentie en vertoont nadien een oneindig hoge verzwakking. De fase-karakteristiek φ verloopt weliswaar met een helling, maar deze is kaarsrecht. De looptijdvertraging τ is voor alle frequenties constant.
Het zal duidelijk zijn dat een dergelijk ideaal filter in de praktijk niet bestaat. Maar het is de taak van filterontwerpers om deze ideale karakteristieken zo goed mogelijk te benaderen. En aan deze 'zo goed mogelijke benadering' zijn heel wat beroemde namen gekoppeld.
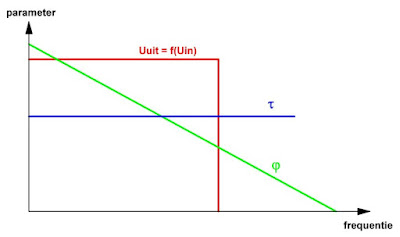 |
| De karakteristieken van een ideaal laagdoorlaat filter. (© 2019 Jos Verstraten) |
Filters worden rond transistoren of operationele versterkers opgebouwd. De schakelingen bestaan in alle gevallen uit netwerken van weerstanden en condensatoren die tussen de ingang van de schakeling en de ingangen en uitgang van de transistor of operationele versterkers zijn geschakeld. Het is van belang dat een dergelijke schakeling wordt aangestuurd uit een spanningsbron die een zo gering mogelijk inwendige weerstand bezit. Zou namelijk de waarde van de inwendige weerstand van de signaalbron te groot zijn, dan zal deze weerstandswaarde zich optellen bij de ingangsweerstand van de filterschakeling, waardoor de goede werking van het filter verstoord wordt.
Wat dit in de praktijk tot gevolg heeft is getekend in de onderstaande figuur. Het filter bestaat uit de onderdelen R1, C1 en de schakeling rond de operationele versterker. Uit dit schema blijkt overduidelijk wat er wordt bedoeld. Stel dat u kunt berekenen dat de weerstand R1 een waarde van 10 kΩ moet hebben om een bepaalde filter-karakteristiek te realiseren. Als de ingangsschakeling die het filter van signaal voorziet een eigen inwendige weerstand Ri heeft van 1 kΩ dan zal deze waarde in serie staan met R1. De reële waarde van de filterweerstand wordt dan 11 kΩ, hetgeen de karakteristieken van het filter kan verstoren.
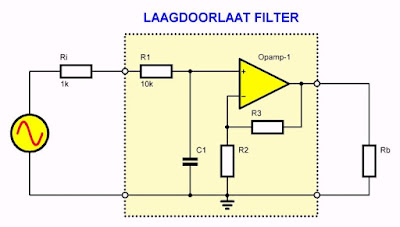 |
| De inwendige weerstand van de signaalbron telt zich op bij de ingangsweerstand van het filter. (© 2019 Jos Verstraten) |
Vandaar dat u tussen de ingang van de schakeling en de ingang van het echte filternetwerk steeds een buffertrap moet opnemen. Dat kan een als spanningsvolger geschakelde operationele versterker zijn, die een zeer hoge ingangsimpedantie heeft en een te verwaarlozen uitgangsimpedantie. Dit standaard systeem voor het aansturen van filters is getekend in de onderstaande figuur. Op deze manier wordt de werking van het filter volledig onafhankelijk van de eigenschappen van de signaalbron.
 |
| Het voorschakelen van een buffertrap. (© 2019 Jos Verstraten) |
Indeling volgens de karakteristieken
Inleiding
In het algemeen bestaat een filterschakeling uit een of meerdere operationele versterkers en een aantal weerstanden en condensatoren. De waarde van de weerstanden en de condensatoren bepaalt alle filter-karakteristieken. Het gevolg is dat een en dezelfde schakeling, met een bepaalde cutoff frequentie en een bepaalde steilheid, toch heel andere karakteristieken kan krijgen door andere waarden toe te kennen aan de weerstanden en de condensatoren.
Zo kunt u in filters van een hogere orde de karakteristieken in niet geringe mate beïnvloeden door de achter elkaar geschakelde filtertrappen iets afwijkende afsnijfrequenties f0 te geven. Het op deze manier benaderen van de ideale filter-karakteristieken is een bezigheid waar beroemde ontwerpers en wiskundigen zich mee bezig hebben gehouden. Er zijn tal van filter concepten ontwikkeld. Het ene concept optimaliseert de doorlaat-karakteristiek, maar legt minder nadruk op de fase-karakteristiek. Het andere concept probeert de looptijd zo ideaal mogelijk te maken, maar heeft als nadeel dat de doorlaat-karakteristiek niet zo vlak verloopt. In het algemeen kunt u stellen dat als u probeert één van de karakteristieken te verbeteren u onmiddellijk geconfronteerd wordt met een verslechtering van de overige karakteristieken. Een ideaal filter bestaat niet en aan welke eigenschap u het meeste belang hecht hangt af van de toepassing van het filter. Toch zijn er vier concepten die zich als standaard hebben doorgezet:
- Het Bessel filter.
- Het Butterworth filter.
- Het Chebyshev filter.
- Het Linkwitz/Riley filter.
In de volgende paragraafjes worden de specifieke eigenschappen van deze concepten in het kort beschreven.

Laagdoorlaat filters als voorbeeld
U kunt de vier filters ontwerpen als laagdoorlaat of als hoogdoorlaat filter. In de volgende paragrafen behandelen wij de eigenschappen van de concepten, geschakeld als laagdoorlaat filter. Dit soort filter zult u in de praktijk namelijk het vaakst aantreffen of moeten toepassen.
Het Bessel filter
De karakteristieken van dit filter concept werden weliswaar berekend door de wiskundige Bessel, maar uitvoerig in de praktijk getoetst door W. E. Thomson van het research laboratorium van de Britse Post. Vandaar dat men dit filter concept soms ook wel Thomson noemt of Bessel/Thomson.
Het Bessel filter heeft als voornaamste eigenschap een zo goed als ideale stap-respons. Deze is weergegeven in de onderstaande foto. Als u aan de ingang van een Bessel filter een blokspanning legt met een basisfrequentie die ver onder het verzwakkende frequentiegebied van het filter ligt, dan zal deze puls zo goed als onvervormd op de uitgang verschijnen.
 |
| De stap-respons van een Bessel filter. (© 2019 Jos Verstraten) |
 |
| De doorlaat-karakteristiek van een laagdoorlaat Bessel filter. (© 2019 Jos Verstraten) |
Het Butterworth filter
Het Butterworth filter heeft als voornaamste eigenschap dat de doorlaat-karakteristiek voor of na de afsnijfrequentie f0 zeer vlak verloopt. Dit wordt verduidelijkt aan de hand van de grafiek in de onderstaande figuur.
 |
| De doorlaat-karakteristiek van een laagdoorlaat Butterworth filter. (© 2019 Jos Verstraten) |
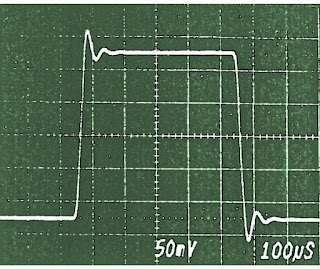 |
| De stap-respons van een Butterworth filter vertoont een duidelijke 'overshoot'. (© 2019 Jos Verstraten) |
Het Chebyshev filter
Als het er op aan komt zo scherp mogelijk te filteren na de afsnijfrequentie f0 en de overige karakteristieken van het filter er niet zo erg veel toe doen, dan is het Chebyshev concept de aangewezen filtervorm. Dergelijke scherp afsnijdende filters hebt u bijvoorbeeld nodig bij het samenstellen van anti-alias filters in analoog-naar-digitaal systemen. Uit de doorlaat-karakteristiek die in de onderstaande figuur is getekend blijkt overduidelijk dat het Chebyshev filter inderdaad het scherpst afsnijdt van alle drie. Maar ook duidelijk is dat in het door te laten frequentiegebied van een mooie rechte grafiek geen sprake is! De doorlaatband vertoont pieken en dalen die vaak dB's groot kunnen zijn.
 |
| De doorlaat-karakteristiek van een Chebyshev filter. (© 2019 Jos Verstraten) |
 |
| De stap-response van een Chebyshev filter. (© 2019 Jos Verstraten) |
Het Linkwitz/Riley filter
Speciaal ontwikkeld voor luidspreker scheidingsfilters
Linkwitz/Riley filters zijn in feite gewone laag- en hoogdoorlaat filters, waarvan de eigenschappen echter zijn geoptimaliseerd voor toepassing in scheidingsfilters van luidsprekers. Zoals u weet kunt u het gehele audiogebied van 20 Hz tot 20 kHz niet goed met één luidspreker weergeven.
Lage frequenties vereisen luidsprekers met grote magneetsystemen en grote stijve conussen die behoorlijk kunnen pompen. Hoge frequenties vereisen luidsprekertjes met kleine conussen die bovendien een heel ander stralingspatroon moeten hebben.
Vandaar dat in de meeste luidsprekersystemen minstens twee luidsprekers worden ingebouwd. Een grote woofer voor het weergegeven van de lage frequenties en een of twee tweeters voor het weergegeven van de hoge tonen.
Het komt er op aan het totale audiobereik op te splitsen in twee deelbereiken die ieder een luidspreker van signaal voorzien. Een typische klus waarvoor u filters moet inschakelen. Vroeger werden deze filters in de luidspreker behuizing zélf ingebouwd en bestonden deze uit condensatoren en spoelen. Deze LC-filters maken gebruik van de eigenschap dat de impedantie van een condensator kleiner wordt bij stijgende frequentie en de impedantie van een spoel groter wordt bij stijgende frequentie.
Ondanks de eenvoud hebben deze filters toch een steilheid van 12 dB/octaaf. In principe is deze steilheid groot genoeg voor deze toepassing, maar er is een probleem. Het zal duidelijk zijn dat u de afsnijfrequenties van beide filters heel precies op elkaar moet afstemmen. Met simpele LC-filters is dat vrijwel onmogelijk en ontstaat er een 'kuil' of een 'bult' in de weergavekarakteristiek rond de scheidingsfrequentie. Deze niet-lineariteit in de som van de amplitude-karakteristieken kan dB's groot zijn en dat is bij goede luidspreker systemen volstrekt ontoelaatbaar. Bovendien is het tweede probleem dat u noch de waarde van spoelen, noch de waarde van grote condensatoren zo precies gelijk kan maken aan de waarden die de meest rechte frequentie-karakteristiek opleveren.
De genoemde problemen zijn natuurlijk gemakkelijk op te lossen. U kunt immers actief gaan filteren. Na de voorversterker komen twee filters, een laagdoorlaat en een hoogdoorlaat en deze twee filters sturen ieder een eigen eindversterker. De ene eindversterker voedt de woofer-luidspreker, de tweede eindversterker de tweeter-luidspreker(s). Het probleem is nu herleid tot het ontwerpen van tweede of derde orde filters en u hebt heel wat meer ontwerpvrijheden bij RC-filters dan bij LC-filters.

Kritische karakteristieken
De vraag doet zich voor welk eigenschappen de twee filters moeten hebben voor dergelijke toepassingen. Om die eisen duidelijk op een rijtje te krijgen zou hier een behoorlijk stuk akoestische theorie opgevoerd moeten worden. Dat gaat een beetje te ver en vandaar dat de eisen alleen worden opgesomd, zonder nadere toelichting. Die eisen zijn nogal kritisch:
- Bij het kantelpunt (de crossover frequentie) moet het faseverschil tussen beide filters nul zijn, dit om te verhinderen dat de uitstralings-karakteristieken van de twee luidsprekers elkaar gaan beïnvloeden waardoor een soort 'gat' in het geluidsbeeld ontstaat.
- Bij het kantelpunt moeten beide filters precies 6 dB verzwakken om een piek of een dip in de som van de amplitude-karakteristieken te voorkomen.
- De door de filters geïntroduceerde faseverschillen in het ingangssignaal moet voor alle frequenties gelijk blijven, zodat de luidsprekers identieke uitstralings-karakteristieken behouden.
Het Linkwitz/Riley concept
Dit ideale actieve scheidingsfilter werd in 1976 grondig wiskundig onderzocht door Siegfried Linkwitz en Russ Riley. Zij vonden een nieuwe berekeningsmanier uit, waarbij zowel het laagdoorlaat als het hoogdoorlaat filter bij het kantelpunt een verzwakking van 6 dB konden vertonen, terwijl aan de twee andere voorwaarden ook werd voldaan. Het gevolg is dat de karakteristieken van een scheidingsfilter volgens het Linkwitz/Riley concept, getekend in de onderstaande figuur, het ideaal bijna perfect benaderen.
 |
| De weergave-karakteristiek van een Linkwitz/Riley filter. (© 2019 Jos Verstraten) |
In de meeste actieve luidspreker systemen worden tweede orde Linkwitz/Riley crossover filters toegepast. Deze hebben een helling van 12 dB/octaaf of 40 dB/decade. In de literatuur zult u deze filters vaak tegenkomen onder de notatie 'LR2' of 'LR-2'.
Koop uw digitale microscoop bij Amazon
