
|
Laagdoorlaat filters zijn zeer handige schakelingen omdat ze nuttig zijn bij het bestrijden van een van de grootste kwalen in de elektronica: ruis.
|
Het basisprincipe van een laagdoorlaat filter
Het onderdrukken van ruis
Zowel in de analoge als in de digitale elektronica is ruis een van de belangrijkste stoorsignalen waar u als elektronicus mee te maken krijgt. In de onderstaande figuur is bijvoorbeeld getekend wat er gebeurt als u een analoge spanning digitaliseert, opslaat in een geheugen en nadien weer omzet in een analoge spanning. De DAC die deze herwonnen analoge spanning maakt levert, per definitie, een 'trapvormige benadering' van de originele analoge spanning. Deze kleine sprongetjes in het signaal uiten zich onder de vorm van een hinderlijke 'digitale ruis' ook wel 'kwantiseringsruis' genoemd. Deze ruis kunt u uit het herwonnen analoge signaal verwijderen door gebruik te maken van een laagdoorlaat filter.
Ook bij het weergeven van oude LP's kunt u veel plezier beleven aan een laagdoorlaat filter dat de ruis die soms op oude opnames aanwezig is in min of meerdere mate elimineert.
 |
| Het verschijnsel 'digitale ruis' verklaard. (© 2019 Jos Verstraten) |
Alle analoge laagdoorlaat filters werken volgens een en hetzelfde principe. Deze filters bestaan uit een combinatie van weerstanden en condensatoren. Condensatoren hebben een impedantie (wisselspanningsweerstand) die afhankelijk is van de signaalfrequentie. Voor een frequentie van 0 Hz, dus voor gelijkspanning, hebben condensatoren een oneindig hoge impedantie. Voor een oneindig hoge frequentie hebben deze onderdelen een impedantie van 0 Ω. Dank zij deze eigenschap kunt u aan een filter de gewenste frequentie-afhankelijke eigenschappen geven.
Algemene achtergrondinformatie noodzakelijk
Zeggen termen als amplitude-karakteristiek, afsnijfrequentie, dB/octaaf, tweede orde filter, Bode-plot en Butterworth filter u niets? Dan raden wij u ten stelligste aan eerst het artikel Know-how: analoge filterschakelingen te lezen. In dat artikel maakt u kennis met algemene begrippen uit de analoge filtertechniek die ook in dit artikel aan de orde zullen komen.
Eerste orde laagdoorlaat filters
Eerste orde filter zonder versterking
Het basisschema van een laagdoorlaat filter van de eerste orde zonder versterking is getekend in de onderstaande figuur. De schakeling bestaat uit een passief RC-netwerk R1-C1, afgesloten met een als spanningsvolger geschakelde operationele versterker. De spanningsversterking in de doorlaatband van het filter bedraagt 1.
Nadien zal het filter met 6 dB/octaaf verzwakken. De amplitude-karakteristiek ziet er dus uit zoals rechts in de figuur is voorgesteld. Bij de afsnijfrequentie f0 bedraagt de verzwakking 3 dB.
 |
| Een eerste orde laagdoorlaat filter zonder versterking. (© 2019 Jos Verstraten) |
De werking van de schakeling is gemakkelijk te verklaren. Bij lage frequenties heeft de condensator een zeer hoge impedantie en kan verwaarloosd worden. De schakeling werkt dan als bufferversterker. Naarmate de frequentie stijgt zal de impedantie van de condensator een rol gaan spelen. Er ontstaat een spanningsdeler, gevormd door de vaste impedantie van de weerstand en de variabele impedantie van de condensator. Naarmate de frequentie stijgt zal een steeds groter deel van de ingangsspanning over de weerstand vallen en een steeds kleiner deel over de condensator. De schakeling gaat dus frequentie-selectief verzwakken.
Het zal duidelijk zijn dat een dergelijk filter geen goede eigenschappen heeft en in de praktijk niet vaak gebruikt zal worden.
Eerste orde filter met versterking
Het basisschema van een eerste orde laagdoorlaat filter kunt u uitbreiden tot het schema dat in de onderstaande figuur wordt voorgesteld. De operationele versterker is nu geschakeld als niet-inverterende spanningsversterker. De versterkingsfactor wordt bepaald door de verhouding tussen de weerstanden R2 en R3.
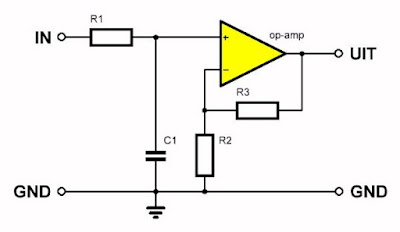 |
| Een eerste orde laagdoorlaat filter met spanningsversterking. (© 2019 Jos Verstraten) |
De afsnijfrequentie f0 van het eerste orde laagdoorlaat filter wordt gegeven door de formule:
f0 = 1 / [2 ● π ● R1 ● C1]
Hierin staat π voor 'pi', het beroemde getal met als waarde 3,1415.
Opmerking
Het zal duidelijk zijn dat er bij een eerste orde filter absoluut geen sprake is van diverse concepten, zoals Bessel, Butterworth of Chebyshev. De schakeling doet wat hij doet en daar blijft het bij!
Tweede orde laagdoorlaat filters
Opmerking
Deze filters gaan ook door het leven onder de naam Sallen & Key filters.
Tweede orde filter zonder versterking
Heel wat interessanter is het basisschema van een laagdoorlaat filter van de tweede orde, getekend in de onderstaande figuur. Er zijn nu twee RC-netwerken aanwezig, waarvan het tweede wordt opgenomen in de terugkoppeling van de operationele versterker. De werking is als volgt. Bij lage frequenties hebben de condensatoren zeer hoge impedanties en kunnen verwaarloosd worden. Het schema herleidt zich dan tot een bufferversterker, waarbij de twee weerstanden in serie met de ingang zijn opgenomen. Omdat echter de ingang van de operationele versterker een zeer hoge impedantie heeft, zal over deze weerstanden geen spanning vallen. De versterking van de schakeling is gelijk aan 1.
Naarmate de frequentie stijgt zal de impedantie van de condensatoren steeds kleiner worden. Er ontstaat een terugkoppeling van de uitgang naar de ingang via condensator C1. Condensator C2 vormt weer de spanningsdeler van het eerste orde filter. Het gevolg van deze dubbele werking is dat het filter na de afsnijfrequentie met 12 dB/octaaf gaat verzwakken.
 |
| Basisschema van een laagdoorlaat filter van de tweede orde zonder versterking. (© 2019 Jos Verstraten) |
In de meeste gevallen kunt u aan de twee weerstanden identieke waarden geven. De karakteristieken van het filter rond de afsnijfrequentie f0 zijn afhankelijk van de verhouding tussen de twee condensatoren. Deze eigenschap wordt uitgedrukt door de kwaliteitsfactor Q van het filter.
Voor de beschreven schakeling kunt u deze factor berekenen met de uitdrukking:
Q = √ [R1 ● R2 ● C1 ● C2] / [C2 ● (R1 + R2)]
Het is een beetje moeilijk om wiskundige formules in Internet-code te schrijven. Met √ wordt het vierkantswortel teken bedoeld dat in deze formule betrekking heeft op [R1 ● R2 ● C1 ● C2].
De invloed van de kwaliteitsfactor op de amplitude-karakteristiek is getekend in de onderstaande figuur. U ziet drie praktische curves getekend voor kwaliteitsfactoren tussen 1 en 0,5. Duidelijk blijkt dat alle drie de curves de 12 dB/octaaf helling volgen (hetgeen te verwachten was), maar dat rond de afsnijfrequentie sprake kan zijn van extra verzwakking of van lichte signaalopslingering. Als u prijs stelt op een zo vlak mogelijke amplitude-karakteristiek geeft u Q een waarde van precies 0,707!
 |
| De invloed van de kwaliteitsfactor Q op de amplitude-karakteristiek van het tweede orde filter. (© 2019 Jos Verstraten) |
Het zal duidelijk zijn dat u het filterschema zonder versterking weer op een heel eenvoudige manier kunt ombouwen tot een schakeling mét signaalversterking. Het schema is getekend in de onderstaande figuur. De spanningsversterking wordt ook nu bepaald door de verhouding van de weerstanden R3 en R4.
 |
| Een tweede orde filter met spanningsversterking. (© 2019 Jos Verstraten) |
Bij het tweede orde laagdoorlaat filter komen de heren Bessel, Chebyshev en Butterworth een woordje meepraten. Als u namelijk de twee weerstanden en de twee condensatoren van het filternetwerk identieke waarden R en C geeft, dan blijkt dat de verhouding tussen de weerstanden R3 en R4 heel veel invloed heeft op de karakteristieken van het filter. U kunt een terugkoppelfactor α definiëren waarvan de waarde wordt gegeven door de formule:
α = R3 / [R3 + R4]
Door deze verhouding α een foutieve waarde te geven kunt u de schakeling zelfs laten oscilleren! In de onderstaande tabel worden de waarde van deze weerstanden gegeven voor de drie filter-concepten. De waarde van de overige componenten is:
R1 = R2 = R = 15,9 kΩ
C1 = C2 = C = 10 nF
Voor Chebyshev gelden twee waarden, namelijk +1,25 dB en +3,0 dB. Dit zijn de waarden van de maximale opslingeringen in de amplitude-karakteristiek die u wilt tolereren.
 |
| De verhouding tussen de terugkoppelweerstanden bepaalt de karakteristieken van het filter. (© 2019 Jos Verstraten) |
In de onderstaande figuur is een manier getekend waarmee u door het simpelweg verdraaien van een potentiometer van het ene naar het andere filter-concept kunt omschakelen. Dat is uiteraard een vloeiend gebeuren en u kunt niet zeggen 'nu verlaat ik het Bessel-gebied en kom in de zone van Butterworth terecht' of iets dergelijks!
Als de potentiometer in de bovenste stand staat (α = 1) hebt u de versterking van de operationele versterker uitgeschakeld en staat deze geschakeld als spanningsbuffer. Naarmate u de loper van de potentiometer meer naar onder verplaatst daalt de waarde van α en ontstaan respectievelijk de Bessel, Butterworth en Chebyshev karakteristieken. Maar er is een grens! Als u namelijk de loper van de potentiometer te veel naar onder verplaatst dan gaat de schakeling steeds meer versterken en neemt de waarde van de kwaliteitsfactor Q steeds meer af. Bij α gelijk aan 0,333 gaat de schakeling niet meer als filter werken, maar als oscillator!
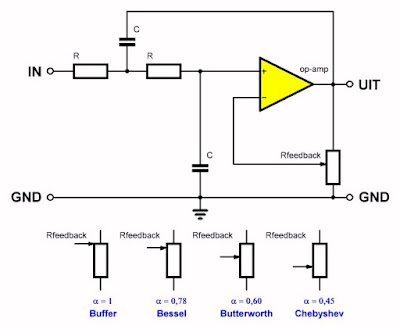 |
| Een praktische manier om de verschillende filter-concepten uit te proberen. (© 2019 Jos Verstraten) |
Het tot nu toe besproken schema geeft dé standaard schakeling voor een actief laagdoorlaat filter van de tweede orde. Op dit schema zijn echter ontelbare variaties gemaakt, waarvan er nu een in het kort wordt besproken. Dit zogenoemde MFB-filter, letterwoord voor 'Multiple FeedBack' heeft een meervoudige terugkoppeling, zie de onderstaande figuur.
Het zou in het kader van dit artikel te ver gaan om alle eigenschappen van dit filter te bespreken. Het voordeel van de extra terugkoppeling is echter dat de schakeling stabieler is en minder gemakkelijk in een toestand terecht komt waarvan sprake kan zijn van oscillatie.
 |
| Het basisschema van het MFB-filter. (© 2019 Jos Verstraten) |
Een toepassing van een tweede orde laagdoorlaat filter
Ruisfilter voor vinyl platen
Op dit moment beleeft de aloude vinyl plaat een herleving. Dat brengt u misschien op de idee op een eventueel op zolder aanwezige hoeveelheid oeroude LP's weer eens te beluisteren. Nostalgie! Hoewel natuurlijk niet volstrekt noodzakelijk, is een goed ruisfilter dan een nuttige aanvulling op uw analoog geluidsweergave systeem. Met zo'n filter kunt u het ruisen en spetteren van oude of vaak gedraaide platen aanmerkelijk reduceren.
Het onderstaande schema geeft het praktisch bruikbare schema van een tweede orde laagdoorlaat filter met drie kantelfrequenties van 5, 7 en 11 kHz. De steilheid van de onderdrukking van de hoge frequenties is 12 dB/octaaf, zodat het nuttige geluidssignaal zo veel mogelijk gespaard wordt. Door middel van een extra schakelaar S2 kunt u het filter uitschakelen, waarbij de in- en uitgang rechtstreeks worden doorverbonden. De versterking van de niet verzwakte signalen is gelijk aan een, zodat het inbouwen van het filter in uw geluidsweergave systeem geen nare gevolgen heeft voor de instelling van de volumeregelaar.
Omdat de meeste draaitafels zijn uitgerust met een elektrodynamisch element moet u echter ook een RIAA-versterker toepassen. De uitgang van deze versterker kunt u aansluiten op de ingang van dit ruisfilter. De uitgang van het filter voert u naar een van de AUX-ingangen van uw versterker.
In tegenstelling tot alle tot nu toe gepubliceerde schakelingen in dit artikel wordt in deze schakeling geen gebruik gemaakt van een operationele versterker, maar van twee oude transistoren van het type BC109C. Deze staan bekend om hun uitstekende ruiseigenschappen en vandaar dat zij in deze schakeling worden toegepast.
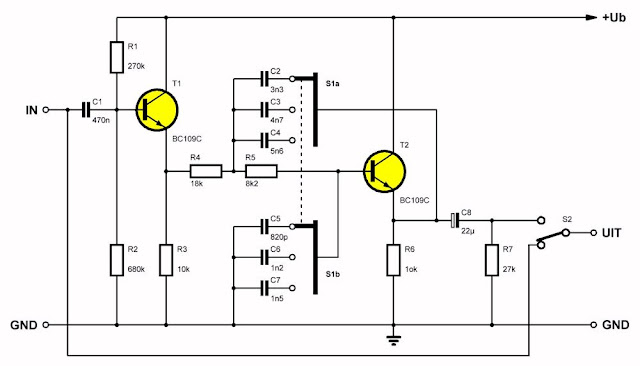 |
| Een tweede orde filter als ruisonderdrukker voor LP's. (© 2019 Jos Verstraten) |

De ingangsspanning wordt aangeboden aan de basis van de eerste transistor via de scheidingscondensator C1. Deze condensator scheidt signaalspanning en instelspanning.
Het filter heeft drie instelbare kantelpunten. Deze kantelpunten worden verkregen door de waarde van de condensatoren in het actieve filter te veranderen. Dit gebeurt door middel van de schakelaars Sla en S1b. De uitgangsspanning van het filter wordt door middel van een RC-filter C8-R7 afgenomen van de emitter van de tweede transistor.
Uiteraard is het tweede kanaal volledig identiek van opbouw. De voeding +Ub voor beide filters kunt u aftakken van een goed afgevlakte voeding van minimaal 12 V.
Hogere orde filters
Cascaderen van besproken schakelingen
Laagdoorlaat filters van de derde, vierde, vijfde, etc. orde ontstaan door eerste en tweede orde filters achter elkaar te schakelen. Dat noemt men 'cascaderen' van de schakelingen.
Een derde orde filter
Zo is in de onderstaande figuur een derde orde filter getekend, samengesteld uit de reeds bekende schakelingen van het eerste en tweede orde filter. Merk op dat de als buffer geschakelde operationele versterker die bij het eerste orde filter hoort, niet in het schema is opgenomen. Het gevolg is dat het eerste orde filter enige invloed heeft op het tweede orde filter. De weerstanden zijn immers in serie geschakeld.
 |
| Een laagdoorlaat filter van de derde orde. (© 2019 Jos Verstraten) |
Op een identieke manier kunt u, zie de onderstaande figuur, een vijfde orde filter ontwerpen door twee filters van respectievelijk de tweede en de derde orde achter elkaar te schakelen. Een dergelijk filter heeft een steilheid van 30 dB/octaaf en dat is heel wat!
 |
| Een laagdoorlaat filter van de vijfde orde. (© 2019 Jos Verstraten) |
Berekenen van laagdoorlaat filters met FilterLab
FilterLab 2.0
De tijd dat u ingewikkelde formules moest gebruiken voor het berekenen van analoge filters ligt gelukkig achter ons. Er bestaat mooie freeware software die dat klusje voor u doet. Een van de mooiste programma's , maar dat is uiteraard een zeer persoonlijke smaak, is 'FilterLab' dat gratis ter beschikking wordt gesteld door de IC-fabrikant Microchip. Van dit Windows-programma is bij het publiceren van dit artikel versie 2.0 beschikbaar. Het programma én een zeer uitgebreide Engelstalige handleiding van niet minder dan 76 pagina's kunt u downloaden van:
https://www.microchip.com/developmenttools/ProductDetails/filterlabdesignsoftware
Voor het geval dat deze software, op het moment dat u dit artikel leest, niet meer beschikbaar zou zijn via Internet kunt u altijd een kopie opvragen bij de auteur van dit blog via josverstraten@live.nl.
De mogelijkheden met FilterLab 2.0
Met deze freeware kunt u laagdoorlaat filters berekenen tot de achtste orde en wel volgens de filter-concepten van Chebychev, Bessel en Butterworth. Het frequentiebereik gaat van 0,1 Hz to 1 MHz.

Het installeren van FilterLab 2.0
Wij hebben deze software geïnstalleerd op een Windows 7.0 systeem en dat gaat volledig automatisch en zonder enig probleem. Maak wél eerst een nieuwe map aan voor deze software, zodat u het programma gemakkelijk kunt terugvinden. Er wordt namelijk geen snelkoppeling op uw bureaublad geïnstalleerd.
De Filter Specification
Via het menu 'Filter' en de optie 'Design' komt u in het onderstaande venster terecht waar u als eerste in het tabblad 'Filter Specification' voor 'Lowpass' en het door u begeerde filter-concept kiest. Met 'Overall Filter Gain' kunt u de gewenste versterking van de schakeling instellen, niet in dB maar gewoon als factor.
 |
| Het selecteren van het soort filter in FilterLab 2.0. (© 2019 Jos Verstraten) |
In dit tabblad vult u de orde van het filter in (Force Filter Order), de gewenste verzwakking in dB bij de afsnijfrequentie f0 (Passband Attenuation) in dB en de gewenste afsnijfrequentie (Passband Frequency).
 |
| Het selecteren van de parameters van het filter. (© 2019 Jos Verstraten) |
In het tabblad 'Circuit' kunt u de gewenste schakeling kiezen. Het Sallen & Key schema ligt hier voor de hand, maar u kunt ook voor het MFB-schema kiezen. Selecteer vervolgens de keuze 'Standard 1 %', zodat het programma standaard weerstand- en condensatorwaarden berekent. U hebt de mogelijkheid om de waarde van de condensatoren vast te leggen, bijvoorbeeld omdat u al nauwkeurige waarden in huis hebt en u het programma alleen de weerstanden die bij deze condensatoren passen wilt laten berekenen.
 |
| Het selecteren van het soort schakeling en de waarde van de condensatoren. (© 2019 Jos Verstraten) |
Na een klik op 'OK' verschijnt onmiddellijk de door FilterLab berekende schakeling in een eigen venstertje op uw scherm. In gelijksoortige venstertjes kunt u ook de frequentie- en de fase-karakteristieken van het filter weergeven. Uiteraard kunt u zowel het schema als de karakteristieken printen met de systeem-printer van Windows.
 |
| Het door FilterLab berekende schema van het filter. (© 2019 Jos Verstraten) |
Soldeerbout met temperatuurindicatie
