Know-how: MP3 audio-compressie

(gepubliceerd op 10-09-2023)

Met het door het 'Fraunhofer Institut' ontwikkelde MP3-algoritme kunt u een nummer dat op een audio-CD 27,5 MB in beslag neemt omzetten in een bestand van slechts 2,5 MB met vrijwel dezelfde kwaliteit. Maar daar is heel wat voor nodig!

Inleidende begrippen

Lineaire sampling met 2 x 16 bits

Toen men begon met het ontwikkelen van de audio-CD vroeg men zich af met hoeveel bits geluid gesampled moest worden om een met analoge audio vergelijkbare kwaliteit te verkrijgen. Na uitgebreide experimenten met orkesten, vinylplaten en digitale audio, onder andere door Philips uitgevoerd in het Concertgebouw in Amsterdam, kwam men tot de conclusie dat analoog stereo-geluid dat met 2 x 16 bits werd gesampled na herwinning een voor de meeste luisteraars aanvaardbare kwaliteit opleverde.

Die 2 x 16 bits werd dé standaard voor het digitaliseren van audio voor niet-professioneel gebruik. Niet alleen de audio-CD maakte gebruik van deze technologie, maar ook het standaard door Windows ondersteunde bestandsformaat voor digitale audio, WAV, werkte volgens dit systeem.

44.100 samples per seconde

Een tweede vraag was uiteraard hoeveel van die 2 x 16 bits brede samples er per seconde moesten worden genomen om de goede kwaliteit van 2 x 16 bits te handhaven. Ook hiermee werd uitgebreid geëxperimenteerd en als compromis werd een aantal van 44.100 samples per seconde gestandaardiseerd.

Lineaire sampling

Als derde onderdeel van de standaard werd afgesproken dat er geen enkele vorm van data-reductie op de datastroom zou worden toegepast. Dat wil zeggen dat altijd de momentele waarden van de twee analoge geluidssignalen van het linker en rechter kanaal 44.100 keer per seconde worden omgezet in 2 x 16 bits brede digitale codes. Zelfs als er in de muziek een zeer stille passage voorkomt en die stilte best wel met vier bits gedigitaliseerd zou kunnen worden, moeten er tóch 44.000 samples van 2 x 16 bits worden genomen.

Dat noemt men 'lineaire sampling' en dit systeem heeft als voordeel dat het technisch eenvoudig is te realiseren. Het grote nadeel is echter dat één seconde geluid onder alle omstandigheden wordt omgezet in een datastroom van niet minder dan 1.411.200 bits oftewel 1,4 Mb!

Voor heel veel toepassingen veel te veel

Die 1,4 Mb/s kon nog nét geschreven worden op en gelezen van een audio-CD. Maar naarmate er meer behoefte ontstond aan het via datacommunicatie verzenden van audio werd deze forse datastroom een grote beperking. Er ontstond behoefte aan een systeem dat audio met een veel kleinere datastroom kon digitaliseren, zonder echter veel concessies te doen aan de kwaliteit van het geluid.

MP3 van het  'Fraunhofer Institut'

De oplossing voor dit probleem, MP3, werd in 1991 ontwikkeld door het Duitse 'Fraunhofer Institut', in samenwerking met de Universiteit van Erlangen. MP3 is in staat de omvang van WAV-files met een factor 10 tot 12 te reduceren, zonder merkbaar kwaliteitsverlies. Door WAV-bestanden om te zetten in MP3, daalt de bitrate dus tot gemiddeld 117,7 kb/s. Neemt u genoegen met mindere kwaliteit of wilt u alleen gesproken tekst in telefoon-kwaliteit verzenden, dan kan MP3 de gegevensstroom van WAV zelfs met een factor 96 reduceren!

Het nummer 'Tom's Diner' van Suzanne Vega was het eerste nummer dat werd gebruikt om de kwaliteit van het MP3-formaat te testen en het algoritme te verfijnen. Na iedere aanpassing luisterde men naar dit nummer, waarbij men ervoor zorgde dat de subtiliteit van Vega's stem niet nadelig werd beïnvloed. Dit nummer werd gekozen vanwege zijn bijna monofone karakter en brede spectrale inhoud, waardoor het gemakkelijker mogelijk werd om onvolkomenheden in het compressie-algoritme te horen tijdens het afspelen. 

Moving Picture Experts Group

De Moving Picture Experts Group (MPEG), de internationale organisatie die de standaarden voor digitale video vastlegt, nam MP3 op als onderdeel van zijn MPEG-1 en later MPEG-2 standaarden. In deze standaarden worden de MP3 audio-gegevens dan ook MPEG-1 Audio en MPEG-2 Audio genoemd.

MP3 wordt een internationale standaard

Op 7 juli 1994 bracht het 'Fraunhofer Institut' de eerste softwarematige MP3-encoder uit, genaamd 'l3enc'. Hierdoor kon vrijwel iedereen aan de slag met het omzetten van WAV-of audio-CD bestanden naar MP3.

De bestandsnaam extensie .MP3 werd op 14 juli 1995 door het 'Fraunhofer'-team gekozen, voorheen werden de bestanden .BIT genoemd. Op 9 september 1995 werd de eerste real-time softwarematige MP3-decoder 'WinPlay3' op de markt gezet. Hiermee werd het voor het grote publiek mogelijk om MP3-bestanden af te spelen op een gewone PC. 

MP3 brak helemaal door als dé standaard voor het verzenden en afspelen van digitale audio met de komst van Nullsoft's beroemde audiospeler 'Winamp', uitgebracht in 1997. Dit programma staat nu nog steeds op vrijwel iedere Windows-PC als versie 5.9.2.

In november van hetzelfde jaar verscheen de website 'mp3.com' op het internet, waarvan duizenden muzieknummers, omgezet naar MP3-formaat, gratis gedownload konden worden. Het succes van deze (en vele andere soortgelijke sites) was uiteraard te danken aan de kleine omvang van de MP3-bestanden, die snel waren te downloaden en tóch uitstekende kwaliteit muziek leverden. In dat jaar werd ook het begrip 'muziekpiraterij' gelanceerd door de muziekuitgeverijen, die hun omzet zagen kelderen en begonnen met rechtszaken aan te spannen tegen websites en individuele massa-downloaders van illegale MP3's.

In 1998 werd de eerste draagbare solid-state digitale audiospeler 'MPMan' van SaeHan Information Systems uitgebracht.

Verliesgevende (lossy) compressie

Het MP3-algoritme creëert per definitie bestanden die niet identiek zijn aan de originele digitale opname. Men noemt dit 'verliesgevende' of 'lossy' compressie. Er worden dus details van de audio-informatie opgeofferd om de datastroom kleiner te maken. Dit is wat door audiofielen wordt gezien als het grootste bezwaar tegen MP3. Zij beweren dat zelfs bij de hoogste bitrate-instellingen MP3-bestanden hoorbaar inferieur zijn aan audio-CD's en vinylplaten. Maar andere mensen die over een goed muzikaal getraind gehoor beschikken beweren dat dit onzin is en dat het voor het menselijk oor onmogelijk is om het verschil te detecteren tussen een ongecomprimeerd CD-bestand en een MP3-bestand gecodeerd met een bitsnelheid van 320 kb/s. Dat is uiteraard net zo'n zinloze maar eindeloze discussie als die ontstaat over de vraag of mensen in staat zijn een harmonische vervorming van 0,1 % te horen.

Bij het maken van een MP3-bestand kan men bovendien kiezen hoeveel informatie er verloren gaat tijdens het coderings- en compressie-proces. Het is zonder meer mogelijk om vanuit dezelfde gegevensbron, bijvoorbeeld een WAV-bestand, twee verschillende MP3-bestanden met zeer  verschillende geluidskwaliteit en bestandsgroottes te maken.

Combinatie van bekende technieken 

De compressie-technieken die worden toegepast bij MP3 zijn niet nieuw. In feite wordt gebruik gemaakt van de door Philips ontwikkelde techniek van PASC, toegepast bij het geflopte DCC-systeem en van zeer ingewikkelde wiskundige technieken, toegepast bij de video-codering van MPEG. De combinatie van beide technieken is echter uniek en levert spectaculaire resultaten op! 

De data-reductie volgens MP3 is gebaseerd op de onderstaande principes: 

       - De drempelwaarde van het menselijke gehoor.

       - Het invoeren van sub-banden.

       - Het maskeereffect van het menselijke gehoor.

       - Adaptive bit allocation.

       - Middeling van het gemiddelde niveau.

       - Discrete cosinus transformatie. 

       - Run length codering.

       - Entropie-codering.

       - Frequentie-begrenzing. 

MP3, stap na stap

De drempelwaarde van het menselijke gehoor 

Het menselijke gehoor is frequentieselectief gevoelig. Dat betekent dat er een gehoorcurve kan worden opgesteld zoals getekend in de onderstaande figuur. Men kan een 'threshold' opstellen, een lijn die aangeeft waar voor iedere frequentie de drempelwaarde van het gehoor ligt. Geluiden die zwakker zijn dan deze drempelwaarde worden niet waargenomen. Het is niet noodzakelijk dergelijke geluiden te coderen. In het getekende voorbeeld zal MP3 het geluid met een frequentie van 60 Hz weglaten en niet digitaliseren. U hoort het toch niet!

De gehoorcurve van het menselijke gehoor. (© 2023 Jos Verstraten)

Invoeren van sub-banden 

In de praktijk is het uiteraard onmogelijk om het threshold-proces voor iedere frequentie uit te voeren. Het frequentiebereik van het audiosignaal wordt in 32 sub-bandjes ingedeeld, die ieder vrij smal zijn. Deze bandjes zijn, zie de onderstaande figuur, lineair over de frequentie-as verdeeld. Nadien berekent het MP3-algoritme voor iedere sub-band de verhouding tussen het actuele signaalniveau en de vast geprogrammeerde threshold van deze band. Ligt de amplitude-inhoud van een sub-bandje onder de gehoordrempel, dan wordt de inhoud van dat bandje niet gecodeerd.

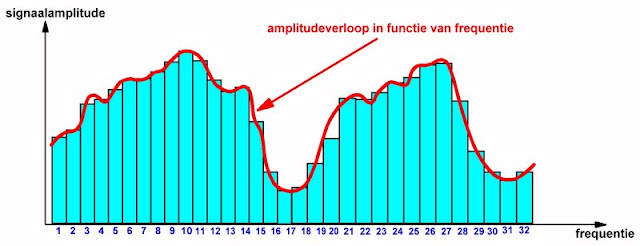MP3 werkt met 32 sub-bandjes met een zeer kleine bandbreedte.
(© 2023 Jos Verstraten)

Het maskeereffect van het menselijke gehoor 

Het menselijke gehoor vertoont een bepaald maskeereffect. Dit verschijnsel wordt toegelicht aan de hand van de onderstaande grafiek. Een sterk signaal A kan een in frequentie vlakbij gelegen zwakker signaal B maskeren, het gehoor zal dat tweede signaal niet waarnemen, ondanks dat de amplitude boven de gehoordrempel ligt. Een tweede maskeereffect ontstaat in de tijd. Als een zacht geluid een paar milliseconde eerder door een hard geluid is voorafgegaan, dan zal het zachte geluid niet waarneembaar zijn. Deze verschijnselen werden reeds in 1894 waargenomen door de Amerikaanse natuurkundige Alfred M. Mayer. In 1959 beschreef Richard Ehmer een complete reeks auditieve curven met betrekking tot dit fenomeen.

Het MP3-algoritme houdt rekening met deze twee maskeereffecten. De software voert een continue analyse uit van het amplitudeverloop in ieder van de sub-bandjes, vergelijkt de gegevens van een sub-band met de analyses van de aangrenzende sub-bandjes en analyseert bovendien het amplitudeverloop in functie van de tijd. Aan de hand van al deze gegevens besluit de software welke signalen wél en welke signalen niet verder worden verwerkt.

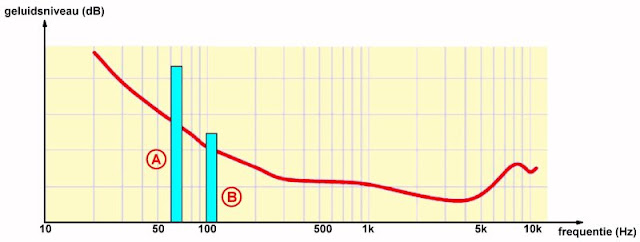Het maskeereffect van het menselijk gehoor. (© 2023 Jos Verstraten)

Adaptive bit allocation

De volgende stap is dat alles dat boven de gehoor- en maskeerdrempels ligt digitaal verwerkt moet worden. MP3 werkt met een zogenoemde 'floating point quantisering'. Dit is een dynamisch proces, waarbij MP3 alleen zoveel bits aan een monster toewijst als nodig voor het kwantiseren van het monster. Voor het ene monster kan dat noodzakelijke aantal bits bijvoorbeeld 19 bedragen, voor een volgend monster kan het echter best zijn dat 4 bits volstaat. De bits van ieder monster worden ingedeeld in twee groepen. Een aantal bepaalt een zogenoemde schaalfactor, de overige bits staan ter beschikking voor de kwantisering van het monster. Dit wordt toegelicht aan de hand van de onderstaande figuur. 

De twee groepen bits van ieder sample. (© 2023 Jos Verstraten)

Het ingewikkelde proces van het toewijzen van de bits aan ieder sample wordt toegelicht aan de hand van de onderstaande figuur. In deze figuur worden tien monsters beschouwd in tien verschillende sub-bandjes. De gestippeld getekende monsters worden niet gekwantiseerd, omdat zij onder de drempels van het gehoor liggen. Blijven dus over de monsters A, B, C en D. Het gedeelte van de amplitude dat onder de threshold-curve ligt kan in één keer worden gedefinieerd door een schaal constante in te voeren. Deze constante is natuurlijk voor iedere sub-band anders. De waarde van de schaalfactor wordt opgeslagen in de eerste bits. Nadien codeert MP3 alleen dat deel van de amplitude dat boven de gehoordrempel ligt. Bovendien kijkt het systeem naar de grootte van deze amplitudes. Signaal C zit bijvoorbeeld maar iets boven de gehoordrempel en wordt met slechts 2 bits gecodeerd. De amplitude van signaal A is echter groot en MP3 stelt daarvoor dan ook bijvoorbeeld tien bits ter beschikking.

Zo zal het dus maar zelden voorkomen dat MP3 de 16 standaard bits van audio-CD of WAV nodig heeft om één sample te kwantiseren, hetgeen een aanzienlijke data-reductie tot gevolg heeft.

De adaptieve bit-toekenning zorgt voor een zeer forse data-reductie.
(© 2023 Jos Verstraten)

Middeling van het gemiddelde niveau 

Een verdere data-reductie wordt bereikt door de digitale codes van diverse opeenvolgende monsters in een zogenoemd 'raam' samen te voegen. Onderzoeken hebben uitgewezen dat de amplitude van een geluidssignaal, vergeleken met de samplingfrequentie van 44,1 kHz, maar zeer langzaam varieert. Dat wil zeggen dat men van een reeks opeenvolgende samples een gemiddelde waarde kan berekenen en dat de individuele samples maar weinig van deze waarde zullen afwijken. Vandaar dat deze gemiddelde signaalwaarde over een periode van een aantal samples wordt berekend en dat deze eenmalig in een digitale schaalfactor wordt ondergebracht. Nadien volstaat het voor deze monsters alleen de afwijkingen van de gemiddelde waarde in de code op te nemen. Hiervoor volstaan in de meeste gevallen drie bits. 

Dit principe wordt in de onderstaande figuur toegelicht aan de hand van een voorbeeld. Het analoge signaal schommelt in dit voorbeeld rond een gemiddelde waarde van 2,0 mV. MP3 berekent deze waarde en stelt de schaal-factor voor deze monsters vast op 'L-H-L-H'. Nadien berekent de software de amplitude-afwijking van ieder monster ten opzichte van de gemiddelde waarde en codeert deze met drie bits. Voor het volledig definiëren van de twaalf monsters uit dit voorbeeld zou MP3 dus slechts 4 + [12 ● 3] = 40 bit nodig hebben, heel wat minder dan de 12 ● 16 = 192 bit van audio-CD of WAV. 

Aanzienlijke data-reductie door het invoeren van een gemiddelde waarde.
(© 2023 Jos Verstraten)

Discrete cosinus transformatie 

Een volgende zeer belangrijke stap in de reductie van de hoeveelheid data wordt bereikt door beroep te doen op 'DCT' oftewel 'Discrete Cosinus Transformatie'. DCT is een proces waarbij een zogenoemd 'tweedimensioneel continu amplitudeverloop' kan worden omgezet in een zogenoemd 'ruimtelijk discreet frequentiespectrum'. 

Dit algoritme, voorgesteld door Nasir Ahmed in 1972, werd ontwikkeld door Ahmed samen met T. Natarajan en K.R. Rao in 1973, zij publiceerden hun resultaten in 1974. 

DCT is een heel ingewikkeld wiskundig proces. Het valt enigszins te vergelijken met de Fourier-transformatie die kan worden toegepast op eendimensionele continu amplitudeverlopen. Door bijvoorbeeld een rechthoekvormige puls (heeft één dimensie in de tijd) te ontleden met Fourier in zijn harmonische samenstelling kan de golfvorm helemaal worden beschreven met een wiskundige formule. Die formule bevat een aantal veelvouden van de basisfrequentie met ieder een bepaalde amplitude. Als u alle harmonische bestanddelen boven de tiende verwaarloost zal het uit de formule teruggehaalde signaal nog steeds in grote lijnen op de originele rechthoekvormige puls lijken. Discrete cosinus transformatie werkt op dezelfde manier, maar dan niet op een eendimensionele golfvorm, maar op een die twee dimensies heeft. Een simpel voorbeeldje zal dit (hopelijk) verduidelijken.

Een aantal, bijvoorbeeld 64, bytes van de data-stroom wordt opgenomen in een matrix, zie de onderstaande figuur. Deze wordt matrix-1 genoemd. In ieder hokje van de matrix staat één byte en de getalletjes in de hokjes geven de waarde van de bytes in normale decimale getallen weer. U kunt zich nu, met enige verbeelding, deze 64 getallen voorstellen door staafjes van een staven-grafiek. Het door de bovenzijde van deze staven gevormd oppervlak vertoont een golving, omdat de bytes uiteraard niet allemaal dezelfde waarde hebben. Dit golvend oppervlak van de bovenzijde van de byte-staafjes is nu dat 'tweedimensioneel continu amplitudeverloop', enigszins te vergelijken met het golvend Limburg heuvellandschap.

De eerste stap van de 'discrete cosinus transformatie'. (© 2023 Jos Verstraten)

Een dergelijk ruimtelijk verloop kan, door middel van de wiskundige theorie die 'discrete cosinus transformatie' heet, worden omgezet in een coëfficiënten-matrix, zie de onderstaande figuur. Het eerste dat opvalt is dat de getallen in deze matrix veel kleiner zijn dan de getallen in de eerste matrix. De getallen stellen nu géén decimale inhouden van de bytes meer voor, maar wiskundige coëfficiënten die het verloop in de 'golving' van de amplitude van de bytes op een bepaalde manier beschrijven. Deze coëfficiënten worden ook nu de 'harmonischen' genoemd. Toch kunt u, door op matrix-2 een 'Inverse Discrete Cosinus Transformatie' (IDCT) toe te passen uit deze coëfficiënten weer alle bytes nauwkeurig herberekenen.

De tweede stap van de 'discrete cosinus transformatie'. (© 2023 Jos Verstraten)

Het grote voordeel van de 'DCT' is dat er een heleboel hogere harmonischen zijn die een erg kleine waarde hebben. In feite zit de belangrijkste informatie nu alleen in de linker bovenhoek van de matrix. Een heel groot verschil met de grote getallen over de gehele matrix-1. Als al die kleine waarden van de hogere harmonischen op nul worden gesteld, zal dat nauwelijks gevolgen hebben voor het verloop van het deeltje van het audio-signaal, dat in de matrix-1 werd opgenomen. De DCT bereidt het systeem dus voor op een grote compressieslag, die in de volgende fase tot stand komt.

De kwantisering van de DCT-matrix

Dit komt er op neer dat grote getallen worden omgezet in kleinere getallen door de grote getallen te delen door een bepaalde factor. Kleine getallen worden door deze deling tot nul gereduceerd. Als u dus de gegevens uit een matrix-2 kwantiseert, dan zullen er een heleboel nullen in de matrix ontstaan. Als bijvoorbeeld wordt gekwantiseerd wordt door alle DCT-waarden te delen door 8, dan blijven er na de deling nog maar zes waarden over die niet gelijk zijn aan nul, zie matrix-3. Alle overige DCT-waarden zijn namelijk kleiner dan acht en worden tot nul gereduceerd als zij door acht gedeeld worden. Het aantal nullen in de matrix neemt toe en daarmee de compressiefactor (lees verder), maar bij het herwinnen van de audio-gegevens zal de originele matrix dus veel minder nauwkeurig gereconstrueerd worden dan zonder deze deling het geval zou zijn.

De kwantisering van de DCT-matrix. (© 2023 Jos Verstraten)

Hier ontstaat de verliesgevende (lossy) compressie

Matrix-2 is middels 'IDCT' nog volledig om te zetten in matrix-1. Echter, zelfs als u alle waarden uit matrix-3 weer met acht vermenigvuldigt en nadien 'IDCT' toepast, zult u maar een benadering krijgen van de waarden in matrix-1. Het invoeren van de kwantisering op de DCT-matrix heeft dus tot gevolg dat het originele geluid niet meer exact herwonnen kan worden. Lossy compression betekent dat er tijdens de compressie enige informatie wordt weggegooid en dat het originele bestand niet perfect kan worden hersteld uit de gecomprimeerde data. Maar deze vervorming kan blijkbaar zo klein worden gemaakt dat het menselijk gehoor er volledig ongevoelig voor is!

Dit is dé basis van de grote mate van compressie van MP3, maar wél een compressie die verliesgevend of lossy is.

Het vormen van de seriële datastroom 

Na het kwantiseren van de DCT-matrixen worden de gegevens zigzaggend uit de matrixen uitgelezen, zodat een seriële datastroom ontstaat. Het gevolg van deze zigzaggende uitlezing is dat er in de code vaak een heleboel nullen achter elkaar staan. Als de gegevens zigzaggend uit matrix-3 worden uitgelezen bestaat de seriële code van dit blok uit negen 9 cellen die niet gelijk zijn aan nul en nadien uit 55 nullen. Met dergelijke gegevens kunnen de bekende compressie-algoritmen wel overweg! 

De run length codering 

Een eerste stap bij het reduceren van al deze nullen is de zogenoemde 'run length codering'. Een data wordt voorgesteld door acht bits, onder de vorm van RRRR-SSSS. In de vier R-bits wordt het aantal data gecodeerd dat gelijk is aan nul en voor de te coderen data staat. In de S-bits wordt de waarde van de data binair gecodeerd. In de onderstaande figuur is een voorbeeldje ter verduidelijking gegeven. 

De 'volgorde' geeft de seriële datastroom weer, de 'decimale code' de waarde van een data uit de stroom. Data '001' heeft een waarde van 5. De codering van de R-bits is in dit voorbeeld onduidelijk omdat niet bekend is hoeveel nul-data vooraf gaan. De S-bits worden gecodeerd met 'H-L-H-L', de binaire representatie van het decimale getal '005'. Nadien volgen 9 data die gelijk zijn aan nul. Deze worden niet gecodeerd. Het elfde data heeft '006' als decimale code. Omdat er negen '000'-data vooraf gaan, worden de R-bits gecodeerd met 'H-L-L-H', de binaire code voor 9. De S-bits worden gecodeerd als 'L-H-H-L', de binaire voorstelling van de decimale code '006'. Dank zij deze codering worden de lange '000'-stromen heel efficiënt gecodeerd is slechts één byte, hetgeen een zeer grote data-reductie oplevert. 

Het principe van de 'run length codering'. (© 2023 Jos Verstraten)

De entropie-codering via Huffmann 

In de laatste stap van het MP3-algoritme worden de run length bytes onderworpen aan een zogenoemde 'entropie-codering' volgens Huffmann. Bij de Huffmann-codering wordt een seriële datastroom beetje bij beetje onderzocht op het statistisch voorkomen van bepaalde codes. Codes die het vaakst aanwezig zijn worden nadien gecodeerd met slechts twee bits. Codes die iets minder vaak aanwezig zijn worden gecodeerd met drie bits. De code die het minst aanwezig is wordt gecodeerd met de langste binaire code die het algoritme toelaat.

Een en ander wordt toegelicht aan de hand van de onderstaande figuur. In dit voorbeeld komt de code 'L-L-L-L-L-L-L-H' blijkbaar het vaakst voor in het onderzochte deel van de seriële datastroom en wordt gecodeerd met slechts twee bits 'L-L'. De code 'L-L-L-L-H-L-H-L' komt het minst vaak voor en wordt gecodeerd met 16 bits. Uiteraard is het noodzakelijk dat per onderzocht deel van de data-stroom een 'code-conversie' wordt genoteerd. Dat kost natuurlijk extra bits, maar dit weegt niet op tegen de reductie in codering van de datastroom. 

Het zal duidelijk zijn dat ook dit systeem een grote datareductie tot gevolg heeft. 

De RRRR-SSSS codes van de run length codering, ieder goed voor acht bits, worden via Huffmann omgezet in codes die gemiddeld genomen veel korter zijn.

Het principe van de 'entropie-codering'. (© 2023 Jos Verstraten)

Bandbreedte-begrenzing

Nog veel meer data-reductie noodzakelijk!

De combinatie van alle beschreven technieken levert een data-reductie om met gemiddeld een factor 13. De WAV-stroom met zijn snelheid van 1,4 Mb/s kan dus gereduceerd worden tot gemiddeld 107 kb/s. Omdat echter de ingewikkelde signaalbewerkingen alleen terug berekend kunnen worden als er in de datastroom ook nog eens allerlei conversiegegevens worden opgenomen, moet u in de praktijk rekenen met een gemiddelde datastroom van 125 kb/s.

In sommige technisch nog niet hoogstaande landen worden echter nog ouderwetse communicatiemedia gebruikt, zoals ISDN of internet via een telefoonmodem. Deze datastroom is dan toch nog te groot. Ook voor sommige zuiver militaire transmissie-systemen, zoals communicatie via extreem lange golven naar onderzeeërs, is deze snelheid onhaalbaar.

Vandaar dat als laatste compressie-systeem een radicale frequentie-begrenzing van het audiosignaal is ingevoerd. MP3 levert in de allerhoogste kwaliteit met 125 kb/s een audio bandbreedte van 20 Hz tot 20 kHz. Door het frequentiebereik aan de hoge kant te beperken kan men een laatste data-reductie tot stand brengen, maar uiteraard gaat dit wél ten koste van de geluidskwaliteit.

Zes kwaliteitsstandaarden 

De ontwerpers van MP3 hebben dan ook zes kwaliteitsstandaarden gespecificeerd, die ieder het geluidsspectrum slechts tot een bepaalde maximale frequentie doorlaten en die ieder een maximale bitrate en een specifiek toepassingsgebied hebben: 

Telephone sound

       - Mode: mono 

       - Maximale frequentie: 2,5 kHz 

       - Maximale bitrate: 8 kb/s (!) 

       - Maximale data-compressie: 96/1 (!) 

       - Toepassing: spraak in telefoon kwaliteit in real time versturen 

Better than shortwave

       - Mode: mono 

       - Maximale frequentie: 4,5 kHz 

       - Maximale bitrate: 16 kb/s 

       - Maximale data-compressie: 48/1 

       - Toepassing: muziek van slechte kwaliteit

Better than AM-radio 

       - Mode: mono 

       - Maximale frequentie: 7,5 kHz 

       - Maximale bitrate: 32 kb/s 

       - Maximale data-compressie: 24/1 

       - Toepassing: geluid van betere kwaliteit 

Similar to FM-radio 

       - Mode: stereo 

       - Maximale frequentie: 11 kHz

       - Maximale bitrate: 64 kb/s 

       - Maximale data-compressie: 26/1 

       - Toepassing: snel downloaden van muziek-clip's

Near-CD

       - Mode: stereo 

       - Maximale frequentie: 15 kHz 

       - Maximale bitrate: 96 kb/s 

       - Maximale data-compressie: 16/1 

       - Toepassing: uitstekende muziekkwaliteit

Compact Disc

       - Mode: stereo 

       - Maximale frequentie: >15 kHz 

       - Maximale bitrate: 128 kb/s 

       - Maximale data-compressie: 14/1 

       - Toepassing: professionele audio-toepassingen

Uitbreidingen en verfijningen

Inleiding

De originele MP3-standaard houdt zich uitsluitend bezig met het op een zo efficiënt mogelijke manier versturen van kwalitatief hoogwaardige stereo-audio. In de loop der jaren is er een aantal uitbreidingen, verfijningen en extra's verzonnen, waardoor er nu eerder sprake is van een open standaard dan van een standaard die in beton is gegoten. Die extra's zitten zo in de datastroom verwerkt dat decoders die niet met deze extra informatie om kunnen gaan die informatie gewoon negeren. Het gevolg is dat zelfs moderne MP3-bestanden door oude MP3-spelers kunnen worden afgespeeld.

De MP3-tag ID3V1

Een van de belangrijkste uitbreidingen is de introductie van de zogenoemde 'MP3-tag ID3'. In die tag kan men een heleboel metadata van het nummer opnemen, waaronder foto's van de cover van het album, de zanger of zangeres, release-datum, uitgeverij, etc. De eerste MP3-tag, ID3V1, werd in 1996 aan het formaat toegevoegd en bevatte slechts 128 bytes. Deze werden aan het einde van het bestand toegevoegd, vooraf gegaan door het woord 'TAG'. 

De tag heeft slechts een ruimte van drie maal 30 bytes beschikbaar voor de titel, de artiest, en de naam van het album. Namen en titels langer dan 30 tekens worden afgekapt. Daarnaast zijn 4 bytes gereserveerd voor het jaar en één byte om het genre van de muziek aan te geven. Men heeft een lijst opgesteld van 80 soorten muziek, in een latere versie werd deze lijst uitgebreid naar 128 soorten. De namen zijn Engelstalig en soms ver gezocht. Zo is er een categorie 'Christian Rap' opgenomen.

Een beperking van de eerste versie van de tag is dat uitsluitend door ISO 8859-1 gedefinieerde karakters zijn toegelaten en dat de internationale tekenset Unicode dus niet wordt ondersteund. Een nadeel van ID3V1 is dat de gegevens aan het einde van de datastroom worden opgenomen. Toen streaming audio doorbrak moest dus eerst het gehele nummers gestreamd worden alvorens de decoder de TAG-gegevens kon uitlezen en aan de gebruiker tonen.

De MP3-tag ID3V2.x

Om aan deze bezwaren tegemoet te komen werd in 1998 een uitgebreide MP3-tag, namelijk ID3V2.x, ontworpen. Deze staat aan het begin van het bestand en wordt dus bij streaming als eerste uitgelezen. Op het moment dat de échte audio-data binnen komen zijn de tag-gegevens al uitgelezen en staan op het schermpje van de MP3-speler. Bovendien is de lengte van de tag flexibel, zodat iedere uitgever zélf kan beslissen welke gegevens er in een bestand worden opgenomen. Om dat gestructureerd te doen is de tag ingedeeld in een aantal frames. Ieder frame kan niet minder dan 16 Mb lang zijn. Op deze manier is het mogelijk niet alleen teksten, maar ook afbeeldingen en zelfs video's in het MP3-bestand onder te brengen. Ieder frame heeft een bepaalde standaard naam, zodat iedere MP3-decoder in staat is de juiste gegevens te interpreteren. Bekende frames zijn bijvoorbeeld:

• TIT2:
  Bevat de titel van het nummer.
• WOAR:
  Bevat de URL van de website van de artiest.
• TLEN:
  Definieert de lengte van de audio.
• AENC:
  Definieert het encryptieschema voor het geluid.
• ReplayGain:
  Definieert de luidheid van een MP3-bestand, deze informatie wordt in sommige geavanceerde MP3-spelers gebruikt om alle MP3-nummers met een identiek volume af te spelen.
• USLT:
  Bevat de uitgeschreven songtekst.

Van deze MP3-tag zijn tot nu toe drie versies verschenen: ID3v2.2, ID3v2.3 en ID3v2.4. Deze laatste werd in november 2000 uitgebracht. Iedere nieuwe versie biedt weer nieuwe mogelijkheden, die echter lang niet allemaal door de bekende MP3-spelers worden ondersteund. De versies ID3v2.3 en ID3v2.4 bieden bijvoorbeeld de mogelijkheid podcasts in het bestand te verwerken.

Herkenning van de MP3-tags

De software die een MP3-bestand ontvangt en omzet naar muziek moet uiteraard in staat zijn een tag-frame te herkennen. In de header van ieder frame zijn elf opeenvolgende 'H'-bits opgenomen, een woord waarvan vrijwel zeker is dat het nooit elders zal voorkomen.

ID3-tags uitlezen en bewerken

Windows biedt de mogelijkheid de ID3-tags die in een MP3-bestand aanwezig zijn uit te lezen en te bewerken. Dat gaat heel eenvoudig. Ga met de muiscursor op de naam van een MP3-bestand staan en klik met de rechter muisknop. Kies uit het pop-up menu 'Eigenschappen'. In het venster dat dan verschijnt kiest u 'Details'. Hier ziet u de in het bestand voorkomende tags met hun inhoud. Sommige inhouden kunt u zélf wijzigen, anderen niet.

De inhouden van MP3-tags in een Windows-venster.
(© 2023 Jos Verstraten)

MP3-bestanden met variabele bitsnelheid

De allereerste MP3-encoders werkten met 'CBR', het letterwoord van 'Constant Bit Rate'. Dat wil zeggen dat de te digitaliseren analoge audio met een constante snelheid werd gesampled. Uiteraard heeft dit systeem hetzelfde bezwaar dat ook geldt voor WAV en Audio-CD. Er zijn stille passages in muziek waar er zo weinig gebeurt dat de sampling snelheid zonder kwaliteitsverlies gereduceerd zou kunnen worden. Het samplen met de standaard constante snelheid kost dan veel bits die niet noodzakelijk zijn.

Vandaar dat het MP3 algoritme zo is aangepast dat er kan worden gewerkt met 'VBR', 'Variable Bit Rate'. De software beschikt over een geheugen waarin diverse frames van de muziek worden opgeslagen. Deze frames worden onderzocht in de mate waarin zij 'levendig' zijn. Een frame waarin erg veel gebeurt wordt dan met een hoge bitrate gesampled, een frame waarin weinig gebeurt wordt met een veel lagere bitrate gesampled. De gekozen sampling rate wordt in de header van ieder afzonderlijk MP3 audioframe opgeslagen, zodat de MP3-decoder weet met welke snelheid ieder frame werd gedigitaliseerd.

MP3HD

Door het Franse 'Thomson SARL' werd in maart 2009 een versie van MP3 ontwikkeld die in één bestand twee versies van de audio bevat. De ene versie is volledig compatibel met de MP3 standaard en werk dus met een lossy compressie. Daarnaast is een tweede datastroom aanwezig waarin wél wordt gecomprimeerd maar op een verliesvrije (lossless) manier. Dat wil zeggen dat er geen gegevens van het originele audiobestand verloren gaan. De verliesvrije MP3HD-stream zorgt dus, na decodering, voor een volledig bit-exacte kopie van de originele audiotracks van audio-CD of WAV. De gemiddelde bitrates variëren tussen 500 kbit/s en 900 kbit/s, afhankelijk van het genre.

De verliesvrije data worden geplaatst in de ID3-metagegevens, zodat een rudimentaire MP3-speler deze gegevens negeert.

MP3HD wordt ondersteund door Winamp met een speciale plug-in en door de Windows Media Player met het 'DirectShow'-filter.



(Banggood sponsor advertentie)
278 Pcs Polyester Film Capacitors