|
Waarschijnlijk bent u er zich niet van bewust, maar de kans is groot dat de elektronica in uw wasmachine werkt met een techniek die 'fuzzy logic' of 'vage logica' heet. 
|
Inleiding tot de fuzzy logic
Begrenzingen van harde logica
Met de toenemende complexiteit van de automatisering van de elektronica wordt men steeds vaker geconfronteerd met het gegeven dat bepaalde processen niet zo gemakkelijk te vangen zijn in harde logica. In zelfs de meest eenvoudige huishoudelijke apparaten, zoals wasmachines en thermostaten, zitten tegenwoordig microprocessors of -controllers. Maar die chip's eisen wél keiharde logica, zowel in hun invoergegevens als in hun beslissingen. Deze beslissingsregels, waarmee de processor uit de invoergegevens bepaalde uitvoergegevens afleidt, moeten volledig en ondubbelzinnig bepaald zijn. Met de beslissingsregel 'als de was in het wasmachine iets droger is dan normaal, dan moet de centrifugetijd iets korter worden' kan een microcontroller helemaal niets beginnen. Natuurlijk zou een dergelijk probleem nog wel omgezet kunnen worden in keiharde logica door de vochtigheidsgraad van de was te meten.
De toegepaste regelingen worden echter steeds ingewikkelder. Soms hebben tientallen ingangsgrootheden invloed op een proces. Bovendien gaat een factor, namelijk de ervaring van de menselijke procesbegeleider, steeds meer invloed hebben op het eindresultaat.
Fuzzy logic of vage logica
Vandaar dat reeds in de jaren zeventig van de vorige eeuw een geheel nieuwe benadering van dergelijke problemen werd gezocht. Alle elementen van een verzameling worden nu niet in twee keiharde set's ingedeeld ('JA' en 'NEE') maar volgens een glijdende schaal van '0 % JA' (en dus '100 % NEE') tot '100 % JA' (en dus '0 % NEE'). Een dergelijke benadering sluit veel beter aan bij de manier waarop mensen met informatie omgaan.
Nu mag u niet de vergissing begaan om te denken dat in- en uitvoergegevens niet meer feitelijk hard zijn! Er is weinig vaags aan de vage logica! De kunst van het principe is de in- en uitgangsgegevens te vangen in zogenoemde 'lidmaatschapsfuncties' en nadien beslissingsregels op te stellen waarmee het systeem uit de voeten kan.
Lotti Zadeh
De fundamenten van de vage logica zijn, zoals met veel moderne technieken het geval is, terug te vinden in de theoretische wiskunde. In 1965 publiceerde de wiskundige L. A. Zadeh van de Berkeley universiteit in de Verenigde Staten een boek, getiteld 'Fuzzy Sets in Information and Control'. De bedoeling was een wiskundige theorie op te stellen waarmee taalkundige stellingen vertaald konden worden naar wiskundige formules.
Het was Zadeh onmiddellijk duidelijk dat dit alleen maar kon als werd afgeweken van de klassieke verzamelingsleer, waarbij een element ondubbelzinnig tot een set behoort. Vandaar voerde hij het begrip 'lidmaatschapsgraad' in, waarmee wordt aangegeven in hoeverre een bepaald element van de verzameling tot een bepaalde set behoort. Deze lidmaatschapsgraad kan dan worden omgezet in een 'lidmaatschapsfunctie', afgekort tot 'LF'. Dat is in wezen niets anders dan een grafische voorstelling van de graad van lidmaatschap van ieder element uit de verzameling bij een bepaalde set.
Op deze manier worden alle ingangsvariabelen omgezet in een of meerdere LF's. Dit proces noemt men de 'fuzzificatie'. Ook de uitgangsvariabelen moeten op een identieke manier gefuzzificeerd worden. Nadien moeten bepaalde relaties tussen deze in- en uitgangsgrootheden worden opgesteld. Dit noemt men het 'redeneermechanisme'. De regels voor dit redeneermechanisme worden ontleend uit de kennis die de bedenker van het systeem heeft. Vandaar dat vaak wordt gerefereerd naar de 'kennisbank' en de regels 'ervaringsregels' worden genoemd.
De laatste stap noemt men de 'defuzzificatie'. Hierin worden de LF's van de ingangsgrootheden en van de uitgangsgrootheden gekoppeld aan de ervaringsregels, met als gevolg dat er bepaalde uitgangsfuncties ontstaan.
Algemene structuur van een fuzzy-regel
Dit proces gebeurt in regels, die welbekend zijn uit de harde logica. De meest algemene structuur van een dergelijke regel is:
ALS
aan bepaalde voorwaarden voldaan wordt
DAN
moet op een bepaalde manier een actie worden ondernomen
Het enige verschil is dat de voorwaarden en de acties niet alleen 'JA' en 'NEE' kunnen zijn, maar ook tussenwaarden kunnen hebben.
Het fuzzy-proces
Het volledige proces van fuzzy logic kan dus voorgesteld worden zoals samengevat in de onderstaande figuur:
- Fuzzificatie
Ingangsgrootheden en uitgangsgrootheden worden verwerkt tot lidmaatschapsfuncties, waarbij rekening wordt gehouden met ervaringsregels die in de kennisbank aanwezig zijn. - Redeneermechanisme
Hierbij is het de bedoeling een aantal ALS . . . DAN regels op te stellen waarbij de vage ingangsvariabelen gekoppeld worden aan een of meerdere vage uitgangsvariabelen. Deze regels beschrijven het proces waarop het fuzzy-proces wordt toegepast. - Inferentie
De inferentie is de techniek van het redeneermechanisme, waarmee de fuzzy-processor uit de opgestelde regels een bepaalde uitgangsfunctie afleidt. - Defuzzificatie
Uit de regels worden waarden voor de uitgangsvariabelen afgeleid, die niet langer vaag zijn maar concreet, zodat elektronische schakelingen er weer iets mee kunnen aanvangen.
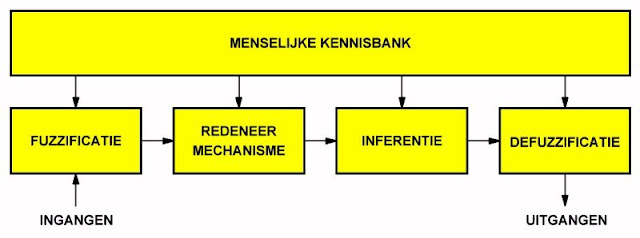 |
| De vier voornaamste stappen van een fuzzy-proces samengevat. (© 2021 Jos Verstraten) |
Specifieke toepassingsterreinen van vage logica
Vage logica wordt toegepast in die processen die met harde logica heel moeilijk te omschrijven zijn. Een typisch voorbeeld van een dergelijk proces is patroonherkenning. Patroonherkenning staat uiteraard in het middelpunt van de belangstelling, het vormt immers het kloppend hart van zeer uiteenlopende praktisch toepassingen zoals:
- elektronische handschrift herkenning
- elektronische spraak herkenning
- verminkte gegevens terugwinnen uit beschadigde datastromen
- automatische sorteersystemen, zoals het sorteren van tomaten op grootte
- automatische visuele inspectie door middel van een video-camera
Al deze toepassingen hebben een belangrijke eigenschap gemeen en dat is dat de ingangsvariabelen niet exact omschreven kunnen worden. Het heeft geen zin om te proberen vorm en kleur van een tomaat wiskundig te beschrijven in exacte formules. Iedere tomaat zal immers in min of meerdere mate van een dergelijke absolute beschrijving afwijken. Hier kunnen alleen de vage beslissingen van de vage logica bruikbare oplossingen bieden.
De fuzzificatie in detail
Het principe van de lidmaatschapsfunctie
Zoals reeds geschreven is het voornaamste instrument van de vage logica de 'lidmaatschapsfunctie' LF, in het Engels 'membership function' genoemd en in het Duits 'Zugehörigkeitsfunktion'. Soms wordt in het Nederlands ook de term 'toebehorenfunctie' gebruikt. Het woord lidmaatschap dekt echter veel beter de lading en vandaar dat deze in dit artikel gebruikt zal worden. De lidmaatschapsfunctie is een grafiek die aangeeft in hoeverre een bepaald element uit een verzameling tot een bepaalde set behoort.
Een voorbeeldje zal dit verduidelijken. Stel dat u aan duizend personen de vraag stelt aan welke leeftijd men denkt als men het begrip 'een jonge man' in gedachten neemt. Waarschijnlijk zal er één leeftijd het vaakst worden genoemd worden, bijvoorbeeld '25 jaar'. Rond deze vaakst genoemde leeftijd zullen antwoorden liggen die iets minder vaak genoemd worden. zoals '24 jaar' en '26 jaar'. Tot slot zullen er ook antwoorden zijn die maar door een paar mensen worden genoemd, zoals '40 jaar' en '10 jaar'.
U kunt nu aan de meest genoemde leeftijd een waarde 1 toekennen en alle andere leeftijden hieraan relateren. Als het antwoord '25 jaar' 120 keer wordt genoemd en het antwoord '15 jaar' 12 keer, dan relateert u het antwoord '15 jaar' aan het antwoord '25 jaar' door er de waarde 0,1 aan toe te kennen.
U bent nu klaar voor het opstellen van de lidmaatschapsfunctie voor het begrip 'een jonge man'. Die functie bestaat uit de grafiek die getekend is in de onderstaande figuur. Op de verticale as worden alle aan het antwoord '25 jaar' gerelateerde getallen uitgezet, op de horizontale as alle verkregen antwoorden. Het resultaat is een Gaussiaanse verdelingscurve.
Een lidmaatschapsfunctie heeft dus steeds een verticale as die van 0 tot 1 loopt. De indeling en schaal van de horizontale as is afhankelijk van het verschijnsel dat u wilt fuzzificeren.
 |
| De lidmaatschapsfunctie voor het begrip 'een jonge man'. (© 2021 Jos Verstraten) |
Nog wat nieuwe begrippen
Aan de hand van de definitie van een lidmaatschapsfunctie kunnen wij nog enige nieuwe begrippen definiëren:
- kwantificatie
- lidmaatschapsgraad
- fuzzy-set
- linguïstische variabele
- tolerantie.
Kwantificatie
Wat in de bovenstaande figuur is gebeurd, is dat een vaag begrip als 'een jonge man' gekwantificeerd is. Er worden waarden aan toegekend, waardoor het voor een marsmannetje mogelijk wordt een relatie te leggen tussen leeftijden van aardbewoners en het begrip 'een jonge man', zelfs zonder dat hij ooit een aardbewoner heeft gezien.
Lidmaatschapsgraad
Aan de hand van de lidmaatschapsfunctie kunt u aan iedere leeftijd een zogenoemde lidmaatschapsgraad toekennen. Deze graad wordt standaard voorgesteld door μ. In het voorbeeld is de lidmaatschapsgraad van het antwoord '25 jaar' gelijk aan 1. Het zal duidelijk zijn dat de waarde van μ steeds wordt begrensd door het minimum 0 en het maximum 1.
Fuzzy-set
Het volledig bereik van de lidmaatschapsfunctie noemt men de 'fuzzy-set'. De bovenstaande figuur geeft dus de fuzzy-set voor het vage begrip 'een jonge man'.
Linguïstische variabele
Het vage begrip waarvoor u een fuzzy-set opstelt wordt 'linguïstische variabele' genoemd. Het is een variabele omdat u er verschillende waarden van μ uit kunt afleiden. Het is een linguïstische variabele, omdat de kwantificering ervan niet wiskundig exact is, maar taalkundig gedefinieerd wordt.
Wiskundige vergelijkingen zoeken
Ook in de vage logica moet gerekend worden, want er moeten immers uitgangsgrootheden worden afgeleid uit de ingangsgrootheden. Rekenen aan ingangsgrootheden kan alleen als u het verloop van deze grootheden in exacte wiskundige formules kunt vastleggen. Met andere woorden: u moet aan iedere lidmaatschapsfunctie een wiskundige vergelijking koppelen, die de functie zo goed mogelijk beschrijft.
De algemene vorm van een dergelijke vergelijking is:
μA(x) = wiskundige uitdrukking
waarbij x een bepaald element uit de vage verzameling is van de linguïstische variabele A. In het voorbeeld zou x bijvoorbeeld gelijk kunnen zijn aan '21 jaar', terwijl A natuurlijk gelijk is aan 'een jonge man'.
De tolerantie
Nu is het vrij ingewikkeld om de Gaussiaanse klokfunctie van het voorbeeld op een simpele manier om te zetten in een wiskundige uitdrukking. Vandaar dat in de meeste gevallen de opgestelde lidmaatschapsfuncties worden vereenvoudigd. De mate van vereenvoudiging wordt de 'tolerantie' genoemd. De lidmaatschapsfunctie van de linguïstische variabele 'een jonge man' kunt u bijvoorbeeld vereenvoudigen tot de onderstaande figuur. Dat is een driehoekvorm die u gemakkelijk in een wiskundige formule kunt omzetten.|
 |
| De lidmaatschapsfunctie wordt vereenvoudigd tot een driehoekvorm. (© 2021 Jos Verstraten) |
Soorten lidmaatschapsfuncties
Vereenvoudiging gewenst
In de meeste gevallen kunt u de lidmaatschapsfuncties vereenvoudigen tot:
- lineaire functies
- gesegmenteerde lineaire functies
- S-, PI- en Z-functies
- Singletons
Lineaire functies
Het beschreven proces noemt men de 'lineaire fuzzificering' en de daaruit volgende lidmaatschapsfuncties 'lineaire functies'. Nogal logisch, want de lidmaatschapsfunctie bestaat nu nog slechts uit rechte lijntjes.

Gesegmenteerde lineaire functies
De tolerantie in bij lineaire functies vrij groot. U kunt het ook iets nauwkeuriger doen, door de Gaussiaanse klokfunctie te benaderen door middel van drie of zelfs zeven rechte lijnstukken, die de curve zo goed mogelijk benaderen. Dan ontstaan de LF's die voorgesteld worden in de onderstaande figuur. Dergelijke benaderingen noemt men 'gesegmenteerde lineaire lidmaatschapsfuncties'. De oorsprong van deze benaming is duidelijk. De functie bestaat nu immers uit een aantal rechte segmenten.
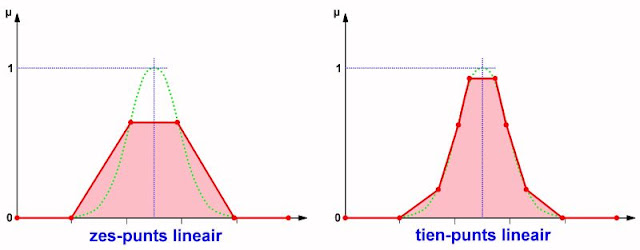 |
| De tolerantie neemt af als u werkt met gesegmenteerde lineaire lidmaatschapsfuncties. (© 2021 Jos Verstraten) |
S-, PI- en Z-functies
Naast de al dan niet gesegmenteerde lineaire lidmaatschapsfuncties worden in de praktijk ook zogenoemde kwadratische functies toegepast. Er zijn drie standaardvormen, getekend in de onderstaande figuur. De S-, PI- en Z-functie kunnen alle drie met dezelfde vrij eenvoudige wiskundige kwadratische vergelijkingen worden beschreven.
 |
| De drie standaardvormen van de kwadratische lidmaatschapsfunctie. (© 2021 Jos Verstraten) |
De singleton
Een speciale lineaire lidmaatschapsfunctie is de singleton. Een singleton, voorgesteld in de onderstaande figuur, heeft slechts één lid van de vage verzameling, waarvoor μ een waarde heeft die niet nul is. Uit de aard der zaak moet deze waarde dan gelijk zijn aan 1. In feite is er aan een singleton niets vaags te ontdekken en zou een dergelijke verzameling zich heel goed thuis voelen in de harde logica. Het begrip singleton is in de vage logica ingevoerd, omdat men nu eenmaal soms te maken heeft met variabelen die maar één waarde kunnen hebben. Een typisch voorbeeld van een linguïstische variabele, die alleen maar door middel van een singleton functie is uit te drukken is 'noem de dag van de week die overeen komt met de datum 12 maart 2021'. Hierop is maar één antwoord mogelijk, namelijk 'vrijdag'. Als de grafiek de lidmaatschapsfunctie van deze linguïstische variabele zou voorstellen, dan zou Xo gelijk zijn aan het antwoord 'vrijdag'.
Uit de aard der zaak is lidmaatschapsgraad μXo gelijk aan 1.
 |
| De singleton lidmaatschapsfunctie. (© 2021 Jos Verstraten) |
Verfijnen van de lidmaatschapsfunctie
Termen en hedges
De vage logica heeft een aantal begrippen ingevoerd waarmee het mogelijk wordt lidmaatschapsfuncties beter te definiëren. De voornaamste verfijningen zijn:
- termen
- hedges
Termen
Termen zijn bijvoeglijke naamwoorden die aan de linguïstische variabele worden gekoppeld. Ook dit begrip kan het best aan de hand van een voorbeeld worden uitgediept worden. Stel de linguïstische variabele 'kamertemperatuur'. Dat is een zeer vaag begrip dat echter beter gedefinieerd kan worden door er enige bijvoeglijke naamwoorden of termen aan te koppelen. U kunt de kamertemperatuur kunnen omschrijven als:
- koud
- koel
- aangenaam
- warm
- heet
Als u nu aan duizend personen een lijstje zou overhandigen met daarin ingevuld temperaturen van 10 °C tot 32 °C en zou vragen aan iedere temperatuur een van de bovenstaande vijf termen te koppelen, dan zouden vijf vage verzamelingen ontstaan, die allemaal op de beschreven manier omgezet kunnen worden in een lidmaatschapsfunctie. Men kan deze vijf LF's verzamelen in één grafiek, met als gevolg dat de onderstaande figuur ontstaat.
Merk op dat bepaalde temperaturen nu deel uitmaken van verschillende verzamelingen. Dat is een zeer fundamenteel verschil tussen de harde logica en de vage logica! De temperatuur '20 °C' maakt bijvoorbeeld deel uit van de verzameling 'aangenaam', maar ook van de verzameling 'koel'. Aan deze temperatuur kunt u dus een μaangenaam en een μkoel koppelen.
In de traditionele harde logica is het absoluut ondenkbaar dat een element deel uitmaakt van twee verzamelingen.
 |
| De lidmaatschapsfuncties van vijf termen van de linguïstische variabele 'kamertemperatuur'. (© 2021 Jos Verstraten) |
Dé kracht van de vage logica
Het feit dat een element deel kan uitmaken van meer dan één vage verzameling is dé kracht van de vage logica. Door linguïstische variabelen om te zetten in lidmaatschapsfuncties van een aantal termen, ontstaat een zeer verfijnd beeld van de variabele, een beeld dat als het ware op een menselijke manier met de variabele omgaat. Hierdoor kunnen regelsystemen als het ware natuurlijk afgestemd worden op het menselijk gedrag.
Hedges
In taalkundige termen uitgedrukt kunt u hedges opvatten als bijwoorden, die aan de termen van de linguïstische variabele worden gekoppeld. U kunt de term 'koel' van de linguïstische variabele 'kamertemperatuur' bijvoorbeeld nader specificeren met de hedges 'een beetje' en 'zeer'. Er ontstaan dan twee tamelijk nauwkeurige linguïstische begrippen, namelijk 'een beetje koele kamertemperatuur' en 'zeer koele kamertemperatuur'. Dank zij deze hedges kan de ontwerper van een vaag regelsysteem ingrijpen in de lidmaatschapsfuncties. Het zal immers duidelijk zijn dat het invoeren van hedges invloed heeft op de vorm van de lidmaatschapsfuncties.
Hedges worden vaak ingevoerd in de testfase van een vaag regelsysteem. Als dan blijkt dat de opgestelde lidmaatschapsfuncties van de in- en uitgangsgrootheden toch niet het gewenste regeleffect veroorzaken, dan kan men het systeem verfijnen door de lidmaatschapsfuncties iets aan te passen door het invoeren van een of meerdere hedges.
Hiervoor zijn twee benaderingen mogelijk:
- shifted hedges
- powered hedges
Shifted hedges
Een shifted hedge doet niets anders dan de grenzen van de lidmaatschapsfunctie van de term naar links of naar rechts verschuiven. In de onderstaande figuur is aangegeven hoe de hedge 'een beetje' de LF van de term 'koud' naar rechts verschuift.
 |
| De invloed van een shifted hedge. (© 2021 Jos Verstraten) |
Powered hedge
Bij de powered hedge worden de grenzen van de lidmaatschapsfunctie niet verschoven, maar wordt de vorm aangepast. In de onderstaande figuur is getekend hoe door het invoeren van de powered hedge 'zeer' in de term 'koud' de lidmaatschapsfunctie zo wordt aangepast dat lagere temperaturen in de verzameling 'koud' een minder dan lineaire toename van hun μ krijgen. Een bepaalde temperatuur X heeft zonder de hedge een μ van ongeveer 0,5. Door het invoeren van de powered hedge daalt zijn lidmaatschapsgraad μ tot ongeveer 0,2.
 |
| De invloed van een powered hedge. (© 2021 Jos Verstraten) |
Het redeneermechanisme
Inleiding
Doel van het redeneermechanisme is een aantal regels opstellen die de gewenste relatie tussen de ingangs- en de uitgangsgrootheden vast leggen. In principe wijkt deze stap niet al van het opstellen van de beslissingsregels in de harde logica. Het enig verschil is dat de beslissingsregels in de vage logica minder hard zijn en meer aangepast aan de menselijke subjectieve maatstaven.
De meest algemene vorm van een vage beslissingsregel is:
ALS premisse DAN conclusie
Premisse
De premisse bestaat uit een of meer uitspraken, 'antecedenten' genoemd, die betrekking hebben op de ingangsgrootheden. Een voorbeeld van een premisse is:
kamertemperatuur IS warm EN buitentemperatuur IS koel
Twee linguïstische ingangsvariabelen 'kamertemperatuur' en 'buitentemperatuur' worden hierin nader omschreven door hun termen 'warm' en 'koel' en door middel van een fuzzy-operator EN aan elkaar gekoppeld.
De premisse geeft dus als het ware aan welke lidmaatschapsfuncties van de ingangsgrootheden in de regel actief zijn. Bij het uitwerken van deze regel zal de fuzzy-processor de actuele waarden van de twee ingangsgrootheden meten, deze op de assenstelsels van de LF's zetten en de μ's berekenen van de actieve lidmaatschapsfuncties. Deze twee waarden van μ worden dan gebruikt om de uitgangsvariabele te berekenen.
Conclusie
De conclusie heeft op dezelfde manier betrekking op de uitgangsgrootheden. In het voorbeeld:
motorsnelheid IS hoog
wordt de LF van term 'hoog' van de linguïstische uitgangsvariabele 'motorsnelheid' geactiveerd. De berekende μ's van de actieve ingangs-LF's worden aan de geselecteerde uitgangs-LF aangeboden en er wordt op een bepaalde manier een specifieke waarde voor de uitgangsvariabele berekend. Op dit rekenmechanisme wordt later nader ingegaan.
Voorbeeld van premisse en conclusie
Aan de hand van een voorbeeldje wordt de praktische betekenis van premisse en conclusie toegelicht. Stel dat een bepaald systeem een uitgangsvariabele X heeft, die op een bepaalde manier moet reageren op de waarde van twee ingangsvariabelen A en B. Volgens de regels van de fuzzy logic worden deze drie linguïstische grootheden nader gespecificeerd door termen:
- Ingangsvariabele A
Kan ingedeeld worden in de drie termen 'laag', 'normaal' en 'hoog'. - Ingangsvariabele B
Krijgt ook drie termen, namelijk 'klein', 'normaal' en 'groot'. - Uitgangsvariabele X
Wordt met de termen 'snel' en 'traag' beschreven.
 |
Grafische toelichting van de reële betekenis van de premisse en de conclusie. |
Vervolgens maakt u een vage beslissingsregel:
ALS A IS hoog EN B IS normaal DAN X IS traag
Het fuzzy-systeem weet nu dat bij de uitwerking van deze regel het rekening moet houden met de LF van 'A-hoog' en de LF van 'B-normaal'. De overige LF's van de ingangsvariabelen zijn niet aan de orde. Het resultaat zal uitgelezen moeten worden in de LF van 'X-traag'. Hoe dat in- en uitlezen gaat wordt later besproken.
U kunt nu voor dit systeem een tweede vage beslissingsregel opstellen, bijvoorbeeld:
ALS A IS normaal EN B IS groot, DAN X is snel
In de onderstaande figuur is getekend welke lidmaatschapsfuncties nu actief worden.
 |
| De actieve LF's voor de vage regel 'Als A is normaal EN B is groot, DAN X is snel'. (© 2021 Jos Verstraten) |
Verfijningen
Uiteraard stelt de theorie een aantal verfijningen voor, waardoor een beslissingsregel veel nauwkeuriger het verband tussen de in- en uitgangsgrootheden kan vastleggen. De voornaamste verfijningen zijn:
- fuzzy-operatoren
- evaluerende regels
- voorspellende regels
Fuzzy-operatoren
Net zoals de harde Booleaanse algebra kent ook het rekenstelsel van de fuzzy logic een aantal operatoren, te weten:
- EN
- OF
- NIET
U kunt deze operatoren opnemen in een premisse om de onderlinge relatie tussen de ingangsgrootheden beter te omschrijven.
De EN-operator
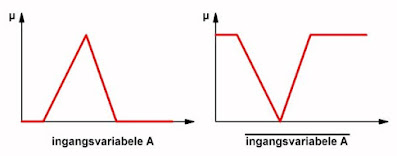
De EN-operator laat toe twee lidmaatschapsfuncties van een variabele actief te maken in één beslissingsregel. Zoals uit de onderstaande figuur blijkt, zal bij een EN-koppeling alleen het gemeenschappelijk oppervlak van beide LF's actief worden. De figuur geeft het resultaat van:
ALS A IS klein EN A is groot DAN .....
Natuurlijk wordt de EN-operator ook gebruikt om twee ingangsvariabelen met elkaar te koppelen, zoals in:
Als A is groot EN B IS klein DAN .....
In dit geval zal de kleinste μ-waarde van beide LF's in de berekening worden betrokken.
Dit wordt toegelicht aan de hand van de onderstaande figuur. De vage beslissingsregel van dit voorbeeld luidt:
ALS A IS normaal EN B IS groot DAN .....
Op het moment dat de fuzzy-processor deze regel verwerkt, meet hij de actuele waarden van de ingangsvariabelen. Deze zijn A1 en B1. Deze worden op de assen van de functies gezet. Hieruit kunt u twee actieve μ-waarden berekenen, een voor A1 (μA1) en een voor B1 (μB1). Omdat A en B in de regel door een EN-operator gekoppeld zijn, zal nu alleen de laagste μ-waarde overgedragen worden naar de uitgangsfunctie voor het berekenen van de actuele waarde van de uitgang. In dit voorbeeld is dit dus duidelijk μA1.
De OF-operator
Ook deze operator laat toe twee LF's van een ingangsvariabele te activeren. In dit geval wordt, zoal getekend in de onderstaande figuur, het gezamenlijk oppervlak van beide LF's geactiveerd. De premisse van dit voorbeeld luidt:
ALS A IS klein OF A IS groot DAN .....
Natuurlijk kunt u de OF-operator ook gebruiken om twee variabelen te koppelen. In de onderstaande figuur is als voorbeeld de premisse:
ALS A IS normaal OF B IS groot DAN .....
gegeven. Ook nu meet de fuzzy-processor de actuele waarden van de ingangen en berekent uit de actieve LF's hun μ-waarden. Maar vanwege de OF-koppeling wordt nu de grootste μ-waarde doorgekoppeld naar de uitgangsfunctie. In dit geval is dit dus μB1.
De NIET-operator
De NIET-operator is de ook in de harde logica bekende inverteerfunctie. Het resultaat van een NIET-operatie is dat alle waarden van μ opnieuw worden berekend volgens de formule:
μĀ(x) = 1 - μA(x)
Met andere woorden: de geïnverteerde waarden μniet van μ kunt u berekenen door de waarden van μ van 1 af te trekken. Wat dit grafisch betekent is voorgesteld in de onderstaande figuur.
 |
| Het resultaat van een EN-operator. (© 2021 Jos Verstraten) |
Natuurlijk wordt de EN-operator ook gebruikt om twee ingangsvariabelen met elkaar te koppelen, zoals in:
Als A is groot EN B IS klein DAN .....
In dit geval zal de kleinste μ-waarde van beide LF's in de berekening worden betrokken.
Dit wordt toegelicht aan de hand van de onderstaande figuur. De vage beslissingsregel van dit voorbeeld luidt:
ALS A IS normaal EN B IS groot DAN .....
Op het moment dat de fuzzy-processor deze regel verwerkt, meet hij de actuele waarden van de ingangsvariabelen. Deze zijn A1 en B1. Deze worden op de assen van de functies gezet. Hieruit kunt u twee actieve μ-waarden berekenen, een voor A1 (μA1) en een voor B1 (μB1). Omdat A en B in de regel door een EN-operator gekoppeld zijn, zal nu alleen de laagste μ-waarde overgedragen worden naar de uitgangsfunctie voor het berekenen van de actuele waarde van de uitgang. In dit voorbeeld is dit dus duidelijk μA1.
 |
| De invloed van de EN-operator op het evalueren van de waarden van de premisse. (© 2021 Jos Verstraten) |
De OF-operator
Ook deze operator laat toe twee LF's van een ingangsvariabele te activeren. In dit geval wordt, zoal getekend in de onderstaande figuur, het gezamenlijk oppervlak van beide LF's geactiveerd. De premisse van dit voorbeeld luidt:
ALS A IS klein OF A IS groot DAN .....
 |
| Het resultaat van een OF-operator. (© 2021 Jos Verstraten) |
Natuurlijk kunt u de OF-operator ook gebruiken om twee variabelen te koppelen. In de onderstaande figuur is als voorbeeld de premisse:
ALS A IS normaal OF B IS groot DAN .....
gegeven. Ook nu meet de fuzzy-processor de actuele waarden van de ingangen en berekent uit de actieve LF's hun μ-waarden. Maar vanwege de OF-koppeling wordt nu de grootste μ-waarde doorgekoppeld naar de uitgangsfunctie. In dit geval is dit dus μB1.
 |
| De invloed van de OF-operator op het evalueren van de waarden van de premisse. (© 2021 Jos Verstraten) |
De NIET-operator
De NIET-operator is de ook in de harde logica bekende inverteerfunctie. Het resultaat van een NIET-operatie is dat alle waarden van μ opnieuw worden berekend volgens de formule:
μĀ(x) = 1 - μA(x)
Met andere woorden: de geïnverteerde waarden μniet van μ kunt u berekenen door de waarden van μ van 1 af te trekken. Wat dit grafisch betekent is voorgesteld in de onderstaande figuur.
Evaluerende regels
Evaluerende regels worden het vaakst toegepast. Alle tot nu toe gebruikte voorbeelden zijn evaluerende regels. De meest algemene uitdrukking van een evaluerende regel is:
ALS A IS a EN/OF B IS b DAN X is x
waarin A en B staan voor ingangsvariabelen, a en b voor hun actieve termen, X voor de uitgangsvariabele en x voor zijn actieve term.
De meeste opdrachten uit de vage logica kunnen uitstekend met evaluerende regels opgelost worden.
Voorspellende regels
Voorspellende regels zijn niet zo gemakkelijk op te stellen, maar zij bieden wel zeer krachtige functies. Een voorbeeld van een voorspellende regel, zuiver onder linguïstische vorm is:
ALS krachtiger remmen bij een gegeven snelheid tot gevolg heeft dat de motor sneller stopt binnen de toegestane afstand, ga DAN krachtige remmen.
Een specifieke eigenschap van voorspellende regels is dat de uitgangsvariabele altijd wordt opgenomen binnen de premisse van de regel. Er kan een aantal voorspellende regels onder elkaar in het programma worden opgenomen. De fuzzy-processor zal deze dan een voor een evalueren en de voorspellende regel die het beste stuursignaal oplevert vervolgens selecteren en uitvoeren.
In termen van fuzzy notatie kunt u een voorspellende regel als volgt noteren:
ALS [X IS x → (A IS a EN/OF B IS b)] DAN X IS x
Inleiding
De inferentie is de techniek van het redeneermechanisme waarmee de fuzzy-processor uit de opgestelde regels een bepaalde uitgangsfunctie afleidt. Deze uitgangsfunctie hangt bovendien af van de momentele waarden van de μ's van de ingangen, maar is nog steeds een vage verzameling die men een fuzzy-functie noemt. Een voorbeeld zal het inferentie-proces verduidelijken.
Voorbeeld
Gegeven is een regelsysteem met twee ingangen A en G en een uitgang X. Ingang A kan beschreven worden in vijf termen, waaronder 'm' en 'n'. Ingang G kan beschreven worden in vijf termen, waaronder 'h'. Uitgang X kan beschreven worden in vijf termen, waaronder 'e' en 'o'. Het te sturen proces kan volledig beschreven worden met twee vage regels:
Regel 1:
ALS A IS m EN G IS h DAN X is e
Regel 2:
ALS A IS n EN G IS h DAN X IS o
Op het moment dat de fuzzy-processor de regels uitwerkt is de actuele waarde van de ingangsgrootheden:
A = 175
G = 190
Het volledige proces van inferentie is samengevat in de onderstaande figuur. De bovenste grafiek geeft de inferentie van de eerste regel. Natuurlijk zijn de LF's 'm' van A en 'h' van G actief, want die staan vermeld in de eerste regel. Uit de actuele waarden 175 en 190 kunnen de twee corresponderende μ-waarden berekend worden, waaruit blijkt dat μA = 0,25 en μG = 1.
Omdat beide variabelen door middel van een EN-operator gekoppeld zijn, telt alleen de laagste μ-waarde, in dit geval 0,25. Deze wordt horizontaal doorgetrokken naar de grafiek van de uitgang X. Hier is de LF van 'e' actief. Er ontstaat nu een nieuwe vage verzameling, die begrensd wordt door de μ-waarde 0,25. Deze fuzzy-functie is gearceerd weergegeven.
De onderste grafiek geeft de inferentie van de tweede regel. Nu is de LF An actief, alsmede de LF van Gh. De waarden van de ingangen zijn natuurlijk nog niet gewijzigd, met als gevolg dat u nu twee μ-waarden van 0,75 en 1 kunt berekenen. Ook nu wordt er gekoppeld met een EN-operator, zodat de laagste μ (0,75) weer wordt doorgetrokken naar de uitgangsgrafiek. Hier is de LF van Xo actief. Ook nu berekent het inferentie-proces een nieuwe vage verzameling, die nu begrensd wordt door de μ-waarde 0,75.
Soorten inferentie
Er zijn verschillende algoritmen ontwikkeld voor het opstellen van fuzzy-functies door middel van inferentie. De meest toegepaste zijn:
- MIN-MAX inferentie
- MAX-PROD inferentie
De verschillen worden toegelicht aan de hand van de onderstaande figuur.
MIN-MAX inferentie
De linker grafiek geeft het resultaat van een MIN-MAX inferentie. De actieve LF van de uitgang wordt begrensd door de actieve waarde van de μ van de ingangen.
MAX-PROD inferentie
De rechter grafiek toont wat er gebeurt als wordt gewerkt volgens het MAX-PROD schema. Nu wordt de actieve LF van de uitgang niet begrensd, maar verkleind in hoogte, tot de top samenvalt met de actieve waarde van μ.

Inferentie-strategieën
Er is geen sprake van een goede inferentie-strategie. Voor sommige toepassingen kunt u het best gebruik maken van de MIN-MAX algoritmen, andere toepassingen geven de beste resultaten als u volgens MAX-PROD werkt. Bovendien zijn er tientallen andere inferentie-strategieën theoretisch uitgewerkt.
De compositie
Door de inferentie wordt iedere regel van het redeneermechanisme omgezet in een fuzzy-functie, die het door de uitgang te volgen gedrag definieert bij bepaalde waarden van de ingangsvariabelen. Natuurlijk hebt u daar in de praktijk vrij weinig aan, want wat moet ontstaan is een eenduidige uitgangsfunctie, waaruit een welbepaalde waarde voor de uitgang kan worden afgeleid. Op de een of andere manier moeten alle afzonderlijke fuzzy-functies van de uitgang worden gecombineerd tot één algemeen geldende functie, die rekening houdt met alle stellingen die in alle regels vastgelegd zijn. Dit proces noemt men de 'compositie'.
In de meeste gevallen gaat dit door de afzonderlijke fuzzy-functies met elkaar te verknopen met een 0R-operator. Dat is vrij logisch, want u kunt er van uitgaan dat het systeem aan alle regels van het redeneermechanisme moet voldoen, hetgeen te vertalen is naar een OR-functie.
In het eerder in dit artikel besproken voorbeeld levert de compositie dus een eenduidige uitgangsfunctie op, die ontstaat door de twee deelfuncties te OR-ren. Hetgeen, zoals reeds beschreven, er op neer komt dat de oppervlakken van de deelfuncties tot één oppervlak worden verenigd. Een en ander wordt grafisch toegelicht in de onderstaande figuur.
Evaluerende regels worden het vaakst toegepast. Alle tot nu toe gebruikte voorbeelden zijn evaluerende regels. De meest algemene uitdrukking van een evaluerende regel is:
ALS A IS a EN/OF B IS b DAN X is x
waarin A en B staan voor ingangsvariabelen, a en b voor hun actieve termen, X voor de uitgangsvariabele en x voor zijn actieve term.
De meeste opdrachten uit de vage logica kunnen uitstekend met evaluerende regels opgelost worden.
Voorspellende regels
Voorspellende regels zijn niet zo gemakkelijk op te stellen, maar zij bieden wel zeer krachtige functies. Een voorbeeld van een voorspellende regel, zuiver onder linguïstische vorm is:
ALS krachtiger remmen bij een gegeven snelheid tot gevolg heeft dat de motor sneller stopt binnen de toegestane afstand, ga DAN krachtige remmen.
Een specifieke eigenschap van voorspellende regels is dat de uitgangsvariabele altijd wordt opgenomen binnen de premisse van de regel. Er kan een aantal voorspellende regels onder elkaar in het programma worden opgenomen. De fuzzy-processor zal deze dan een voor een evalueren en de voorspellende regel die het beste stuursignaal oplevert vervolgens selecteren en uitvoeren.
In termen van fuzzy notatie kunt u een voorspellende regel als volgt noteren:
ALS [X IS x → (A IS a EN/OF B IS b)] DAN X IS x
De inferentie techniek
Inleiding
De inferentie is de techniek van het redeneermechanisme waarmee de fuzzy-processor uit de opgestelde regels een bepaalde uitgangsfunctie afleidt. Deze uitgangsfunctie hangt bovendien af van de momentele waarden van de μ's van de ingangen, maar is nog steeds een vage verzameling die men een fuzzy-functie noemt. Een voorbeeld zal het inferentie-proces verduidelijken.
Voorbeeld
Gegeven is een regelsysteem met twee ingangen A en G en een uitgang X. Ingang A kan beschreven worden in vijf termen, waaronder 'm' en 'n'. Ingang G kan beschreven worden in vijf termen, waaronder 'h'. Uitgang X kan beschreven worden in vijf termen, waaronder 'e' en 'o'. Het te sturen proces kan volledig beschreven worden met twee vage regels:
Regel 1:
ALS A IS m EN G IS h DAN X is e
Regel 2:
ALS A IS n EN G IS h DAN X IS o
Op het moment dat de fuzzy-processor de regels uitwerkt is de actuele waarde van de ingangsgrootheden:
A = 175
G = 190
Het volledige proces van inferentie is samengevat in de onderstaande figuur. De bovenste grafiek geeft de inferentie van de eerste regel. Natuurlijk zijn de LF's 'm' van A en 'h' van G actief, want die staan vermeld in de eerste regel. Uit de actuele waarden 175 en 190 kunnen de twee corresponderende μ-waarden berekend worden, waaruit blijkt dat μA = 0,25 en μG = 1.
Omdat beide variabelen door middel van een EN-operator gekoppeld zijn, telt alleen de laagste μ-waarde, in dit geval 0,25. Deze wordt horizontaal doorgetrokken naar de grafiek van de uitgang X. Hier is de LF van 'e' actief. Er ontstaat nu een nieuwe vage verzameling, die begrensd wordt door de μ-waarde 0,25. Deze fuzzy-functie is gearceerd weergegeven.
 |
| Het principe van inferentie toegelicht aan de hand van een voorbeeld. (© 2021 Jos Verstraten) |
De onderste grafiek geeft de inferentie van de tweede regel. Nu is de LF An actief, alsmede de LF van Gh. De waarden van de ingangen zijn natuurlijk nog niet gewijzigd, met als gevolg dat u nu twee μ-waarden van 0,75 en 1 kunt berekenen. Ook nu wordt er gekoppeld met een EN-operator, zodat de laagste μ (0,75) weer wordt doorgetrokken naar de uitgangsgrafiek. Hier is de LF van Xo actief. Ook nu berekent het inferentie-proces een nieuwe vage verzameling, die nu begrensd wordt door de μ-waarde 0,75.
Soorten inferentie
Er zijn verschillende algoritmen ontwikkeld voor het opstellen van fuzzy-functies door middel van inferentie. De meest toegepaste zijn:
- MIN-MAX inferentie
- MAX-PROD inferentie
De verschillen worden toegelicht aan de hand van de onderstaande figuur.
 |
| Twee vormen van inferentie-strategie: links MIN-MAX, rechts MAX-PROD. (© 2021 Jos Verstraten) |
MIN-MAX inferentie
De linker grafiek geeft het resultaat van een MIN-MAX inferentie. De actieve LF van de uitgang wordt begrensd door de actieve waarde van de μ van de ingangen.
MAX-PROD inferentie
De rechter grafiek toont wat er gebeurt als wordt gewerkt volgens het MAX-PROD schema. Nu wordt de actieve LF van de uitgang niet begrensd, maar verkleind in hoogte, tot de top samenvalt met de actieve waarde van μ.

Inferentie-strategieën
Er is geen sprake van een goede inferentie-strategie. Voor sommige toepassingen kunt u het best gebruik maken van de MIN-MAX algoritmen, andere toepassingen geven de beste resultaten als u volgens MAX-PROD werkt. Bovendien zijn er tientallen andere inferentie-strategieën theoretisch uitgewerkt.
De compositie
Door de inferentie wordt iedere regel van het redeneermechanisme omgezet in een fuzzy-functie, die het door de uitgang te volgen gedrag definieert bij bepaalde waarden van de ingangsvariabelen. Natuurlijk hebt u daar in de praktijk vrij weinig aan, want wat moet ontstaan is een eenduidige uitgangsfunctie, waaruit een welbepaalde waarde voor de uitgang kan worden afgeleid. Op de een of andere manier moeten alle afzonderlijke fuzzy-functies van de uitgang worden gecombineerd tot één algemeen geldende functie, die rekening houdt met alle stellingen die in alle regels vastgelegd zijn. Dit proces noemt men de 'compositie'.
In de meeste gevallen gaat dit door de afzonderlijke fuzzy-functies met elkaar te verknopen met een 0R-operator. Dat is vrij logisch, want u kunt er van uitgaan dat het systeem aan alle regels van het redeneermechanisme moet voldoen, hetgeen te vertalen is naar een OR-functie.
In het eerder in dit artikel besproken voorbeeld levert de compositie dus een eenduidige uitgangsfunctie op, die ontstaat door de twee deelfuncties te OR-ren. Hetgeen, zoals reeds beschreven, er op neer komt dat de oppervlakken van de deelfuncties tot één oppervlak worden verenigd. Een en ander wordt grafisch toegelicht in de onderstaande figuur.
 |
| Ontstaat van de uiteindelijke uitgangsfunctie van het fuzzy-proces. (© 2021 Jos Verstraten) |
De defuzzificatie
Inleiding
De uitgangsfunctie die door de compositie ontstaat bepaalt volledig de reactie van de uitgang op de momentele ingangswaarden. Natuurlijk moet u uit deze functie een expliciete waarde van de uitgangsvariabele afleiden. Dit proces noemt men de 'defuzzificatie'. Ook hiervoor zijn verschillende strategieën ontwikkeld, waarvan de voornaamste zijn:
- de center of gravity strategie COG
- de maximum strategie MAX
- de mean of maximum strategie MOM
De center of gravity strategie wordt het vaakst toegepast.
De center of gravity strategie COG
Bij deze strategie bepaalt de fuzzy-processor het zwaartepunt S van de uitgangsfunctie. Het zwaartepunt of 'centroide' is een wiskundig begrip, dat soms met eenvoudige en soms met ingewikkelde wiskunde op ieder plat vlak kan worden toegepast. In de onderstaande figuur is getekend waar het zwaartepunt van de uitgangsfunctie van het besproken voorbeeld ligt. Door uit dit zwaartepunt S een verticaal hulplijntje te tekenen naar de horizontale as kunt u de numerieke waarde van de uitgangsvariabele aflezen. In het voorbeeld betekent dit dat het fuzzy systeem de uitgangsvariabele X een waarde van 80 geeft, als de ingangsvariabele A gelijk is aan 175 en de ingangsvariabele G gelijk is aan 190.
Nadelen van de COG-strategie
De COG-strategie heeft een groot nadeel, dat toegelicht wordt aan de hand van onderstaande figuur. In die tekening zijn twee uitgangsfuncties getekend, die duidelijk een andere vorm hebben. Als u van beide functies het zwaartepunt berekent en daarvan de horizontale waarde uitzet op de horizontale as blijkt dat deze waarden gelijk zijn! In beide gevallen zou de uitgangsvariabele dus dezelfde numerieke waarde krijgen, terwijl het duidelijk is dat de ingangsvariabelen niet gelijk zijn!
Een tweede nadeel van de COG-strategie is dat het bepalen van het zwaartepunt bij ingewikkelde, niet-lineaire uitgangsfunctie een hele klus is, waar zelfs een snelle processor de nodige tijd over doet.
De MAX-strategie
Bij de MAX-strategie wordt het punt van de uitgangsfunctie bepaald dat de hoogste waarde op de μ-as heeft. Vanuit dit punt M wordt weer een verticale lijn naar de horizontale as getrokken, waar de numerieke waarde van de uitgangsvariabele afgelezen kan worden. In de onderstaande figuur is dit toegelicht aan de hand van een voorbeeldje. Voordeel van de MAX-strategie is dat het bepalen van het maximum van een curve wiskundig heel snel gaat en dat de processor dus weinig rekentijd nodig heeft voor de de-fuzzificatie.
De COG-strategie heeft een groot nadeel, dat toegelicht wordt aan de hand van onderstaande figuur. In die tekening zijn twee uitgangsfuncties getekend, die duidelijk een andere vorm hebben. Als u van beide functies het zwaartepunt berekent en daarvan de horizontale waarde uitzet op de horizontale as blijkt dat deze waarden gelijk zijn! In beide gevallen zou de uitgangsvariabele dus dezelfde numerieke waarde krijgen, terwijl het duidelijk is dat de ingangsvariabelen niet gelijk zijn!
Een tweede nadeel van de COG-strategie is dat het bepalen van het zwaartepunt bij ingewikkelde, niet-lineaire uitgangsfunctie een hele klus is, waar zelfs een snelle processor de nodige tijd over doet.
 |
| Twee verschillende uitgangsfuncties leveren dezelfde numerieke waarde voor de uitgang. (© 2021 Jos Verstraten) |
De MAX-strategie
Bij de MAX-strategie wordt het punt van de uitgangsfunctie bepaald dat de hoogste waarde op de μ-as heeft. Vanuit dit punt M wordt weer een verticale lijn naar de horizontale as getrokken, waar de numerieke waarde van de uitgangsvariabele afgelezen kan worden. In de onderstaande figuur is dit toegelicht aan de hand van een voorbeeldje. Voordeel van de MAX-strategie is dat het bepalen van het maximum van een curve wiskundig heel snel gaat en dat de processor dus weinig rekentijd nodig heeft voor de de-fuzzificatie.
 |
| Defuzzificatie volgens de MAX-strategie. (© 2021 Jos Verstraten) |
De MOM-strategie
De MOM-defuzzificatie werkt volgens een heel eigen principe. Er wordt namelijk géén compositie toegepast. Iedere regel uit het redeneermechanisme wekt, zoals bekend, een specifieke functie op voor de uitgang. Bij de MOM-strategie wordt van iedere uitgangsfunctie het maximum bepaald en de bijbehorende μmax berekend. Nadien wordt het gemiddelde van al deze waarde berekend en dit getal wordt gebruikt om de reële waarde van de uitgangsvariabele te bepalen.
Het voordeel van deze strategie is dat de fuzzy-processor veel minder hoeft te rekenen en daardoor veel sneller kan werken.
Samenvatting van het fuzzy logic procédé
Hiermee is het gehele fuzzy-proces stap na stap besproken. Een samenvatting lijkt op zijn plaats. Het oplossen van een regelprobleem door middel van vage logica gaat als volgt:
- Stap 1
Bepaal wat de in- en de uitgangsvariabelen zijn. - Stap 2
Bepaal de minimum en maximum grenzen van deze variabelen. - Stap 3
- Onderzoek hoeveel termen er nodig zijn om het gedrag van de variabelen te beschrijven.
- Stap 4
Stel de lidmaatschapsfuncties voor alle termen op. - Stap 5
Onderzoek hoe de uitgangsvariabele zich moet gedragen in functie van de ingangsvariabelen. - Stap 6
Stel aan de hand hiervan de regels van het redeneermechanisme op. - Stap 7
Bepaal welke inferentie u het best kunt toepassen. - Stap 8
Bepaal welke defuzzificatie strategie het best kan worden toegepast.
Experimenteren met fuzzy logic
Door het 'Department of Mathematical Analysis and Applications of Mathematics' van de Tsjechische universiteit 'Palacký University Olomouc' is het programma 'FuzzME' ontwikkeld. Dit letterwoord staat voor 'Fuzzy Models of Multiple-Criteria Evaluation'. Met dit programma kunt u experimenteren met fuzzy logic.
De demoversie kunt u downloaden van Demo-versie van FuzzME en is vijf dagen bruikbaar.