Terug naar de basis: de audio-CD speler
44.100 • 2 • 16 bit omzetten naar analoge signalen
In principe lijkt de taak van de analoge elektronica in een audio-CD speler het toppunt van eenvoud als u deze vergelijkt met de ingewikkelde functies van de digitale elektronica. Zet de 44.100 • 2 • 16 bit brede digitale codes die per seconde het digitale deel verlaten om in mooie analoge spanningen. Niets lijkt simpeler dan dat. Bouw twee zestien bit brede DAC's in, sluit het getrapte uitgangssignaal van deze schakelingen af met laagdoorlaat filtertjes om het trapvormige verloop van de uitgangsspanningen af te vlakken en dat is dat.
Zo simpel is het echter niet! Het is nu net in dat analoge deel dat de grote verschillen zitten tussen een CD-speler van het type A van merk B en een CD-speler van het type X van merk Y. Specialisten beweren zelfs dat zij in staat zijn alleen aan de klankkleur van het door een CD-speler geproduceerde geluid merk en type te kunnen achterhalen!
Analoge imperfecties spelen een rol
Bij het omzetten van de digitale codes in analoge spanningen worden de ontwerpers geconfronteerd met alle in de analoge elektronica ingebouwde imperfecties, zoals signaalvervormingen, looptijdverschillen, opslingeringen en faseverschuivingen. Dat zijn grootheden waarvan de ideale waarde, namelijk nul, in de praktijk alleen benaderd kan worden. Maar dat zijn dus ook grootheden waarvan deze ideale waarde steeds opnieuw door kleine verbeteringen van bestaande schakelingen beter benaderd kan worden.
Aan systemen geen gebrek
Een en ander heeft ertoe geleid dat er tientallen verschillende systemen worden toegepast om de digitale audiocodes om te zetten in analoge spanningen. Steeds opnieuw verzinnen fabrikanten van CD-spelers nieuwe systemen en schakelingen die nog minder vervormen en nog transparanter geluid produceren dan alles wat al op de markt is. Een kort, maar onvolledig overzicht van de DAC-systemen die worden toegepast:
- 14 bit switched real sampling.
- 14 bit real sampling.
- 16 bit switched real sampling.
- 16 bit real sampling.
- 16 bit cascaded real sampling.
- 14 bit dual upsampling.
- 16 bit dual upsampling.
- 14 bit quadruple upsampling.
- 16 bit quadruple upsampling.
- Adaptive floating decimal upsampling.
- Pulse width modulation convertion.
- 1 bit switched capacitor convertion.
U merkt dat het begrip 'upsampling' hier vaak in voorkomt. Het heeft echter geen zin dit begrip te bespreken zonder eerst diep in te gaan op de fundamentele tekortkomingen van de traditionele digitaal naar analoog omzetting bij audio.
De traditionele DAC
In de onderstaande figuur is het basisprincipe van een traditionele drie bit brede DAC getekend. De schakeling bestaat uit drie stroombronnen, die zeer constante stromen genereren die een zeer nauwkeurige onderlinge verhouding hebben van 1/2/4. Deze stromen vloeien via elektronische schakelaars MSB tot en met LSB naar de ingang van een stroom naar spanning omzetter. Deze schakeling is op de bekende manier samengesteld uit een operationele versterker met een terugkoppel weerstand RF. De schakelaars worden bediend door de drie bits van de digitale ingangscode. Als een bit 'H' is sluit de schakelaar. Als de code 'L-L-L' (van MSB naar LSB) is zullen alle schakelaars open staan en vloeit er geen stroom naar de ingang van de op-amp. De uitgangsspanning is nul. Als de code wordt verhoogd tot 'L-L-H' zal de LSB-schakelaar sluiten. Er vloeit nu een stroom I naar de ingang van de op-amp. Deze stroom wordt omgezet in een spanning ΔU. Als de digitale code wordt opgehoogd tot 'L-H-L' zal de tweede schakelaar sluiten en de eerste weer openen. Er vloeit nu een stroom 2•I naar de op-amp, het gevolg is dat op de uitgang een spanning ontstaat van 2•ΔU.
U kunt dus besluiten dat als u de code op de digitale ingangen stapsgewijs verhoogt van 'L-L-L' naar 'H-H-H' er op de uitgang van de DAC een trapvormig verlopende spanning ontstaat, waarvan iedere stap ΔU groter is dan de vorige. Dit verband tussen digitale ingangscode en analoge uitgangsspanning is in de bovenstaande figuur rechts getekend.
 |
| Het principe van een drie bit brede DAC. (© 2019 Jos Verstraten) |
De besproken schakeling werkt uitstekend voor resoluties tot 10 bit en bij lage snelheden. Het CD-systeem werkt echter met niet minder dan zestien bit en bovendien met een tamelijk hoge snelheid. De traditionele DAC laat het onder deze omstandigheden volledig afweten.
Er zijn twee problemen, namelijk:
- De nauwkeurigheid van de stroomverhouding van de stroombronnen.
- De schakelsnelheid van de stroombronnen en elektronische schakelaars.
Deze twee problemen worden in de volgende paragraafjes besproken.
De nauwkeurigheid van de stroomverhouding
Zoals geschreven ontstaat op de uitgang van een DAC een trapvormige spanning als aan de ingang alle mogelijke codecombinaties van het digitale woord in de logische volgorde worden doorlopen. Het zal duidelijk zijn dat iedere trap alleen precies ΔU groter is dan de vorige als de onderlinge verhouding van de stromen die de stroombronnen genereren klopt. Als een van de stroombronnen een te grote tolerantie heeft, dan ontstaat een verschijnsel dat men 'niet-monotonie' noemt. Dit wordt toegelicht aan de hand van de onderstaande figuur. Bij bepaalde codewisselingen zal de analoge uitgangsspanning niet met de verwachte waarde ΔU toenemen, maar met een grotere of kleinere waarde. In extreme gevallen kan dit er zelfs toe leiden dat de reële uitgangsspanning in een gebied komt te liggen dat in feite voorbehouden is aan een andere digitale code op de ingangen. In dat geval is sprake van niet-monotoon gedrag van de DAC.
Uiteraard zal dit niet alleen bij slechts één bepaalde trap gebeuren (tenzij de stroomafwijking uitsluitend in de stroombron van de MSB-schakelaar zit), maar zich regelmatig herhalen. Niet-monotone trappen ontstaan telkens de stroombron met de grote tolerantie in- of uitschakelt. Dit niet-monotone verschijnsel veroorzaakt een grote vervorming op het analoge uitgangssignaal.
 |
| Het verschijnsel 'niet-monotonie' grafisch toegelicht. (© 2019 Jos Verstraten) |
Dit noemt men de 'beter dan één LSB nauwkeurigheidseis van het MSB'. Is deze nauwkeurigheid kleiner, dan werkt de DAC in ieder geval niet-monotoon en zal de stroom van het LSB volledig verdrinken in de onnauwkeurigheid van de stroom van het MSB. Er zal dan bij bepaalde codes geen enkel verband bestaan tussen de logische waarde van dit LSB bit en de waarde van het analoge signaal.
Ook voor de MSB-1 en MSB-2 bits gelden zeer hoge nauwkeurigheidseisen. Het zal duidelijk zijn dat het fabriceren van een stroombron met een tolerantie van 0,003 % onmogelijk is, zeker als men deze tolerantie ook over een tamelijk groot temperatuurbereik moet handhaven en de schakeling bovendien niet te duur mag worden vanwege de inbouw in een massaproduct als een CD-speler.
De schakelsnelheid van de stroombronnen
Bij het CD-systeem leveren de digitale schakelingen 44.100 keer per seconde 2 • 16 bit brede woorden aan de ingangen van de digitaal naar analoog omzetter. De DAC moeten dus tamelijk snel werken. Nu duurt het uiteraard een bepaalde tijd, de conversietijd genoemd, alvorens alle elektronische schakelaars in de DAC zich hebben gesloten of geopend en alvorens de actieve stroombronnen zich hebben gestabiliseerd. Gedurende deze conversietijd zal de uitgangsspanning van de DAC onvoorspelbaar zijn. In de praktijk ontstaan tijdens de codewisseling zogenoemde 'spikes' of 'glitches' op de analoge uitgangsspanning, korte piekspanningen met ongedefinieerde grootte en polariteit. Dit verschijnsel wordt grafisch toegelicht aan de hand van de onderstaande figuur.
De grootte van deze spikes is afhankelijk van hoeveel bits er omschakelen. Hoe meer bits omschakelen, hoe meer elektronische schakelaars van de ene naar de andere toestand moeten omschakelen en hoe onvoorspelbaarder het gedrag van de schakeling wordt. Deze spikes veroorzaken een niet onaanzienlijke vervorming van het analoge uitgangssignaal van de CD-speler. Dit verschijnsel is een van de redenen waarom het absoluut noodzakelijk is filters na de DAC op te nemen. Een van de taken van dit filter is het verzwakken van deze spikes die voornamelijk uit hogere harmonischen bestaan en dus hoorbaar zijn als ruis.
 |
| Het ontstaan van 'spikes' bij het overschakelen van de ene digitale code naar de andere. (© 2019 Jos Verstraten) |
Theoretische problemen van het DAC-principe
Inleiding
Zelfs als men er in zou slagen een ideale DAC te ontwerpen, dan nog zouden er grote problemen op te lossen zijn bij het reconstrueren van een onvervormd audiosignaal uit de zestien bit brede audiocodes van de CD. Deze problemen hebben te maken met de theoretische principes die ten grondslag liggen aan het gecombineerde ADC-DAC procédé. Er zijn drie factoren te noemen:
- De digitale cross-over vervorming.
- De quantiseringsbandbreedte.
- De quantiseringsruis.
Deze drie factoren worden in de volgende drie paragrafen besproken.

De digitale cross-over vervorming
In principe wekt een digitaal naar analoog omzetter een unipolair uitgangssignaal op. Als de digitale ingangscode gelijk is aan 'L-L-........-L-L' zal de uitgangsspanning 0 V bedragen. Is de digitale code gelijk aan 'H-H-........-H-H' dan zal de analoge uitgangsspanning gelijk zijn aan een bepaalde maximale positieve waarde. De audiosignalen die door het CD-systeem verwerkt worden zijn echter bipolair. Het geluidssignaal zal zowel positief als negatief zijn. Dat heeft tot gevolg dat het volledige bereik van de ADC bij de opname moet opgesplitst worden in een positief deel en een even groot negatief deel. De nuldoorgang komt dan overeen met een code-overgang van 'L-H-H-........-H-H' naar 'H-L-........-L-L'. Deze laatste digitale code kunt u de 'digitale massa' van het systeem noemen. U kunt ook stellen dat de waarde van het MSB bit de polariteit van het analoge signaal bepaalt. Is dit negatief, dan is het MSB 'L', is het signaal positief dan is het MSB 'H'.
Bij de reconstructie van het analoge signaal uit de digitale code in de CD-speler zal dezelfde situatie ontstaan. Bij zeer kleine sinusoidaal verlopende analoge spanningen zullen alle bits van de code voortdurend gezamenlijk moeten omschakelen en wel op het moment dat het analoge signaal van polariteit wisselt. Juist op dat zeer kritische moment in het audiosignaal is de kans op glitches dus het grootst. Bovendien zal bij het omschakelen rond de analoge nul nu net het MSB, waarvan de convertorstroom het allernauwkeurigst moet zijn, een overheersende rol spelen. Zelfs de geringste afwijking in de stroomverhouding (en dus in de spanningsverhouding aan de uitgang van de DAC) heeft tot gevolg dat er ongewenste pieken op de analoge uitgangsspanning verschijnen.
In de onderstaande figuur figuur wordt dit toegelicht aan de hand van een praktijksituatie. De foto toont de analoge uitgangsspanning van een zestien bit DAC die met codes wordt gestuurd die overeen komen met een zeer kleine sinusspanning. De vervorming die rond de nuldoorgang van het signaal ontstaat is enigszins te vergelijken met de vervorming die de allereerste generatie transistorversterkers ontsierde. Deze vervorming noemde men de 'cross-over'. Vanwege de analogie (niet in ontstaan, maar in hoorbaar effect) wordt dit verschijnsel bij het CD-systeem de 'digitale cross-over' vervorming genoemd.
 |
| Digitale cross-over vervorming bij het omschakelen van het MSB. (© 2019 Jos Verstraten) |
Als u een zuiver sinusoidaal verlopende analoge spanning digitaliseert en de digitale codes vervolgens weer omzet in een analoog signaal dan zal er, zie de onderstaande figuur, zelfs bij het beste systeem steeds een groot verschil bestaan tussen de ingangs- en de uitgangsspanning. Het uitgangssignaal verloopt trapvormig en is dus geen zuivere sinus.
 |
| Fundamentele eigenschap van ieder ADC-DAC systeem is dat de teruggewonnen uitgangsspanning trapvormig verloopt. (© 2019 Jos Verstraten) |
In theorie ontstaan dan een oneindig aantal harmonische groepen rond de veelvouden van de samplefrequentie, ieder voorzien van 20 kHz brede symmetrische zijbanden. Bij het CD-systeem bedraagt de samplefrequentie 44,1 kHz. De eerste harmonische groep ligt dus rond deze waarde (ft in de tekening). Maar 44,1 kHz - 20 kHz is echter 24,1 kHz! De laagste harmonische van de linker zijband van deze eerste groep ligt dus slechts 4,1 kHz boven 20 kHz bandbreedte van het CD-systeem!
Het zal duidelijk zijn dat u al deze harmonischen uit het uitgangssignaal van de DAC moet filteren. Weliswaar zijn deze frequenties niet hoorbaar, maar zij kunnen in de op de CD-speler aangesloten eindversterker voor grote problemen zorgen. Zou deze versterker immers last hebben van intermodulatievervorming, dan zouden allerlei som- en verschilfrequenties ontstaan die wel degelijk binnen de hoorbare band vallen. Het geluid zou ernstig vervormd klinken.
 |
| Frequentiespectrum van een gedigitaliseerd en nadien herwonnen audiosignaal met een bandbreedte van 20 kHz. (© 2019 Jos Verstraten) |
Vandaar dat de eis gesteld wordt dat alle harmonischen die in het uitgangssignaal van de DAC zitten en frequenties hebben boven de 20 kHz minstens met 50 dB verzwakt moeten worden. Op zich zijn er talrijke analoge filterschakelingen te verzinnen die signalen boven 20 kHz met het genoemde aantal dB kunnen verzwakken. Het probleem ontstaat echter door het feit dat het eerste met 50 dB te verzwakken signaal een frequentie heeft van 24,1 kHz. Er moeten dus zeer steile filters toegepast worden. Meestal gebruikt men een Chebyshew-filter van de negende of zelfs de elfde orde. Zoals uit de karakteristiek van de onderstaande figuur blijkt heeft zo'n filter een uitstekende amplitudegrafiek. De fasekarakteristiek is echter waardeloos. Door groeptijdverschillen in de audioband tot 20 kHz zullen er opslingeringen ontstaan als het audiosignaal pulsvormig verloopt. Deze opslingeringen zijn erg goed te horen en veroorzaken een typische vervorming, zie het oscillogram links op de laatste illustratie van deze pagina.
 |
| Amplitudekarakteristiek van een elfde orde laagdoorlaat filter. (© 2019 Jos Verstraten) |
De kwantiseringsruis is een rechtstreeks gevolg van het stapvormige verloop van de uitgangsspanning van een DAC. Als u de in- en de uitgangsspanning van het standaard systeem van elkaar aftrekt dan ontstaat er een verschilsignaal dat er uitziet zoals getekend in de onderste grafiek van de onderstaande figuur.
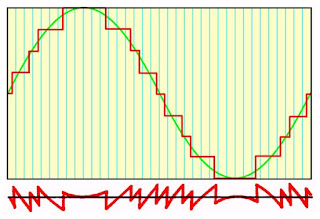 |
| Het ontstaan van de kwantiseringsruis (onder). (© 2019 Jos Verstraten) |
Men kan de theoretische waarde van deze kwantiseringsruis berekenen. Voor een zestien bit systeem ligt deze ruis 96 dB onder het maximale signaal. Vandaar dat steeds gesteld wordt dat het CD-systeem een signaal/ruis-verhouding van 96 dB heeft. De ruis neemt toe met 6 dB per bit naarmate de DAC minder bits van de audiocode verwerkt. Een veertien bit systeem heeft dus een maximale signaal/ruis-verhouding van 84 dB. Het zal duidelijk zijn dat de basisfrequentie van de kwantiseringsruis gelijk is aan de bemonsteringssnelheid van het systeem. Bij het CD-systeem ligt deze basisfrequentie dus bij 44,1 kHz.
Het principe van upsampling
Inleiding
Van de twaalf in het vorige subkopje opgesomde DAC-systemen zijn er niet minder dan vijf waarin het woord 'upsampling' voorkomt. Upsampling moet dus wel een belangrijk principe zijn in de CD-technologie. Dat is het ook, want een heleboel CD-spelers werken met dit principe. Opgemerkt moet worden dat vaak gebruik wordt gemaakt van de term 'oversampling'.
Verhogen van de samplingfrequentie
Als de beschreven problemen op een rijtje worden gezet blijkt dat de lage samplingfrequentie van 44,1 kHz de meeste problemen veroorzaakt. Als deze frequentie verdubbeld zou kunnen worden tot 88,2 kHz zou het vermogen van de kwantiseringsruis over een groter frequentiegebied verspreid worden waardoor er minder energie in de 0 Hz tot 20 kHz band zou overblijven. Bovendien zou de kwantiseringsbandbreedte er heel anders komen uit te zien.

Overbemonstering of upsampling
Nu werkt het audio-CD systeem per definitie met een bemonsteringsfrequentie van slechts 44,1 kHz en daar valt niets aan te veranderen. Zou men willen overschakelen naar de dubbele frequentie, dan moeten in de CD-speler extra monsters kunstmatig worden tussengevoegd tussen de 44.100 zestien bit brede monsters die de digitale schakeling per seconde aflevert. Dat proces noemt men in het algemeen 'upsampling' of in het Nederlands 'overbemonstering'.
Het zal wel duidelijk zijn dat met 'dual upsampling' het proces wordt aangegeven waarbij de samplingfrequentie wordt verhoogd van 44,1 tot 88,2 kHz. Dat lijkt een onmogelijke opgave, maar zoals zo vaak blijkt ook nu weer dat digitaal alles kan. Men is er in geslaagd digitale schakelingen te ontwerpen, de zogenaamde 'digitale transversaal filters', die dat kunststukje voor elkaar brengen.
Maar er is meer! Toen men toch eenmaal bezig was met het ontwerpen van dat soort schakelingen kwam men tot de ontdekking dat het net zo eenvoudig mogelijk was de samplingfrequentie te verviervoudigen. De samplingfrequentie van de DAC wordt dan 176,4 kHz en er moeten drie monsters tussen iedere twee monsters die de digitale schakeling levert worden tussengevoegd. Dit systeem noemt met 'quadruple upsampling'.
De effecten van upsampling op de kwantiseringsbandbreedte
Het effect van dual of quadruple upsampling op de bandbreedte van het herwonnen signaal kan het best grafisch verklaard worden. De kwantiseringsbandbreedte van een met een bemonsteringssnelheid van 88,2 kHz herwonnen signaal is getekend in de onderstaande figuur.
De eerste bundel harmonischen ligt nu rond de 88,2 kHz zodat de laagste harmonische een frequentie heeft van 68,2 kHz. Er zit dus nu een frequentieverschil van 48,2 kHz tussen de maximale frequentie van het signaal en deze eerste te verwijderen harmonische. Het gevolg is dat de analoge filterschakeling van een heel wat lagere orde kan zijn en de fasekarakteristiek van zo'n filter is heel wat beter te manipuleren dan deze van een elfde orde filter.
 |
| De kwantiseringsbandbreedte bij een samplingfrequentie van 88,2 kHz. (© 2019 Jos Verstraten) |
Het voordeel van quadruple upsamplen volgt uit het frequentiespectrum van zo'n signaal. Dat is getekend in de onderstaande figuur. Het zal duidelijk zijn dat er nu helemaal geen problemen meer bestaan bij het ontwerpen van het analoge filter. De afstand tussen 20 kHz en de eerste harmonische is nu zo groot dat zelfs het meest eenvoudige derde orde actieve Besselfilter goed genoeg is.
 |
| De kwantiseringsbandbreedte bij quadruple upsamplen. (© 2019 Jos Verstraten) |
Om dat toe te lichten is in de onderstaande figuur het praktisch schema van het analoge filter getekend, dat door Philips werd ontwikkeld voor gebruik in zijn viervoudig overbemonsterde CD-spelers.
 |
| Het analoge derde orde Besselfilter dat achter een viervoudig overbemonsterde DAC geschakeld kan worden. (© 2019 Jos Verstraten) |
Een tweede voordeel van het verhogen van de samplefrequentie van de DAC is dat de kwantiseringsruis over een groter frequentiegebied wordt verspreid en het aandeel in de 20 Hz tot 20 kHz band lager wordt. Een en ander wordt grafisch toegelicht aan de hand van de vergelijking in de onderstaande figuur figuur. Links is het reeds bekende plaatje getekend van de grootte van de kwantiseringsruis bij normale sampling. Als men echter gaat upsamplen zal één periode van het oorspronkelijke signaal vaker worden omgezet in een analoge trapspanning. In de veronderstelling dat de kunstmatig tussengevoegde monsters goed berekend zijn zal de trapspanning de vorm van het originele audiosignaal bovendien beter benaderen. Beide gegevens hebben tot resultaat dat de kwantiseringsruis kleiner is en bovendien een hogere basisfrequentie heeft, zie de rechter figuur. Het hoorbare gevolg is dat er veel minder ruisvermogen in de band tussen 20 Hz en 20 kHz gaat zitten en de vervorming van het signaal kleiner wordt.
 |
| Vergelijking van de kwantiseringsruis bij normale sampling en upsampling. (© 2019 Jos Verstraten) |
De werking van een digitaal transversaal filter
Niet zo gemakkelijk als het lijkt
Het lijkt logisch te veronderstellen dat bij dual upsampling het digitaal transversaal filter de waarde van sample n en sample n+1 bepaalt, de gemiddelde waarde berekent, deze gemiddelde waarde weer omzet in een zestien bit brede digitale code en dit nieuwe kunstmatig gegenereerde sample tussen de samples n en n+1 voegt. Voor een quadruple systeem zou het filter dan drie tussensamples moeten berekenen.
Niets is echter minder waar! De werking van een digitaal transversaal filter (DTF) is erg moeilijk te doorgronden zonder diepgaande kennis van fundamentele theoretisch/wiskundige elektronica en met name van de tijd- en frequentie-domein theorieën.
Laat ons toch een poging wagen! Een digitaal transversaal filter heeft, wel beschouwd, hetzelfde effect op het uiteindelijke analoge signaal als een analoog laagdoorlaat filter. De ruis wordt verminderd en door de werking van het DTF kan het analoog filter veel minder verzwakken. Het lijkt dus net alsof het DTF als eerste en voornaamste laagdoorlaat filter kan opgevat worden en dat de werking ervan alleen nog iets moet aangevuld worden door het tweede analoog filter.
Als een DTF als laagdoorlaat filter werkt, dan moet het ook aan dezelfde wetten gehoorzamen als een traditioneel analoog filter. De digitale schakelingen leveren zestien bit brede woorden, de digitale representanten van analoge spanningen. Vanwege het discontinue karakter van de code (deze verandert immers 44.100 keer per seconde plotseling van waarde) kunt u de ingangsspanning van het DTF voorstellen als een opeenvolging van smalle, steile pulsjes.
De pulsweergave van filters
De volgende vraag die beantwoord moet worden is hoe een analoog laagdoorlaat filter reageert als u op de ingang een smalle, steile puls aanlegt. De pulsweergave van een analoog laagdoorlaat filter is getekend in de onderstaande figuur. Er bestaat een ondubbelzinnig verband tussen het amplitudeverloop aan de uitgang, de amplitude van de ingangspuls en het tijdsverloop. Het amplitudeverloop kan volledig wiskundig worden uitgedrukt. Voor ieder punt op de tijd-as kan dus een constante factor of coëfficiënt k worden berekend die, vermenigvuldigd met de amplitude van de ingangspuls, de amplitude van de uitgangsspanning geeft voor het specifieke punt op de tijd-as. Het verloop van de uitgangsspanning kan dus worden gedefinieerd door het berekenen van een aantal coëfficiënten k(tn), die ieder de amplitude van het uitgangssignaal definiëren op het tijdstip tn. Hoe meer coëfficiënten u berekent, hoe nauwkeuriger u de uitgangsspanning van het analoge filter kunt reconstrueren.
 |
| De reactie van een laagdoorlaat filter op een smalle puls op de ingang. (© 2019 Jos Verstraten) |
Het zal duidelijk zijn dat het digitaal transversaal filter op een en hetzelfde moment toegang moet hebben tot opeenvolgende samples, wil de berekening coëfficiënten maal amplitude van de samples uitgevoerd kunnen worden.
Het blokschema van een digitaal transversaal filter
Vandaar dat een digitaal transversaal filter steeds is opgebouwd volgens het blokschema van de onderstaande figuur. De zestien bit brede digitale monsters die van de digitale elektronica komen worden ingelezen in een schuifregister. Dat schuifregister kan opgevat worden als de tijd-as uit de vorige figuur.
Een digitaal monster dat op een bepaald tijdstip wordt ingelezen zal immers enige tijd later doorgeschoven zijn naar het midden van het register. Het schuifregister heeft aftakkingen die naar binaire vermenigvuldigers gaan. In deze trappen wordt de waarde van de monsters vermenigvuldigd met de reeds genoemde coëfficiënten. Terwijl een sample door het register schuift wordt na iedere verplaatsing de waarde van het monster met een nieuwe coëfficiënt vermenigvuldigd. Op deze manier wordt de respons van een analoog filter nagebootst.
Al deze berekende nieuwe waarden gaan naar een soort van mengschakeling. Daar wordt het effect van de overlapping ingecalculeerd en wordt de nieuwe monsterstroom samengesteld. Bij een systeem dat werkt met 14 bit brede DAC's zal de nieuwe monsterstroom bestaan uit veertien bit brede monsters, die met de dubbele of de vierdubbele frequentie worden uitgevoerd.
 |
| De principiële samenstelling van een digitaal transversaal filter. (© 2019 Jos Verstraten) |
Een DTF is dus een echt laagdoorlaat filter. Als dusdanig heeft een dergelijke schakeling dan ook een amplitude/frequentie-karakteristiek. In de onderstaande figuur wordt deze karakteristiek gegeven voor het DTF van het type SAA7220 dat door Philips werd ontwikkeld. Deze karakteristiek is zo goed als ideaal. De kleine rimpel in de doorlaatband wordt veroorzaakt door afrondingsfouten in de waarde van de toegepaste filtercoëfficiënten. De nauwkeurigheid van het filter hangt af van de lengte van het interne schuifregister. Hoe langer dit is, hoe langer een digitaal monster in het filter blijft en hoe meer amplitudecoëfficiënten berekend kunnen worden.
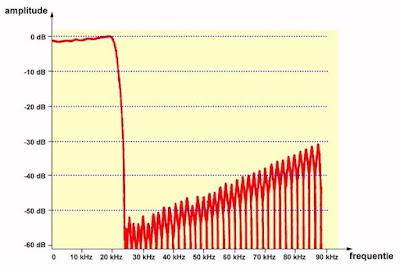 |
| De amplitude/frequentie-karakteristiek van het digitaal transversaal filter SAA7220 van Philips. (© 2019 Jos Verstraten) |
 |
| Vergelijking van de pulsweergave van een elfde orde analoog filter en een digitaal transversaal filter. (© Elrad-lab) |
Mustool MDS8207 scope + multimeter


