|
Pulsvormige signalen gebruikt u, naast sinusvormige signalen, het meest in de dagelijkse praktijk. U kunt er uiteraard digitale schakelingen mee aansturen. Een puls kunt u echter ook gebruiken voor het snel beoordelen van de weergavekarakteristieken van analoge en digitale schakelingen. |
Achtergrondinformatie
Wat is een pulsvormige spanning?
Een puls is een elektrische spanning die maar twee waarden kan aannemen en die minstens twee keer snel heen en weer schakelt tussen deze twee waarden. In de onderstaande figuur hebben wij de ideale vorm van een aantal pulsvormige signalen weergegeven. Een 'burst' is de opeenvolging van een aantal identieke pulsen.
 |
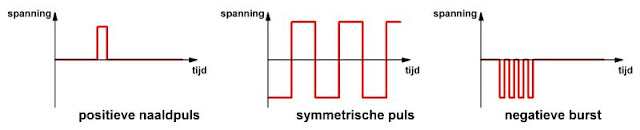| Voorstelling van een paar ideale pulsvormige signalen. (© 2019 Jos Verstraten) |
Uiteraard zullen de geschetste ideale pulsvormen in de praktijk niet voorkomen. Als u een puls gedetailleerd onderzoekt, stelt u vast dat zo'n signaal een heleboel onderdelen bevat die allemaal een eigen naam hebben. In de onderstaande figuur hebben wij de anatomie van een puls samengevat. De meeste (overdreven voorgestelde) onderdelen hebben uitsluitend een Engelstalige benaming.
- Pre-puls vervorming (pre-pulse distortion).
Komt soms voor op de uitgang van een schakeling als deze schakeling grote looptijdverschillen heeft tussen de diverse harmonischen die in de puls zitten (lees verder). - Voorflank (leading edge).
De tijd die de spanning er over doet om van 10 % tot 90 % van de uiteindelijke grootte te stijgen. Deze tijd noemt men de stijgtijd. - Overshoot.
Ontstaat als een schakeling de hogere harmonischen in de puls meer versterkt dan de lagere harmonischen (lees verder). - Ringing.
Wijst er op dat de schakeling die de puls levert gevoelig is voor hoogfrequent oscillaties. - Amplutude.
Het verschil in volt tussen het lage niveau en het hoge niveau van de puls. - Droop.
Plaatselijke verlaging van de amplitude als gevolg van de kleinere versterking van de lage harmonischen in het signaal (lees verder). - Achterflank (trailing edge).
De tijd die de spanning er over doet om van 90 % tot 10 % van de uiteindelijke grootte te dalen. Deze tijd noemt men de daaltijd. - Backswing.
Een na-ijlen van het signaal als gevolg van looptijdverschillen in de schakeling die de puls verwerkt. - Pulsbreedte (Pulse width).
De tijd die verloopt tussen het moment dat de voorflank 50 % van de amplitude bereikt en het moment dat de achterflank dezelfde waarde bereikt.
 |
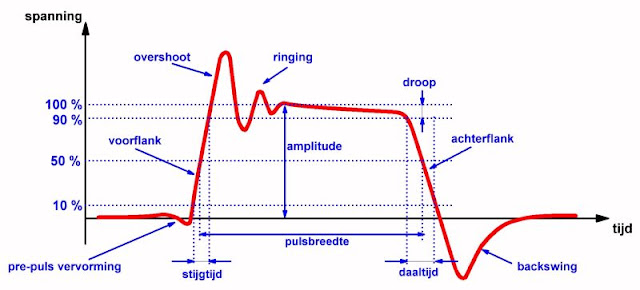| De onderdelen waaruit een puls bestaat. (© 2019 Jos Verstraten) |
Een belangrijke eigenschap van een pulsspanning kan niet in de bovenstaande figuur worden gedefinieerd. De duty-cycle is het percentage in een periode waarin het signaal zijn hoog spanningsniveau heeft. Een periode is uiteraard de tijd die een puls er over doet om één volledige cyclus te voltooien. In de onderstaande figuur hebben wij deze eigenschap van een pulsspanning grafische voorgesteld. Als de puls volledig symmetrisch is in de tijd, dan is de duty-cycle gelijk aan 50 %.
 |
| Het begrip 'duty-cycle' grafisch toegelicht. (© 2019 Jos Verstraten) |
Een andere heel belangrijke grootheid van een zich repeterende pulsvormige spanning is de periode. Dit wordt toegelicht aan de hand van de onderstaande grafiek. De periode of trillingstijd van een repeterend signaal is de tijdsduur tussen twee opeenvolgende momenten waarbij de signaalspanning identiek is. De periode T is het omgekeerde van de frequentie f, en wordt uitgedrukt in seconden uitgedrukt. In formule:
T = 1 / f
of:
f = 1 / T
Een pulsvormig signaal met een periode van 1 milliseconde heeft dus een frequentie van:
f = 1 / 0,001 = 1.000 Hz = 1 kHz
 |
| Het begrip 'periode' grafisch toegelicht. (© 2019 Jos Verstraten) |
Pulsen zult u vaak gebruiken voor het aansturen van digitale IC's van de TTL 74xx- en van de CMOS 40xx-families. Dan moet u rekening houden met de maximale spanningen die u mag gebruiken voor het aanbieden van een 'L' of een 'H' aan een schakeling.
Voor de standaard TTL-schakelingen bedragen deze drempels:
- Kleiner dan 0,4 V voor 'L'.
- Groter dan 2,4 V voor 'H'.
Voor CMOS en de 74HC-familie ligt de drempel in het midden van de voedingsspanning. Voedt u bijvoorbeeld een CD4011 NAND-poort uit 15 V, dan ligt de drempel tussen 'L' en 'H' rond 7,5 V.
 |
| De 'L'- en 'H'-drempels bij standaard-TTL en CMOS. (© 2019 Jos Verstraten) |
De fourier-reeks van een tijdsymmetrische puls
Sinussen optellen levert pulsen op
Het lijkt ongeloofwaardig, maar men heeft aangetoond dat een pulsvormige spanning samengesteld is uit een in theorie oneindig aantal sinusvormige spanningen met allemaal een frequentie die een veelvoud is van de frequentie van de pulsvormige spanning. Een pulsvormige spanning met een frequentie van 1 kHz bestaat dus uit de optelsom van sinusvormige spanningen met frequenties van 1 kHz, 2 kHz, 3 kHz, etc. De onderlinge verhouding van de amplitudes van deze sinusvormige spanningen bepaalt hoe de pulsvormige spanning er uit komt te zien. Zo'n som van sinussen noemt men de 'fourier-reeks' van de puls. De sinussen met een hogere frequentie dan deze van de puls noemt men de 'harmonischen'. Deze theorie werd in de negentiende eeuw ontwikkeld door de Franse wiskundige Fourier en is een van de belangrijkste wiskundige theorieën die in de elektronica worden toegepast.
De fourier-reeks van een tijdsymmetrische puls
Uit deze theorie kunt u afleiden dat een tijdsymmetrische blokvormige spanning is samengesteld uit de volgende harmonische sinussen:
f(x) = sin x + 1/3 sin 3x + 1/5 sin 5x + 1/7 sin 7x + 1/9 sin 9x + ....
Deze wiskunde zegt u misschien helemaal niets, dus laten wij deze formule vertalen naar normale taal.
U krijgt een mooie blokvormige symmetrische puls met een frequentie van 1 kHz als u de volgende sinusvormige harmonische spanningen bij elkaar optelt:
- Een sinus met een frequentie van 1 kHz en een amplitude van 1,000 V.
- Een sinus met een frequentie van 3 kHz en een amplitude van 0,333 V.
- Een sinus met een frequentie van 5 kHz en een amplitude van 0,200 V.
- Een sinus met een frequentie van 7 kHz en een amplitude van 0,142 V.
- Een sinus met een frequentie van 9 kHz en een amplitude van 0,111 V.
- Een sinus met een frequentie van 11 kHz en een amplitude van 0,090 V.
- etc.
U merkt dus op dat de amplitude van de harmonischen steeds kleiner wordt. In de praktijk stelt u vast dat u een vrijwel perfect ogende symmetrische blokspanning krijgt als u alle harmonischen tot en met de twintigste samenvoegt. In onderstaande figuur is voorgesteld hoe het signaal er uit ziet als u de eerste, derde en vijfde harmonischen bij elkaar optelt. U ziet de vorm van de symmetrische blokgolf reeds ontstaan.
 |
| Optellen van oneven harmonischen met de juiste amplituden levert uiteindelijk een blokgolf op. (© 2019 Jos Verstraten) |
 |
| In deze animatie ziet u hoe de fourier-reeks een ideale symmetrische puls vormt. (© LucasVB - Wikimedia Commons) |
Een symmetrische puls als analyse-werktuig
Inleiding
Het zal duidelijk zijn dat een symmetrische puls er anders komt uit te zien als de verhouding tussen de amplituden van de harmonischen verandert. Dank zij dit verschijnsel kunt u een symmetrische puls heel goed gebruiken om snel de eigenschappen van een schakeling te beoordelen. Stuur een mooie symmetrische puls in de schakeling en kijk op uw oscilloscoop hoe de puls uit de schakeling komt. Als de uitgang nog steeds een mooie symmetrische puls levert weet u zeker dat de schakeling alle frequenties tot en met de twintigste harmonische even veel versterkt en dus een goede bandbreedte heeft. Om te testen of een audioversterker alle hoorbare frequenties even goed versterkt volstaat het dus een paar symmetrische pulsen met diverse frequenties aan de ingang aan te bieden. Stuurt u een puls met een frequentie van 1 kHz in de versterker en komt deze puls onvervormd uit de uitgang? Dan weet u zeker dat de versterker goed werkt tot 20 kHz, immers de twintigste harmonische van de pulsfrequentie van 1 kHz.
Verzwakking van de hoge frequenties
Als de puls aan de uitgang van de schakeling er ongeveer uitziet als voorgesteld in het onderstaande oscillogram weet u zeker dat de geteste schakeling de hoge harmonischen uit de puls minder versterkt en de hoog-weergave dus slecht is. Hoe minder steil de voor- en achterflanken verlopen, hoe meer de hogere harmonischen verzwakt zijn.
 |
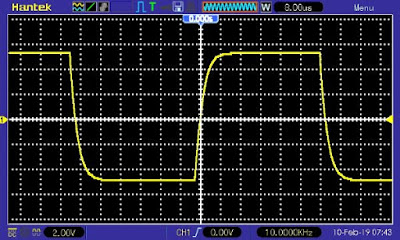| De typische vorm van een symmetrische puls waarvan de hogere harmonischen verzwakt zijn. (© 2019 Jos Verstraten) |
Als de uitgangspuls van uw schakeling veel 'droop' vertoont, zoals voorgesteld in onderstaand oscillogram, dan betekent dit dat uw schakeling de lage harmonischen uit de puls verzwakt en de bassen dus niet goed versterkt worden.
 |
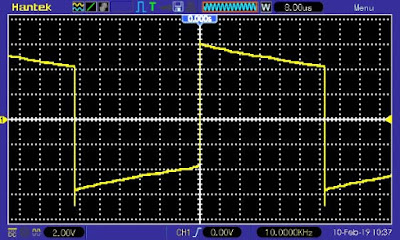| Zo ziet een puls er uit als de lage harmonischen verzwakt zijn. (© 2019 Jos Verstraten) |
Gevaar voor oscillaties
Als de uitgangspuls van uw schakeling veel last heeft van 'ringing', zie onderstaand oscillogram, dan betekent dit dat er in uw schakeling verborgen inductanties aanwezig zijn en dat het gevaar bestaat dat uw schakeling gaat oscilleren. In audio eindversterkers kan dit, in het slechtste geval, leiden tot het doorbranden van de eindtransistoren.
 |
| Ringing op een puls wijst op het gevaar van oscillaties in uw schakeling. (© 2019 Jos Verstraten) |
Digitale metingen met pulsen
Stijgtijden meten met een puls
Een mooie puls met een steile voorflank is een ideaal hulpmiddel voor het meten van de stijgtijd van analoge en digitale schakelingen. In de meeste gevallen geldt dat een kleine stijgtijd beter is dan een grote. Leg de 'ideale' puls aan de ingang van uw schakeling en sluit de uitgang van de schakeling aan op uw scope. De meeste moderne scope's hebben de mogelijkheid om zowel horizontale als verticale cursors in te stellen. Zet de horizontale cursors op 10 % en 90 % van de signaalamplitude. Deze lijnen snijden de trace van het uitgangssignaal op twee plaatsen. Zet de verticale cursors op deze twee snijpunten. U kunt nu de stijgtijd van uw schakeling aflezen van het scherm.
 |
| Het meten van de stijgtijd van een schakeling met een steile puls. (© 2019 Jos Verstraten) |
Niets in de natuur verloopt traagheidsloos, behalve dan sommige nog onbegrepen kwantummechanische verschijnselen. Als u dus een puls aan een schakeling aanlegt, dan zal het een bepaalde tijd duren alvorens deze puls op de uitgang van de schakeling verschijnt. De tijd tussen het aanleggen van de puls aan de ingang en het verschijnen van de response van de schakeling op de uitgang noemt men de vertragingstijd of de doorlooptijd. In het onderstaande oscillogram hebben wij bijvoorbeeld de vertragingstijd gemeten tussen het in- en het uitgangssignaal van een vrij uitgebreide logische schakeling. Beide signalen worden aangeboden aan de twee ingangen van een scope. De gevoeligheden en de posities van beide kanalen worden zo afgeregeld dat beide signalen even groot zijn en dat de massa-referenties van beide signalen samenvallen. Met de cursor-functie van de scope kunt u nu de twee verticale cursors laten samenvallen met de punten waar beide signalen een horizontale lijn snijden. U kunt dan de vertragingstijd van de schakeling van het scherm aflezen.
 |
| Het meten van de signaalvertraging van een schakeling door het vergelijken van de in- en de uitgangspuls. (© 2019 Jos Verstraten) |
EMEC Breakdown-voltage tester
