|
Analoge bandfilters werken alleen in op een smalle frequentieband uit een signaal. Bandfilters kunt u indelen in banddoorlaat filters, bandsper filters en equaliser filters.
|
Algemene achtergrondinformatie noodzakelijk
Zeggen termen als amplitude-karakteristiek, afsnijfrequentie, dB/octaaf, tweede orde filter, Bode-plot en Butterworth filter u niets? Dan raden wij u ten stelligste aan eerst het artikel Know-how: analoge filterschakelingen te lezen. In dat artikel maakt u kennis met algemene begrippen uit de analoge filtertechniek die ook in dit artikel aan de orde zullen komen.
Het banddoorlaat filter
Inleiding
U kunt banddoorlaat filter in twee grote groepen indelen:
- Smalbandige filters.
- Breedbandige filters.
Het verschil tussen beide filters is getekend in de onderstaande figuur. Links is een smalbandig filter getekend, rechts een breedbandig. Waar de definitie van een smalbandig filter eindigt en deze van een breedbandig filter begint is moeilijk aan te geven. In de meeste gevallen houdt men het erop dat een breedbandig filter een 'plat dak' in zijn amplitude-karakteristiek heeft.
 |
| Een smalbandig en een breedbandig banddoorlaat filter. (© 2020 Jos Verstraten) |
Er bestaat een bepaald frequentiegebied waarvoor de versterking van het filter maximaal is. Deze versterking wordt meestal gelijk gesteld aan 0 dB. De voornaamste eigenschap van een banddoorlaat filter is de bandbreedte B. Dit is het frequentiegebied waarvoor de verzwakking van het filter kleiner is dan 3 dB, gemeten ten opzichte van de centrale filterfrequentie fo. In de bovenstaande grafieken wordt de bandbreedte dus gedefinieerd door het gebied tussen de frequenties fl en fh. Het zal duidelijk zijn dat de bandbreedte kleiner wordt naarmate het filter smalbandiger wordt.
De steilheid van een banddoorlaat filter
Een andere belangrijke eigenschap van een banddoorlaat filter is de steilheid. Dat is de helling waarmee signalen met frequenties die buiten de bandbreedte liggen worden verzwakt. De mate van de gewenste steilheid is afhankelijk van de toepassing van het banddoorlaat filter. Gebruikt u een aantal identieke banddoorlaat filter om een frequentie-afhankelijk LED-display samen te stellen, waarbij op een aantal LED-kolommen de frequentie-samenstelling van een LF-signaal wordt geobserveerd, dan moet de steilheid van de filters zo groot mogelijk zijn. Dit wordt toegelicht aan de hand van de grafieken in de onderstaande figuur. In de bovenste grafiek is de ideale respons van vier bandfilters getekend. De filters hebben een oneindig grote steilheid, het gehele frequentiegebied wordt keurig zonder overlapping door de vier banddoorlaat filters opgesplitst in vier deelgebieden.
In de onderste grafiek zijn de amplitude-karakteristieken getekend van vier banddoorlaat filters met een geringe steilheid. Deze karakteristieken hebben een grote overlapping, waardoor een signaal met een welbepaalde frequentie in twee meetgebieden zal terecht komen, hetgeen de meetresultaten vertroebeld.
 |
| Het begrip steilheid toegelicht aan de hand van een voorbeeld. (© 2020 Jos Verstraten) |
Gebruikt u echter bandfilters om een geluidssignaal op te splitsen in een aantal banden die de kanalen van een lichtorgel sturen, dan is het niet nodig en zelfs ongewenst om erg steil te filteren. Dit wordt toegelicht in de grafiek van de onderstaande figuur. Bij dergelijke toepassingen moet u de bandfilters zó ontwerpen dat zij elkaar overlappen. Dit bevordert het bij een lichtorgel gewenste kleurenspel in functie van de frequenties van het muzieksignaal.
 |
| Banddoorlaat filters voor een frequentie-selectief lichtorgel. (© 2020 Jos Verstraten) |
Een breedbandig filter ontstaat als u, zoals getekend in de onderstaande figuur, een hoog- en een laagdoorlaat filter in de juiste volgorde in serie schakelt. Zoals uit de amplitude-karakteristiek volgt zijn er nu twee afsnijfrequenties fl en fh. Deze bepalen de bandbreedte B van de schakeling. De frequentie fh is de afsnijfrequentie van het hoogdoorlaat filter, fl is de afsnijfrequentie van het laagdoorlaat filter. Het zal duidelijk zijn dat de schakeling alleen als banddoorlaat filter werkt als fh kleiner is dan fl. U moet de karakteristieken van beide deelfilters uiteraard nauwkeurig op elkaar afstemmen. Dat betekent dat u voor beide filters hetzelfde filter-concept moet toepassen. Welk concept u kiest is afhankelijk van de steilheid die u aan het filter wilt toekennen. Voor zeer steile filters moet u uiteraard een beroep doen op het Chebyshev-concept.
 |
| Het breedbandig banddoorlaat filter. (© 2020 Jos Verstraten) |
Vaak is het gewenst één bepaalde frequentie uit een breed spectrum te filteren. Brede banddoorlaat filters zijn hiervoor niet geschikt. In principe is het mogelijk de bandbreedte van de beschreven schakeling te verkleinen. Maar dan moet u zeer scherp afsnijdende hoog- en laagdoorlaat filters gebruiken, dus minstens werken met vierde orde filters. Dat betekent dat u vier operationele versterkers moet toepassen. De schakeling wordt dan zeer complex en het afstemmen van de karakteristieken van beide filters is alles behalve eenvoudig.
Maar er bestaan gelukkig eenvoudigere schakelingen! In de onderstaande figuur is een scherp banddoorlaat filter met slechts één operationele versterker getekend. De schakeling vertoont erg veel overeenkomst met een sinusoscillator die werkt volgens het principe van de Wien-brug. De frequentie waarop het filter staat afgesteld wordt bepaald door de onderdelen C1, C2, R2 en R3 en wel volgens de uitdrukking:
fo = 1 / [2 ● π ● R ● C]
waarbij:
R = R2 = R3
C = C1 = C2
 |
| Een eenvoudig smalbandig banddoorlaat filter. (© 2020 Jos Verstraten) |
A = 1 + [R6 / (R4 + R5)]
De versterkingsfactor moet in ieder geval kleiner zijn dan drie. Bij een grotere waarde gaat de schakeling namelijk niet als filter werken, maar als oscillator. Vandaar dat het noodzakelijk is een van de genoemde weerstanden als instelpotentiometer uit te voeren. Zoals blijkt uit de bovenstaande figuur is de amplitude-karakteristiek van het filter afhankelijk van de instelling van de versterkingsfactor. Hoe meer de versterking de kritische maximale waarde van drie benadert, hoe scherper het filter zal zijn en hoe groter de versterking op de resonantiefrequentie fo.

Een smalle frequentieband uitfilteren
Als u niet een bepaalde frequentie, maar een smalle frequentieband uit een spectrum moet filteren, dan kunt u twee identieke schakelingen achter elkaar schakelen, ieder afgestemd op een iets andere filterfrequentie. Het schema is getekend in de onderstaande figuur. Afhankelijk van de afregeling van de potentiometers R7 en R14 kunt u een doorlaat-karakteristiek met een vlakke top of met twee maxima instellen.
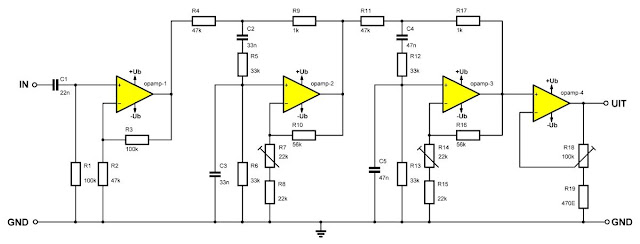 |
| Het uitfilteren van een smalle frequentieband. (© 2020 Jos Verstraten) |
 |
| De amplitude-karakteristiek van de beschreven schakeling. (© 2020 Jos Verstraten) |
Een andere, vaak toegepaste schakeling voor een banddoorlaat filter is getekend in de onderstaande figuur. Deze schakeling heeft als groot voordeel dat u door de verhouding tussen twee weerstanden te variëren de waarde van de bandbreedte over een factor tien kunt instellen. U kunt dit schema dus zowel toepassen voor zeer smalbandige filters als voor breedbandige schakelingen.
 |
| Een banddoorlaat filter met instelbare bandbreedte. (© 2020 Jos Verstraten) |
De filterfrequentie wordt bepaald door de formule:
fo = 1 / [2 ● π ● C ● √ (R1 ● R4)]
waarbij de waarde van de condensatoren C2 en C3 identiek wordt gekozen en gelijk gesteld aan C. Alle karakteristieken van deze schakeling zijn afhankelijk van de verhouding tussen de weerstanden R1 en R4. Dit verband is gegeven in de tabel naast het schema. Hieruit blijkt dat u de bandbreedte rond de filterfrequentie fo kunt variëren van 2 kHz (zeer breedbandig) tot ongeveer 350 Hz (smalbandig).
Het berekenen van deze schakeling is de eenvoud zelve. Stel dat u een filter moet ontwerpen met een centrale frequentie fo van 1 kHz en een bandbreedte van 500 Hz. Uit de tabel volgt dat de verhouding tussen beide weerstanden gelijk moet zijn aan 16, zodat u kunt besluiten dat R4 = 16 ● R1. Stel dat u voor beide capaciteiten een condensator van 5 nF kiest. Uit de formule van de centrale frequentie kunt u dan berekenen dat R1 = 7,95 kΩ en R4 = 127,2 kΩ. In de praktijk worden de onderdelenwaarden uiteraard afgerond naar 4,7 nF, 8 kΩ en 128 kΩ.
Banddoorlaat filter met eenvoudige bandbreedte regeling
In de onderstaande figuur is het schema getekend van een banddoorlaat filter, waarmee u op een zeer eenvoudige manier de bandbreedte continu kunt regelen. U herkent de twee weerstanden en twee condensatoren die de bekende Wien-configuratie vormen. De bandbreedte wordt geregeld door de mate van versterking van de operationele versterker in te stellen. Dit gebeurt uiteraard met R1 want deze zit, samen met weerstand R2, in de terugkoppellus van de operationele versterker. Bij een te grote mate van terugkoppeling gaat de schakeling niet als filter werken, maar als oscillator. In de meeste gevallen moet u in de praktijk een vaste weerstand in serie met de potentiometer opnemen, geschakeld tussen de uitgang van de operationele versterker en de bovenste aansluiting van de potentiometer. Op deze manier kunt u de maximale versterking begrenzen op een veilige waarde.
In de tabel naast het schema zijn de specificaties van de schakeling samengevat voor verschillende waarden van α, een factor die de verhouding tussen de weerstanden in het terugkoppelnetwerk bepaalt. Voor kleine waarden van α veranderen de eigenschappen van de schakeling niet zo snel. Als α echter in de buurt komt van 0,45 gaan de bandbreedte en de versterking erg snel variëren. Vandaar dat het in de praktijk aanbeveling verdient om voor de potentiometer R1 een exemplaar met omgekeerde logaritmische karakteristiek toe te passen. Een dergelijke potentiometer kunt u maken door een gewone logaritmische potentiometer omgekeerd aan te sluiten.
 |
| Een banddoorlaat filter waarbij de bandbreedte met behulp van een potentiometer wordt ingesteld. (© 2020 Jos Verstraten) |
Het bandsper filter
Inleiding
Net zoals bij banddoorlaat filters kunt u ook bij bandsper filters onderscheid maken tussen brede en smalle filters. De brede filters kunnen weer samengesteld worden uit een combinatie van een laagdoorlaat en een hoogdoorlaat filter. Voor smalle bandsper filters zijn weer schakelingen beschikbaar die gebruik maken van slechts één operationele versterker.
Een breedbandig bandsper filter
Het basisprincipe van een dergelijk filter is getekend in de onderstaande figuur. Het laagdoorlaat filter en het hoogdoorlaat filter zijn nu min of meer parallel geschakeld. Het signaal wordt door de twee filters gestuurd. De uitgangen van de twee filters gaan nu echter naar een inverterende sommeerversterker. De amplitude-karakteristiek van een dergelijk filter is in dezelfde figuur voorgesteld. Ook nu zijn er twee afsnijfrequenties aanwezig. Het grote verschil met het banddoorlaat filter is echter dat de afsnijfrequentie van het hoogdoorlaat filter nu groter is dan deze van het laagdoorlaat filter.
 |
| Een breedbandig bandsper filter. (© 2020 Jos Verstraten) |
Het basisschema van een smalbandig bandsper filter is getekend in de onderstaande figuur. De dimensionering van de onderdelen zet de sperfrequentie op 60 Hz. De operationele versterker is als spanningsvolger geschakeld en koppelt de uitgangsspanning terug naar het filter netwerk. Het filter bestaat uit drie weerstanden en drie condensatoren, die onder de vorm van twee T-netwerken parallel geschakeld worden. De uitgang van het filternetwerk is het knooppunt van de weerstand R3 en de condensator C3. Door de terugkoppeling via de operationele versterker, een techniek die 'bootstrapping' wordt genoemd, wordt de kwaliteitsfactor opgevoerd tot 50.
 |
| Een smalbandig bandsper filter. (© 2020 Jos Verstraten) |

Berekenen van de filterfrequentie
De berekening van de filterfrequentie is erg eenvoudig. Over het algemeen neemt men aan dat:
R1 = R2 = 2 ● R3
en
C1 = C2 = C3 / 2
Onder deze voorwaarden wordt de centrale filterfrequentie gegeven door de formule:
fo = 1 / [2 ● π ● R1 ● C1]
Bandsper filter met eenvoudige bandbreedte regeling
Door de mate van terugkoppeling te variëren kunt u de eigenschappen van het filter beïnvloeden. Maar dan moet u wel, zoals getekend in de onderstaande figuur, een tweede operationele versterker inschakelen. De tweede operationele versterker is noodzakelijk omdat het knooppunt tussen R3 en C3 uit een zo laag mogelijke en constante impedantie aangestuurd moet worden. Zonder de tweede operationele versterker zou de loperweerstand van R4 een rol spelen bij de karakteristieken van het netwerk. Hetgeen tot gevolg zou hebben dat de filterfrequentie afhankelijk wordt van de instelling van de bandbreedte.
De operationele versterker zorgt nu echter voor een te verwaarlozen impedantie, zodat het afregelen van de kwaliteitsfactor geen invloed heeft op de waarde van de filterfrequentie. Met de getekende schakeling kunt u de kwaliteitsfactor van het bandsper filter variëren tussen 0,3 en 50. Hetgeen, grafisch bekeken, ongeveer overeen komt met de twee uiterste bandbreedtes (rood en groen) die in de bovenstaande grafiek zijn voorgesteld.
 |
| Een bandsper filter met instelbare bandbreedte. (© 2020 Jos Verstraten) |
Het equaliser filter
Inleiding
Een equaliser filter is een schakeling die de eigenschappen van een banddoorlaat filter combineert met deze van een bandsper filter. Bovendien kunt u met behulp van één potentiometer overschakelen van bandsper naar banddoorlaat. Uiteraard is dat een continu proces, zodat er een stand van de potentiometer is waarbij het filter noch versterkt, noch verzwakt. Dergelijke filters worden uiteraard gebruikt in equalisers, waarbij het mogelijk is de weergave van het volledige audiobereik van 20 Hz tot 20 kHz met behulp van diverse potentiometers in te stellen. Op deze manier kunt u de amplitude-karakteristiek van een versterker heel nauwkeurig aanpassen aan de akoestische eigenschappen van een kamer of een zaal.
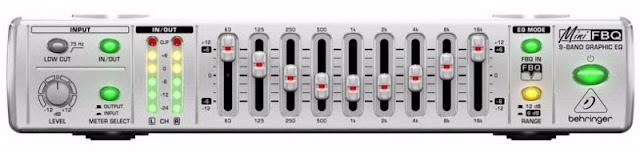 |
| Een commerciële equaliser. (© www.bax-shop.nl) |
De amplitude-karakteristiek van een dergelijk filter is getekend in de onderstaande figuur. Duidelijk blijkt hieruit dat de curves, die ieder overeen komen met één stand van de potentiometer, zeer symmetrisch verlopen en dat het filter één instelling heeft (zwart) waarbij de amplitude volledig vlak verloopt.
 |
| De amplitude-karakteristiek van een equaliser filter. (© 2020 Jos Verstraten) |
De basisschakeling van een dergelijk filter is getekend in de onderstaande figuur. De condensatoren C1 en C2 bepalen de filterfrequentie. De lineaire potentiometer R2 stelt de verzwakking of versterking in. In de middenstand werkt de schakeling als lineaire versterker. De bandbreedte van het filter is afhankelijk van de verhoudingen tussen de beide condensatoren en tussen R1 en R2.
Vaak gaat men uit van een condensator verhouding C1/C2 = 15 en een weerstand verhouding R2/R1 = 10.
Als de weerstand verhouding stijgt zal de bandbreedte van het filter smaller worden, maar zal meer versterkt en verzwakt worden. Voor audio-toepassingen wordt de verhouding van 10 als ideaal gezien.
Een grotere verhouding tussen beide condensatoren vergroot de bandbreedte en heeft minder versterking en verzwakking tot gevolg.
 |
| De basisschakelíng van een equaliser filter. (© 2020 Jos Verstraten) |
De bedoeling is verschillende schakelingen, ieder met een eigen filterfrequentie, te combineren. Op deze manier kunt u het volledige audiobereik opsplitsen in een aantal banden, die ieder door een equaliser filter worden verzwakt of versterkt. De totale amplitude-karakteristiek ziet er dan uit zoals getekend in de onderstaande figuur.
In dit voorbeeld worden de filterfrequenties ingesteld op:
- 31,5 Hz.
- 63 Hz.
-125 Hz.
-250 Hz.
-500 Hz.
-1 kHz.
-2 kHz.
-4 kHz.
-8 kHz.
-16 kHz.
Deze frequenties zijn niet willekeurig gekozen, maar liggen één octaaf uit elkaar. In dit geval spreekt men dan ook van een 'octaaf-equaliser'.
 |
| De amplitude-karakteristiek van een schakeling met tien equaliser filters. (© 2020 Jos Verstraten) |
Er bestaan twee systemen om de individuele filters met elkaar te combineren:
- De seriële schakeling.
- De parallelle schakeling.
De seriële equaliser
Bij de seriële schakeling, waarvan het principe is getekend in de onderstaande figuur, staan alle filters achter elkaar geschakeld. Het signaal doorloopt alle filters en ieder filter pikt uit het totale frequentiespectrum die band uit, waarop het is afgestemd. De reeds voorgestelde schakeling van is ideaal voor deze seriële oplossing. De uitgang van een filter gaat immers naar de niet-inverterende ingang van de volgende operationele versterker. Deze ingang heeft een zeer hoge impedantie, zodat het filter niet belast wordt door de volgende schakeling en de filter-karakteristieken zich niet onderling kunnen beïnvloeden. Omdat de schakeling bovendien gelijkspanningsgekoppeld is (tussen de inverterende ingang van de operationele versterker en de uitgang staan alleen maar weerstanden) kunt u door middel van één spanningsdeler aan de niet-inverterende ingang van de eerste operationele versterker het gehele netwerk instellen op de helft van de voedingsspanning.
Dit uiteraard in de veronderstelling dat u niet symmetrisch voedt. U moet het signaal dan uiteraard via een scheidingscondensator aan de eerste trap aanbieden. De laatste trap wordt afgesloten met een als buffer geschakelde operationele versterker, zodat ook dit laatste filter niet wordt belast.
 |
| Het principe van de seriële equaliser. (© 2020 Jos Verstraten) |
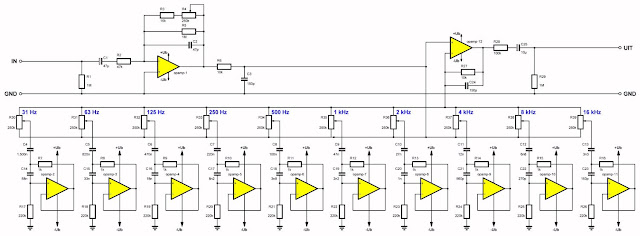
Bij de parallelle schakeling, principieel voorgesteld in de onderstaande figuur, staan alle filters parallel geschakeld. Alle ingangen worden via een buffertrap aangestuurd met het ingangssignaal. De uitgangen van de diverse filters gaan naar een mengschakeling met virtueel massapunt. Op deze manier kunnen de filters elkaar niet beïnvloeden. Het zal nu echter wel duidelijk zijn dat u ieder filter een eigen instelling moet geven. Beter is natuurlijk de gehele schakeling symmetrisch te voeden, waardoor alle trappen kunnen worden ingesteld ten opzichte van de massa.
 |
| Het principe van de parallelle equaliser. (© 2020 Jos Verstraten) |
In de onderstaande figuur is het praktische schema getekend van een parallel werkende equaliser met tien banden. Vanwege de parallelle structuur van de schakeling zijn de eigenlijke filters anders uitgevoerd dan volgens het eerder voorgestelde principeschema zou moeten. Duidelijk blijkt dat de filtersecties nu niet mooi symmetrisch zijn opgebouwd. Vanwege dat feit verdient de seriële structuur de voorkeur.