
|
In dit artikel beschrijven wij de wonderbaarlijke technieken die men heeft bedacht om die grote datacompressie bij het digitaliseren van een film te realiseren: van 160 Mbit/s naar 1,14 Mbit/s.

|
Een historische inleiding
Digitaal verzenden van data heeft beperkingen
Toen de elektronica industrie in het begin van de jaren tachtig begon te filosoferen over digitale communicatie werd al snel duidelijk dat het nooit zou lukken foto's, video en audio ongecomprimeerd te versturen. Immers, een gedigitaliseerde foto met een resolutie van 1.024 bij 1.024 pixels en met een kleurendiepte van 24 bit, een minimale vereiste voor professioneel kleurendrukwerk, neemt ongeveer 3 MB aan opslagruimte in beslag. Nu waren er wel een heleboel compressietechnieken ontwikkeld, maar de internationale industrie was er gelukkig van overtuigd dat er één wereldstandaard voor de compressie van digitale audio en video moest worden afgesproken. Die standaard zou flexibel moeten zijn, zodat een en dezelfde hardware door software geprogrammeerd kon worden voor verschillende soorten compressie algoritmen. Op deze manier zou de internationale standaard zonder grote problemen aangepast kunnen worden aan verschillende toepassingen, die ieder hun eigen eisen stelden.
JPEG
Op initiatief van twee internationale normeringsinstituten, de ISO (International Standardisation Organisation) en de IEC (International Electrotechnical Committee) werd in 1988 een internationale werkgroep opgericht met als naam 'Joint Photographic Expert Group'. Deze werkgroep ging door het leven onder de naam 'JPEG' en was samengesteld uit internationaal toonaangevende experts op het gebied van compressie technieken en digitale beeldverwerking. De werkgroep ontwikkelde op korte termijn een beeldcompressie techniek, die geschikt was voor een breed scala van toepassingen met verschillende kwaliteiten, resoluties, compressieniveaus en kleurmodellen. Deze techniek kreeg ook de naam 'JPEG' en werd beschreven in de ISO/IEC-norm 10.918.
JPEG werd ontwikkeld voor de compressie van statische beelden zoals krantenfoto's. Daarvoor wordt het algoritme nu nog steeds gebruikt. Vrijwel alle foto's en illustraties op Internet staan in .JPG-formaat, een rechtstreekse afgeleide van de JPEG-standaard. Natuurlijk dacht men er wel aan deze techniek ook toe te passen voor het comprimeren van dynamische beelden, dus video. In de begintijd van deze techniek waren de noodzakelijke processoren echter niet snel genoeg om beelden in real time te comprimeren en nadien weer te decomprimeren.
Lossy en lossless JPEG
Alvorens de MPEG compressietechniek te bespreken moet er nog een opmerking over de JPEG-standaard worden gemaakt. De standaard beschrijft twee compressieschema's:
- Lossy.
- Lossless.
Bij de lossy techniek zal het beeld dat wordt teruggewonnen uit de compressiegegevens niet identiek zijn aan het originele beeld. Er worden dus bij de compressie gegevens verwijderd. Nu valt dat nauwelijks op, omdat het menselijk oog een vrij ongevoelig instrument is. Zo is het oog zeer ongevoelig voor kleine nuances in kleur. Van deze wetenschap wordt bij de lossy techniek gebruik gemaakt om zeer hoge datareducties te verkrijgen.
 |
| Een foto als lossy JPG met diverse compressiefactoren. (© 2004 BenTheWikiMan) |
De ontwikkeling van beeldopslag op compact disks noopte de ontwikkelaars om ook voor video een compressie algoritme te ontwikkelen. De uitdaging was groot. De originele CD had immers een maximale datasnelheid van slechts 1,411 Mbit/s. Voor het aangaan van deze uitdaging werd een nieuwe internationale werkgroep opgericht, die deze keer de naam 'Moving Picture Expert Group' kreeg, afgekort tot MPEG.
Natuurlijk is het duidelijk dat deze werkgroep voort borduurde op de JPEG-technologie. Het grote verschil tussen JPEG en MPEG is dat JPEG beeldje voor beeldje comprimeert, zonder rekening te houden met de samenstelling van een vorig en/of volgend beeldje. MPEG doet dat wél en bereikt een zeer grote datareductie door alle gegevens die hetzelfde zijn in opeenvolgende beeldjes simpelweg te negeren, of beter uitgedrukt, maar één keer te comprimeren en te verzenden in een zogenoemd referentiebeeld. Nadien worden alleen de verschillen tussen opeenvolgende beeldjes opgezocht en verzonden in verschilbeeldjes. Deze techniek noemt men 'motion compensation' en het zal wel duidelijk zijn dat hierdoor een immense datareductie wordt verkregen. Nadat de originele videobeeldjes op deze manier zijn omgezet in weinig (omvangrijke) referentiebeeldjes en veel (minder omvangrijke) verschilbeeldjes worden op sommige beeldjes de JPEG-algoritmen losgelaten.
Hierbij heeft men gekozen voor de lossy techniek, omdat het kwaliteitsverlies bij bewegende beelden nog veel minder opvalt dan bij statische beelden. Door een combinatie van de lossy JPEG-techniek en de motion compensation MPEG-techniek en enige compromissen wat betreft resolutie en kleursamenstelling van het beeld is men in staat video die bestaat uit 25 beeldjes per seconde te verzenden met een datastroom van maximaal 1,2 Mbit/s.
Diverse MPEG compressie algoritmen
MPEG is een universele compressiestandaard voor video en audio, waarvan in de loop der technische evolutie diverse versies zijn verschenen, met steeds meer mogelijkheden.
- MPEG-1
Versie 1 uit 1991 is de initiële compressiestandaard voor video en audio, opgesteld door de 'Moving Picture Experts Group'. Later werd deze gebruikt als standaard voor video-CD. Het formaat beschrijft ook het populaire Layer 3 (MP3) audiocompressie formaat dat nu nog steeds overal wordt gebruikt voor het gecomprimeerd verzenden van audiostreams. - MPEG-2
Het MPEG-2 formaat is voornamelijk ontwikkeld voor het transporteren van digitale kwalitatief hoogwaardige video en audio voor TV. Het wordt gebruikt voor digitale televisie via conventionele aardse antennes (DVB-T), uitzending via de satelliet (DVB-S) en voor digitale kabeltelevisie (DVB-C). Als u een abonnement hebt op kabel-TV van Ziggo, dan komen de videostreams via MPEG-2 in uw meterkast. Het formaat ondersteunt ook diverse surround sound systemen en is neerwaarts compatibel met MPEG-1. - MPEG-4
Werd geïntroduceerd eind 1998, de standaard werd vastgelegd door de 'Moving Picture Experts Group' als ISO/IEC JTC1/SC29/WG11 onder de formele standaard ISO/IEC 14496. MPEG-4 wordt gebruikt voor compressie van video voor streaming toepassingen. Het op dit moment zeer bekende MP4-formaat, waarmee u digitale video op al uw beeldschermen kunt bekijken is een afgeleide van deze MPEG-standaard.
 |
| Het MPEG-logo dat gereserveerd is voor apparatuur dat MPEG-streams kan verwerken. (© worldvectorlogo) |
De compressie technologieën bij MPEG-1
De algemene structuur van MPEG-1
In dit artikel gaan wij de video compressie technieken bespreken die bij MPEG-1 worden toegepast. Deze technieken zult u ook onder de een of andere aangepaste vorm terugvinden bij alle overige MPEG-formaten.
Bij het comprimeren van filmmateriaal moet de compressietechniek rekening houden met drie zaken:
- De compressie van de video-informatie.
- De compressie van de audio-informatie.
- De synchronisatie tussen video en audio.
Dit laatste is een belangrijk punt, omdat de gegevens naar een seriële code worden omgezet is die synchronisatie niet vanzelf sprekend. Toch is het de bedoeling dat de herwonnen gegevens een lipsynchrone film opleveren!
Het algemene schema van een codering volgens MPEG-1 is samengevat in de onderstaande figuur. Er zijn twee coders, een voor de video en een voor de audio, een systeemklok en een multiplexer die zorgt dat de gecomprimeerde video- en audiogegegevens op de juiste manier tot een seriële datastroom worden gecombineerd.
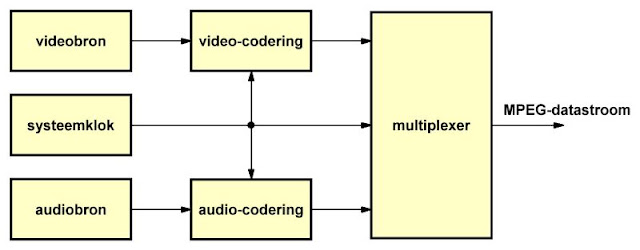 |
| Het algemene schema van een MPEG-1 codering. (© 2019 Jos Verstraten) |
De gegevens worden verpakt in blokken die 'pack's' worden genoemd. In één pack kunnen video- en audio-gegevens worden gemengd. Ieder pack wordt voorafgegaan door een zogenaamde 'header', waarin de voor het decodeersysteem noodzakelijke gegevens over het soort gegevens in het pack en de toegepaste compressie algoritmen worden verwerkt. Een pack bestaat uit verschillende zogenaamde 'packet's', die weer voorafgegaan worden door een subheader en die alleen video- of audiogegevens bevatten. Dat algemene verzendschema is samengevat in de onderstaande figuur en wordt in detail besproken in het vervolg van dit artikel.
In de packet headers worden 'Presentation Time Stamps' opgenomen als tijdreferentie. Deze geven de waarde van de systeemclock weer op het moment dat de gegevens aan de coderingsschakeling worden aangeboden. In de pack header wordt bovendien een 'System Clock Reference' opgenomen. Aan de hand van deze gegevens kan de decodeerelektronica de clock herwinnen en kan ervoor worden gezorgd dat de video- en audiogegevens weer volledig worden gesynchroniseerd.
 |
| De structuur van de gemultiplexte video- en audiogegevens in de seriële datastroom. (© 2019 Jos Verstraten) |
Zoals reeds geschreven heeft MPEG-1 een open structuur. De coderings- en decoderingshardware is in staat verschillende soorten compressie schema's en algoritmen door te voeren. De gebruikte algoritmen worden gecodeerd en in de 'headers' verzonden. Op deze manier is het mogelijk dat een met MPEG-1 gecomprimeerde film van leverancier X na decodering een betere kwaliteit levert dan dezelfde film, gecodeerd door leverancier Y. De kwaliteit van de herwonnen gegevens wordt immers in hoge mate bepaald door de compressie algoritmen die worden gebruikt. Die open architectuur maakt het bovendien ook mogelijk dat bepaalde leveranciers over gaan tot het versleutelen van de gegevens. Aan de decoderzijde kan men dan alleen via een gehuurde of gekochte softwaresleutel de gegevens tot een te bekijken beeld herleiden.
De MPEG-1 codering van video
Datacompressie met een factor 140
De zware taak waar de bedenkers van het systeem voor gesteld stonden was het reduceren van de datastroom met een factor van meer dan 140. De MPEG-1 norm schrijft immers een maximale gegevensstroom van 1,411 Mbit/s voor, zodat de gegevens op een CD passen.
Zoals bekend bestaat een traditionele film uit een filmstrook die tienduizenden beeldjes bevat. Die beeldjes worden met een snelheid van 24 beeldjes per seconde op het scherm geprojecteerd.
Deze analoge filmbeeldjes worden een na een gescand met een resolutie van 480 lijnen die ieder 720 pixels bevatten. Dit is in ieder geval de Amerikaanse norm. Per pixel worden geen 3 x 8, maar slechts 16 bit gebruikt (zie later). Per beeld levert dat ongeveer 5,5 Mbit aan gegevens op. Als men 25 beelden per seconde wil versturen, de Europese TV-standaard, heeft men daarvoor ongeveer 138 Mbit nodig! Natuurlijk moet men nog allerlei coderings en compressie gegevens meesturen, zodat één seconde video een datastroom van ongeveer 160 Mbit oplevert. Een CD kan echter (afgerond naar een veilige ondermarge en rekening houdende met ruimte voor de audio) slechts ongeveer 1,15 Mbit/s verwerken. De gegevens moeten dus met een factor 140 worden gecomprimeerd! Het zal duidelijk zijn dat een dergelijke zware compressie niet in één stap is te realiseren.

Datareductie in dertien bewerkingen
De codering van de videogegevens is erg ingewikkeld en doorloopt een heleboel stapjes. In de meeste bewerkingen wordt iets bijgedragen aan de totale compressie, zodat uiteindelijk toch de noodzakelijke totale compressiefactor wordt verkregen. In het kort komt de MPEG verwerking van een analoog filmsignaal naar de uiteindelijke gecomprimeerde datastroom neer op de volgende procedure:
- Stap 1
Scannen van de filmbeelden met 3 x 8 bit volgens het RGB-kleurenschema en met een resolutie van 720 bij 480 pixels. - Stap 2
Intelligent reduceren van de horizontale en verticale resolutie met een factor twee (compressieslag 1). - Stap 3
Omzetten van de RGB-gegevens naar een YUV-schema en intelligente reductie van de chrominantie gegevens (compressieslag 2). - Stap 4
Indelen van het beeld in 'macroblokken' van 8 bij 8 pixels. - Stap 5
Opslaan van een groot aantal macroblokken van opeenvolgende beeldjes in een geheugen - Stap 6
Toepassen van 'motion compensation' door middel van 'motion vector' en 'prediction error'. - Stap 7
Verdelen van de videostroom in zogenoemde I-, P- en B-frames en toepassen van 'forward prediction' en 'bidirectional prediction'. - Stap 8
Berekenen van 'motion vectors' (compressieslag 3). - Stap 9
Toepassen op de macroblokken van de I-beelden van 'DCT', afkorting van 'discrete cosinus transformatie'. - Stap 10
De zuiver wiskundige gegevens die hieruit voortkomen onderwerpen aan een 'psychovisuele quantiseringsmatrix', waardoor de lossy compressie van JPEG ontstaat (compressieslag 4). - Stap 11
De JPEG gecomprimeerde gegevens van de I-frames weer combineren met de gegevens van de P- en B-frames en deze in een bepaalde volgorde samenvoegen tot één datastroom. - Stap 12
De seriële gegevens onderwerpen aan een 'run length codering' (compressieslag 5). - Stap 13
De omgezette gegevens comprimeren door middel van een 'entropie codering' op basis van het Huffmann algoritme (compressieslag 6).
Stap 1: het scannen
Het bronmateriaal zal in de meeste gevallen bestaan uit een ouderwetse analoge film. Er bestaan al decennia lang filmscanners die beeldje na beeldje omzetten in een digitaal beeld. Deze scanners werken met een resolutie van 720 bij 576 bij PAL-televisie en met 720 bij 480 bij het Amerikaanse NTSC-systeem. Dat wil zeggen dat ieder filmbeeld, zie de onderstaande figuur, in 576 lijnen wordt afgetast en dat er in iedere lijn 720 beeldmonstertjes worden genomen. Uit de aard van hun werking leveren scanners een 'RGB-schema' af. Ieder monster wordt ontleed in de drie basiskleuren rood, groen en blauw. Afhankelijk van de kleurverzadiging en de intensiteit wordt aan iedere basiskleur een code tussen '000' en '255' toegekend. Dat levert in totaal een kleurenspectrum van meer dan 16 miljoen kleuren op (true color). Op deze manier wordt het beeld omgezet in drie 'planes', een voor rood, een voor groen en een voor blauw.
 |
| Het omzetten van één frame van de analoge film in drie RGB-planes. (© 2019 Jos Verstraten) |
Het zou erg fraai zijn als de beelden verder verwerkt konden worden in die hoge resolutie van 720 bij 576. Dat kan helaas niet, de resulterende datastroom zou te groot zijn. Vandaar dat de resolutie wordt gereduceerd tot 352 bij 288. Dat gebeurt niet door eenvoudigweg ieder tweede pixel te laten wegvallen. In horizontale richting wordt een intelligent reductieschema toegepast, waarbij de elektronica gemiddelde kleurwaarden berekent van de pixels die behouden blijven en de pixels die worden verwijderd. In verticale richting kan een identiek proces worden toegepast, maar het is ook toelaatbaar dat simpelweg lijnen worden geschrapt.
Stap 3: RGB naar YUV vertaling
Een kleurenbeeld kan niet alleen volledig worden beschreven door de R-, G- en B- waarden. Het is ook mogelijk een beeld te definiëren door de luminantie Y en de chrominantie C. De eerste grootheid geeft informatie over de helderheid van het beeld, de tweede bepaalt de kleursamenstelling. Op een monochrome monitor wordt alleen de Y-waarde gebruikt. Om de kleur te omschrijven moet men wel twee grootheden voor de chrominantie definiëren. Deze worden Cu en Cv genoemd. Het grote voordeel van een definiëring volgens het YUV-schema is dat luminantie en chrominantie elkaar niet beïnvloeden en volledig afzonderlijk verwerkt kunnen worden. Het menselijke oog blijkt heel gevoelig voor variaties in de luminantie, maar veel minder gevoelig voor variaties in de chrominantie. Vandaar dat men kan volstaan met een kleinere resolutie bij het definiëren van de chrominantie. De verbanden tussen de R-, G- en B- waarden en de Y-, Cu- en Cv-waarden volgt uit de onderstaande transformatieformules:
Y = [0,299 ● R] + [0,587 ● G] + [0,114 ● B]
Cu = -[0,169 ● R] - [0,3316 ● G] + [0,5 ● B]
Cv = [0,5 ● R] - [0,4186 ● G] - [0,08l3 ● B]
Voor het omrekenen moet de processor van de coder dus slechts eenvoudige rekenkundige bewerkingen op de R-, G- en B-waarden uitvoeren, een fluitje van een cent. Er ontstaan nu drie nieuwe 'planes', waarbij de plane van Y nog steeds een resolutie van 352 bij 288 heeft. Omdat de informatie in de chrominantie niet zo belangrijk is, wordt de resolutie daarvan dramatisch verminderd. Er wordt een gemiddelde waarde berekent per vier pixels, volgens het schema van de onderstaande figuur. De kruisjes stellen de pixels van het gedigitaliseerde beeld voor. Van ieder pixel wordt eerst de luminantiewaarde berekend. Nadien worden de twee chrominatiewaarden van vier naast elkaar gelegen pixels berekend en wordt er de gemiddelde waarde van bepaald. Deze gemiddelde waarde wordt voorgesteld door de cirkeltjes. De planes van de twee C-waarden zijn door de reductie nu nog slechts 176 bij 144 pixels groot, alweer een aanzienlijke reductie waar de kwaliteit van het beeld nauwelijks door wordt beïnvloed!
 |
| Het reduceren van de chrominantie gegevens. (© 2019 Jos Verstraten) |
Voor de daaropvolgende ingewikkelde wiskundige bewerkingen zijn de volledige planes veel te groot. Deze worden ingedeeld in zogenaamde 'macroblokken' die slechts 8 bij 8 pixels groot zijn. De volledige definitie van een stukje beeld van 16 bij 16 pixels, op een standaard monitor goed voor ongeveer 120 vierkante millimeter beeldoppervlak, bestaat uit vier macroblokken voor de luminantie en twee macroblokken voor de chrominantie.
Stap 5: macroblokken opslaan in een geheugen
Vervolgens worden een heleboel van dergelijke macroblokken in een geheugen opgeslagen. Niet alleen alle macroblokken van het beeld dat verwerkt wordt, maar ook deze van enige voorgaande en volgende beelden.
Stap 6: motion compensation
Deze compressieslag vormt het hart van de MPEG technologie. Het filmbeeld bestaat uit 25 beeldjes per seconde. Nu zal het duidelijk zijn dat er in opeenvolgende filmbeeldjes veel identieke informatie zit. Stel als voorbeeld het filmfragment dat in de onderstaande figuur is voorgesteld. Een vrachtwagen rijdt van links onder naar rechts boven door het beeld. De achtergrond, bomen langs de weg, blijft hetzelfde. Het is dan overbodig om deze video-informatie in ieder beeld te gaan coderen door middel van de YUV-waarden. Dat kan in één beeld, in de volgende beelden wordt op de een of andere manier duidelijk gemaakt dat de informatie in de betreffende macroblokken ongewijzigd is gebleven. Ook de macroblokken die de vrachtwagen voorstellen veranderen inhoudelijk niet. Het enige verschil is dat de macroblokken in het beeld een andere positie innemen.
Het rechter beeld kan dus voor een groot deel samengesteld worden uit de macroblokken van het linker beeld. Natuurlijk zijn er ook elementen in het beeld die nieuw zijn. Daar waar in het linker beeld de vrachtwagen stond in nu een stuk weg plus omgeving te zien. Deze macroblokken bevatten dus beeldspecifieke informatie en moeten wél gecodeerd worden.
 |
| In deze twee frames zitten een heleboel identieke macroblokken. (© 2019 Jos Verstraten) |
Het principe van de reductie door middel van 'motion compensation' berust op twee grootheden: een verplaatsingsvector, 'motion vector' genoemd en een foutcorrectie, 'prediction error' genoemd. Deze begrippen worden toegelicht aan de hand van de onderstaande figuur. Stel dezelfde beeldvolgorde als in de illustratie van de rijdende vrachtwagen. Een macroblok dat een deel van de achterkant van de vrachtwagen voorstelt is verplaatst van de linker onderhoek van het beeld naar de rechter bovenhoek van het volgende beeld.
Die verplaatsing kan aangegeven worden door een verplaatsingsvector 'motion vector', het pijltje in de middelste figuur. Die vector kan gedefinieerd worden door slechts twee getallen: het eerste getal geeft de verplaatsing in horizontale richting weer, het tweede getal de verplaatsing in verticale richting. Die twee getallen nemen uiteraard heel wat minder ruimte in beslag dan de volledige YUV-codering van het 8 bij 8 pixels grote macroblok!
Nu kan het gebeuren dat er toch iets aan de inhoud van het verplaatste macroblok wijzigt. Stel bijvoorbeeld dat het macroblok niet een stuk vrachtwagen, maar een stuk van de jas van een bewegende man voorstelt. Door schaduwwerking en lichtinval zou het kunnen gebeuren dat de algemene kleurinvulling van het blok wel identiek is, maar dat er iets andere tinten aanwezig zijn. De hardware is in staat dat te detecteren en de 'prediction error' te berekenen. Dat zijn foutgegevens, die de YUV-gegevens van het blok in het linker beeld corrigeren naar de YUV-gegevens van het identieke blok in het rechter beeld. Maar deze foutcorrectie kan veel effectiever gecodeerd worden dan een volledige pixel na pixel beschrijving van het rechter macroblok.
Alweer een niet geringe datareductie!
In het getekende voorbeeld verandert er niets in de inhoud van het macroblok. De 'prediction error' (onderste figuur) bevat dus geen gegevens, hetgeen wordt voorgesteld door een codering met nullen. In een volgende compressieslag kunnen deze 64 nullen heel eenvoudig worden gecomprimeerd.
 |
| Het coderen van een macroblok door een motion vector en een prediction error. (© 2019 Jos Verstraten) |
Het zal duidelijk zijn dat het principe van motion vectors maar heel even werkt. Na een paar beeldjes is de vrachtwagen bijvoorbeeld volledig uit het beeld verdwenen en kan het systeem zich suf zoeken naar identieke macroblokken. Ook als een plotselinge beeldwisseling optreedt gaat het systeem de mist in. Dit probleem wordt opgevangen door regelmatig referentiebeelden op te nemen. Dat zijn beelden waarop geen compressie door middel van motion vectors en prediction errors wordt toegepast, maar die volledig worden beschreven door de YUV-waarden van al hun pixels.
Deze beelden worden 'I-frames' genoemd, de afkorting van 'Intra frame'. Als de scène rustig is worden er gemiddeld twee I-frames per seconde aangemaakt. Bij scènes met veel actie kan die frequentie echter behoorlijk oplopen. Uit één zo'n I-frame kunnen diverse 'P-frames' worden afgeleid. Dit proces noemt men 'forward prediction', het voorspellen van de inhoud van een beeld uit de gegevens van een vorig beeld. De 'P' van P-frame is uiteraard de afkorting van 'predicted', zo genoemd omdat de samenstelling van deze frames voor een groot deel uit de inhoud van het I-frame kan worden afgeleid.
Het berekenen van de motion vectors is echter voor zelfs de snelste processoren een immense klus. Zou men dat beeldje voor beeldje doen, dan zou het coderen van een film met MPEG-1 veel te veel tijd kosten. Vandaar worden er slechts om de drie beelden P-frames berekend. De tussenliggende beeldjes worden op een andere manier gecodeerd. Deze worden 'B-frames' genoemd, de afkorting van 'bidirectional'. Deze worden zo genoemd omdat zij worden gecodeerd door interpolatie van de gegevens uit I- en P-frames die links en rechts van het B-frame liggen. Dit proces wordt uiteraard 'bidirectional prediction' genoemd.

Een tussenstap: werking van forward en bidirectional prediction
Om nog eens terug te komen op het voorbeeld met de vrachtwagen, het zal duidelijk zijn dat het in de praktijk nooit voorkomt dat een vrachtwagen in één beeldovergang volledig door het beeld rijdt. Tussen de twee in de bovenstaande figuur getekende beeldjes liggen er een aantal, waarin de vrachtwagen steeds meer van links naar rechts en van onder naar boven opschuift. Als men nu het linker beeldje als I-frame codeert en het rechter beeldje als P-frame, dan kunnen de tussenliggende beelden gecodeerd worden door de horizontale en verticale waarden van de verplaatsingsvector van een macroblok te delen door het aantal tussenliggende beeldjes en nadien door middel van stapsgewijze vermeerdering de verplaatsingsvectoren van dat macroblok te coderen in de tussenliggende B-frames.
Dat scheelt een heleboel rekentijd voor de processor. Het algemene schema van de omzetting van de YUV-gecodeerde beeldjes in een IBP-codering is getekend in de onderstaande figuur. De pijltjes in deze tekening geven de richting aan waarin de processen van forward en bidirectional prediction verlopen.
 |
| Het omzetten van de normale YUV-beeldjes in opeenvolgende I-, B- en P-frames. (© 2019 Jos Verstraten) |
 |
| De volgorde van de I-, P- en B-frames in de seriële datastroom. (© 2019 Jos Verstraten) |
Het berekenen van alle 'motion vectors' is een ongelooflijk ingewikkelde opdracht voor de processor. In de meeste gevallen wordt volgens de volgende systematiek gewerkt. Vier naast elkaar liggende macroblokken uit een I-frame worden gecombineerd tot een 16 bij 16 pixelblok. Van dit blok worden een soort van gemiddelde waarden van de luminantie en de chrominantie berekend. Vervolgens wordt dit blok, zie de onderstaande figuur, geplaatst in een groter omliggend gedeelte van het P-frame dat 48 bij 48 pixels groot is.
De processor gaat nu in dat groter blok steeds opnieuw blokjes van 16 bij 16 onderzoeken op de gemiddelde waarden van luminantie en chrominantie. Als die waarden in het basisblok en het kandidaatblok ongeveer overeenstemmen, gaat het systeem er van uit dat het een identiek blok gevonden heeft in het P-frame en kan het de motion vector berekenen. Nu is het nauwelijks te geloven dat een dergelijk systeem in de praktijk werkt. Toch doet het dat bijna feilloos, wat mede te danken is een aan forse hap hogere wiskunde die wordt toegepast. In de praktijk worden de wiskundige wetten van de stochastiek, de waarschijnlijkheidsleer, uit de kast gehaald om de waarschijnlijke gelijkheid van blokken te beoordelen. Als u iets van dit soort wiskunde afweet zal het begrip 'gemiddelde kwadratische differentieelwaarde' u misschien iets zeggen!
 |
| Het zoeken naar gemiddelde waarden van luminantie en chrominantie. (© 2019 Jos Verstraten) |
In de vorige bewerking werd reeds een heleboel hogere wiskunde toegepast. Bij de DCT, 'discrete cosinus transformatie', worden de allerhoogste wiskundige registers open getrokken! DCT is een proces waarbij een tweedimensioneel continu amplitudeverloop kan omgezet worden in een ruimtelijk discreet frequentiespectrum. Dat zal u waarschijnlijk helemaal niets zeggen. Omdat DCT het absolute hart van MPEG en JPEG is, is het toch belangrijk dat dit proces begrijpelijk wordt gemaakt. Dat kan door een omweg te maken naar een begrip dat de meeste elektronici wél iets zal zeggen: de Fourier analyse.
Een tussenstap: Fourier analyse
In de onderstaande figuur is een periodiek analoog signaal voorgesteld. Dit signaal wordt in deze figuur beschreven door het verloop van zijn waarde (het amplitudeverloop) te tekenen in een assenstelsel, waarin de amplitude U(t) wordt uitgezet in functie van de tijd t. Dergelijke signalen zijn, hoe gek het ook klinkt, samengesteld uit niets meer dan een bepaalde gelijkspanning en verder een heleboel zuivere sinusoidale wisselspanningen met frequenties die gelijk zijn aan veelvouden van de eigen frequentie van het signaal. Iedere frequentie heeft een eigen grootte amplitude U(f) en de verhouding tussen deze groottes definieert volledig de vorm van het signaal.
Deze zuiver sinusvormige spanningen noemt men de 'harmonischen' van het signaal. Het signaal kan dus ook worden getekend onder de vorm van het frequentiespectrum dat onder in de illustratie is weergegeven. Dat is een lijndiagram, waarbij iedere lijn staat voor een harmonische. Deze worden gedefinieerd door hun frequentie op de horizontale frequentie as en door hun grootte op de verticale amplitude as. De ene gelijkspanning noemt men de DC-component van het signaal, alle sinusspanningen de AC-componenten. Het vreemde van de Fourier analyse is dat de grootte van de harmonischen afneemt naarmate hun frequentie stijgt. Dat heeft als gevolg dat die hoge harmonischen in feite niet erg veel bijdragen aan de vorm van het signaal. Als u bijvoorbeeld de signalen [8 ● f] tot en met [10 ● f] uit het signaal verwijdert, dan kunt u vast tellen dat het signaal er nauwelijks anders uitziet.
 |
| Een periodiek analoog signaal dat door de Fourier analyse kan omgezet worden in een frequentiespectrum. (© 2019 Jos Verstraten) |
Nu terug naar de discrete cosinus transformatie, maar even een recapitulatie. De beeldenstroom die werd aangevoerd als YUV-gecodeerde frames is in het vorig proces omgezet in een stroom van I-, B- en P-frames. Alleen de I-frames bevatten echte YUV-informatie, de B- en P-frames bevatten gecodeerde motion vectors en prediction error codes. De I-frames worden nu onderworpen aan een discrete cosinus transformatie. Dat geldt zowel voor de luminantie als voor de chrominantie gegevens.
Bekijk even de onderstaande figuur, de samenstelling van een macroblok uit een I-frame, dat de informatie over de luminantie van het blok bevat. Die informatie kunt u voorstellen door een matrix met 64 cellen waarbij iedere cel de luminantie waarde van het betreffende pixel bevat. Dat is een getal tussen '000' en '255'. In feite kan deze informatie ook ruimtelijk voorgesteld worden. Dit is getekend in het ruimtelijke diagram. Het grondvlak stelt de positie van de pixels uit het macroblok voor, de verticale as de waarde van de luminantie. De toppen van de staven vormen een glooiend patroon, op te vatten als een heuvelachtig landschap. De heuvels stellen het verloop van de luminantie voor in het macroblok.
 |
| De luminantie verdeling in een macroblok, onder de vorm van cijfers en onder de vorm van een amplitudeverloop voorgesteld. (© 2019 Jos Verstraten) |
Het gevolg van de DCT is dat er een nieuwe matrix ontstaat met nog steeds 64 getallen, zie de onderstaande figuur. Wat onmiddellijk opvalt is dat de meeste getallen in deze matrix veel kleiner zijn dan de getallen in de originele luminantie verdeling in het macroblok. Die getallen, die dus ieder de grootte van een harmonische geven, worden volgens een zigzag schema in de matrix geschreven, zie de onderstaande figuur rechts. In de linker bovenhoek staat het getal van de DC-component (1.260), rechts daarnaast de amplitude van de eerste harmonische (-1), links onder de amplitude van de tweede harmonisch (-23). Dat gaat al zigzaggend zo verder tot in de rechter benedenhoek de amplitude van de hoogste harmonische (0) wordt genoteerd.
De getallenmatrix in deze figuur kunt u niet meer interpreteren als het reële verloop van de luminantie over een beeldbereik van 8 bij 8 pixels. Het zijn 64 getallen, die op een volledig wiskundige manier het luminantieverloop beschrijven door aan te geven hoe het ruimtelijk frequentiespectrum van het macroblok er uit ziet. Let nog steeds op de overeenkomst met Fourier analyse van een elektrisch signaal!
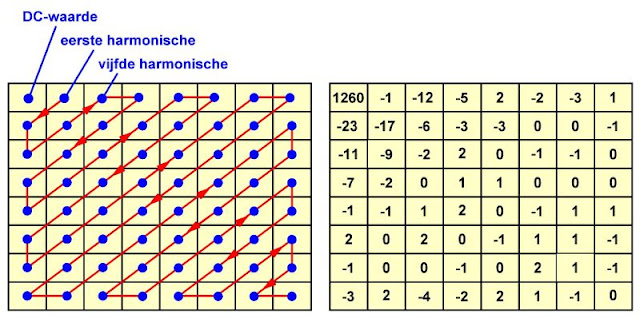 |
| De getallen matrix die ontstaat na de discrete cosinus transformatie. (© 2019 Jos Verstraten) |
De DCT-omzetting heeft als eerste groot voordeel dat het systeem minder gevoelig wordt voor fouten in de decodering. Stel dat de MPEG-decoder een heel foutieve waarde uit de seriële datastroom uitleest, bijvoorbeeld door een stoorpuls op de lijn. Zou men zonder meer luminantie- en chrominantiewaarden coderen, dan zou ieder foutief uitgelezen bit een felle lichtflits op het scherm tot gevolg kunnen hebben. Leest de MPEG-decoder echter een foutieve waarde van de DCT-matrix uit, dan zal dit alleen tot gevolg hebben dat het luminantieverloop over een gebied van 8 bij 8 pixels iets anders wordt. Dat valt veel minder op!
Het tweede groot voordeel van de DCT is dat, onderzoek de DCT-matrix van de bovenstaande figuur, er een heleboel hogere harmonischen zijn die een erg kleine amplitude hebben. Alweer vergelijkbaar met de Fourier analyse! In feite zit de belangrijkste beeldinformatie nu alleen in de linker bovenhoek van de matrix. Als al die kleine amplitudes van de hogere harmonischen op nul worden gesteld, zal dat nauwelijks gevolgen hebben voor het verloop van de luminantie in het macroblok. De DCT bereidt het systeem dus voor op een grote compressieslag, die in de volgende stap tot stand komt.
Stap 10: de psychovisuele quantisering van de DCT-matrix
Quantiseren is alweer een wiskundig begrip, dat simpelweg vertaald er op neer komt dat grote getallen worden omgezet in kleinere getallen door de grote getallen te delen door een bepaalde factor. Kleine getallen worden door deze deling tot nul gereduceerd. Als men dus de gegevens uit een DCT-matrix quantiseert, dan zullen er een heleboel nullen in de matrix ontstaan. Dit is de basis van de lossy compressie van JPEG.
DCT-waarden die door de quantisering worden gereduceerd tot nul kunnen namelijk nooit ofte nimmer worden herwonnen! Door het quantiseren gaan dus gegevens verloren en wordt de kwaliteit van het originele beeld aangetast. Het zal duidelijk zijn dat de compressiefactor afhankelijk is van de mate van quantisering. Neem als voorbeeld de DCT-matrix uit de vorige figuur. Als gequantiseerd wordt door alle DCT-waarden te delen door vier, dan blijven er na de deling nog maar tien waarden over die niet gelijk zijn aan nul. Alle overige DCT-waarden zijn namelijk kleiner dan vier en worden tot nul gereduceerd als zij door vier worden gedeeld. Quantiseert men echter door de matrix door te delen door acht, dan blijven er slechts zes waarden over die niet gelijk zijn aan nul. Het aantal nullen in de matrix neemt toe en daarmee de compressiefactor (zie verder), maar bij het herwinnen van de gegevens zal de DCT-matrix dus veel minder nauwkeurig worden gereconstrueerd dan bij quantisering door te delen door vier.
 |
| De 'psychovisuele quantiseringsmatrixen' voor de luminantie en chrominantie. (© 2019 Jos Verstraten) |
Na de quantisering van de Y-waarden van de DCT-matrix van het voorbeeld ontstaat de gequantiseerde matrix van de onderstaande figuur.
 |
| De DCT-matrix van het voorbeeld ná quantisering. (© 2019 Jos Verstraten) |
Men houdt dus rekening met de typische (on)gevoeligheid van het oog, vandaar dat men spreekt van 'psychovisuele' quantisering. Overigens is niemand verplicht zich aan deze quantiseringsfactoren te houden. Zoals reeds enige malen geschreven, MPEG-1 is een zeer open standaard waar iedereen die daar behoefte aan heeft eigen quantiseringsfactoren kan verzinnen. Wel moeten deze factoren dan natuurlijk mee met de datastroom verstuurd worden, zodat de elektronica van de decoder deze in een register kan inlezen en gebruiken om de gequantiseerde gegevens terug om te zetten in niet gequantiseerde DCT-waarden.
Een tussenstap: afrondingsfouten en de gevolgen daarvan
Bij dat herwinnen van gegevens heeft men te maken met een tweede afwijking. Het zal duidelijk zijn dat als men een DCT-waarde deelt door de quantiseringsfactor er zelden een resultaat zonder rest ontstaat. Deze rest wordt verwaarloosd, omdat steeds wordt afgerond naar gehele getallen. Als men nadien in de decoder de gequantiseerde waarden weer vermenigvuldigt met de quantiseringsfactoren, ontstaan in de meeste gevallen andere DCT-waarden dan de originele. In ons voorbeeld levert het quantiseren van de DC-component de waarde 79 op. Gaat de decoder dit getal weer vermenigvuldigen met de quantiseringsfactor 16, dan ontstaat een herwonnen DCT-waarde van 1.264 in plaats van de originele 1.260.
Ook deze afrondingsfouten dragen bij aan het lossy karakter van JPEG. Toch lijkt, ondanks al die vereenvoudigingen, weglatingen en fouten, het herwonnen beeld opmerkelijk goed op het oorspronkelijke beeld! Niet alleen een gevolg van de grote ongevoeligheid van het oog, maar ook van het feit dat DCT-waarden worden verwerkt, die niet pixelgewijs de inhoud van een macroblok bepalen, maar de algemene amplitude verdeling van luminantie en chrominantie in dat blok. Kleine afrondingsfouten beïnvloeden dan de 'heuvelachtigheid' van het amplitudeverloop van luminantie en chrominantie en hebben dan veel minder zichtbaar effect op het beeld. Het invoeren van de DCT was een gouden greep!
Stap 11: het vormen van de seriële datastroom
Na het quantiseren van de luminantie en chrominantie matrixen van alle macroblokken uit de I-frames worden deze gegevens weer in de reeds beschreven volgorde in de seriële datastroom opgenomen. De gegevens worden zigzaggend uit de matrixen van de macroblokken uitgelezen, zodat een seriële datastroom ontstaat. Het gevolg van deze zigzaggende uitlezing is dat er in de code vaak een heleboel nullen achter elkaar staan. Kijk maar naar ons besproken voorbeeld. Als de gegevens zigzaggend worden uitgelezen bestaat de seriële code van dit macroblok uit negen getallen die niet gelijk zijn aan nul en nadien uit 55 nullen. Met dergelijke gegevens kunnen compressie algoritmen wel overweg!
Stap 12: de run length codering
Een eerste stap bij het reduceren van al deze nullen is de zogenaamde 'run length codering'. Het principe is vrij eenvoudig en al een eeuwigheid in gebruik. Een data wordt voorgesteld door acht bits, onder de vorm van RRRR-SSSS. In de vier R-bits wordt het aantal data gecodeerd dat gelijk is aan nul en voor de te coderen data staat. In de S-bits wordt de waarde van de data binair gecodeerd.
In de onderstaande figuur is een voorbeeldje ter verduidelijking gegeven. De 'volgorde' geeft de seriële datastroom weer, de 'decimale code' de waarde van een data uit de stroom.
Data 001 heeft een waarde van 5. De codering van de R-bits is in dit voorbeeld onduidelijk omdat niet bekend is hoeveel nul-data vooraf gaan. De S-bits worden gecodeerd met '1010', de binaire representatie van het decimale getal '005'. Nadien volgen negen data die gelijk zijn aan nul. Deze worden niet gecodeerd. Het elfde data heeft '006' als decimale code. Omdat er negen '000'-data vooraf gaan, worden de R-bits gecodeerd met '1001', de binaire code voor 9. De S-bits worden gecodeerd als '0110', de binaire voorstelling van de decimale code '006'.
Dank zij deze codering worden de lange '000'-stromen heel efficiënt gecodeerd is slechts één byte, hetgeen een zeer grote datareductie oplevert.
De run length codering kent één uitzondering op de regel. Als na een data dat niet nul is alleen nog nul-data volgen, wordt het eerste nul-data gecodeerd met '0000-0000'. Omdat bekend is dat een macroblok uit 64 data bestaat kan de decoder uit deze ene code gemakkelijk afleiden dat de rest van de data van het macroblok alleen uit nul-data bestaat. De code '0000-0000' wordt 'EOB' genoemd, de afkorting van 'End Of Block'.
 |
| Een voorbeeld van de 'run length codering'. (© 2019 Jos Verstraten) |
In de laatste stap worden de run length bytes nog eens onderworpen aan een zogenaamde 'entropie codering' volgens het Huffmann algoritme. Huffmann was een Duitse wiskundestudent die als afstudeerproject de opdracht kreeg het meest efficiënte algoritme te ontwerpen om binaire gegevens te coderen. Dat deze man daarin meer dan geslaagd is mag blijken uit het feit dat het begrip 'Huffmann codering' een standaard is geworden in de data communicatie. Bij de Huffmann codering wordt een seriële datastroom onderzocht op het statistisch voorkomen van bepaalde codes. Codes die het vaakst aanwezig zijn worden nadien gecodeerd met slechts één bit. Codes die iets minder vaak aanwezig zijn worden gecodeerd met twee bits. De code die het minst aanwezig is wordt gecodeerd met de langste binaire code die het algoritme toelaat.
Een en ander wordt toegelicht aan de hand van de onderstaande figuur. De cijfers 0 tot en met 3 staan voor codes (eerste kolom). De hardware onderzoekt nu de procentuele aanwezigheid van deze codes in de datastroom. Code 1 is 45 % aanwezig, code 3 slechts 10 % (tweede kolom). De twee codes die het minst vaak voorkomen (0 en 3) krijgen nu de bits '0' en '1' toegewezen en worden nadien gecombineerd. Hun gezamenlijke aanwezigheid bedraagt 30 %, waardoor zij opschuiven naar de tweede plaats (derde kolom). Nu wordt aan de twee codes die het minst vaak voorkomen weer een '0' en '1' toegekend, nadien worden de codes weer verenigd, hetgeen in het getekend voorbeeld een voorkomen van 55 % oplevert. Deze code komt nu dus het vaakst voor, zodat zij oprukt naar de eerste plaats (vierde kolom). Ook nu wordt weer '0' en '1' toegekend.
 |
| Het Huffmann algoritme verklaard aan de hand van een eenvoudig voorbeeld. (© 2019 Jos Verstraten) |
Komt de hardware code 1 tegen, dan wordt deze gecodeerd door een enkelvoudig bit '0'. Daarbij maakt het niet uit hoe lang code 1 is! Komt het systeem code 2 tegen, dan wordt dit omgezet in de bitvolgorde '1-0'. In het getekende voorbeeld wordt code 3 omgezet in de langste bitcombinatie, namelijk '1-1-0'.
Het zal duidelijk zijn dat ook dit systeem een grote datareductie tot gevolg heeft. De RRRR- SSSS codes van de run length codering, ieder goed voor acht bit, worden via Huffmann omgezet in codes die gemiddeld genomen veel korter zijn.
In de onderstaande figuur is hiervan een voorbeeldje getekend.
 |
| Het omzetten van de run length codes in Huffmann codes. (© 2019 Jos Verstraten) |
De MPEG-1 codering van audio
Opmerking vooraf
Over het comprimeren van audio volgens de MPEG-standaard is op dit blog een eigen artikel gepubliceerd, lees Know-how: PASC audio-compressie.
Inleiding
MPEG-1 gebruikt voor het coderen van audio een algoritme dat in basis niet afwijkt van de 'PASC-codering' die onder andere Philips heeft ontwikkeld voor het MUSICAM-systeem. Er wordt dus gebruik gemaakt van 'perceptuele subbandcodering'. Het volledige audiospectrum wordt ingedeeld in 32 subbanden, op ieder band worden maskeringstechnieken toegepast om geluidsinformatie, die toch niet door het menselijk oor wordt opgevangen, te verwijderen.
Lagenconcept
Ook de audiocodering van MPEG-1 is een in te vullen standaard. De standaard schrijft de algemene principes voor, de gebruiker heeft een enorme vrijheid om eigen compressie algoritmen te definiëren en toe te passen. De standaard geeft ruimte aan drie zogenaamde 'layers' of lagen. Alle lagen kennen bemonsteringsfrequenties van 32 kHz, 44,1 kHz en 48 kHz en bieden vier werktoestanden:
- Monofoon geluid.
- Tweekanaals geluid.
- Stereofoon geluid.
- Joint stereo.
De laatste werktoestand zoekt de zogenoemde 'redundantie' oftewel identieke gegevens in beide stereokanalen op en verzendt deze informatie slechts éénmaal. Dit biedt ruimte in de beschikbare datastroom van ongeveer 200 kbit/s om het geluid met een hogere kwaliteit te versturen.
Layer 1
Laag 1 van MPEG-1 is het eenvoudigst opgezet. De specificaties voorzien in filtering naar 32 subbanden van gelijke bandbreedte, adaptieve bit toewijzing en blokcompressie op frames van 8 ms breedte. De resulterende datastroom kan ingesteld worden tussen 32 kbit/s en 448 kbit/s door het aanpassen van de compressie algoritmen. Layer 1 werd voornamelijk gedefinieerd voor goedkope consumententoepassingen, waarbij de noodzakelijke decodeer elektronica in één IC geïntegreerd kan worden.
Layer 2
Deze laag wordt ook wel 'MUSICAM' genoemd. Deze laag werkt met speciale compressietechnieken, waardoor de gegevensreductie toeneemt. Er wordt namelijk gecomprimeerd over veel langere frames. De noodzakelijke decodeerelektronica is echter ingewikkelder en dus duurder.
Layer 3
Deze laag biedt zeer goede specificaties, dank zij zeer uitgebreide en ingewikkelde compressie algoritmen. Bij deze laag wordt bijvoorbeeld gebruik gemaakt van Huffmann codering. Het gevolg is dat deze laag zelfs bij een monofone datastroom van slechts 64 kbit/s een zeer hoge geluidskwaliteit oplevert.
Geïntegreerde dynamiekcompressie
Zoals bekend wordt het meeste geluidsmaterieel begrensd in dynamisch bereik. Het dynamisch bereik geeft de verhouding tussen het 'stilste' geluid en het 'hardste' geluid in dB. Het toepassen van compressie is noodzakelijk om er zeker van te zijn dat de geluidsverwerkende apparatuur nooit overstuurd wordt. De audionormering van MPEG-1 biedt de mogelijkheid de compressiefactoren die in de studio worden bepaald mee te verzenden met de datastroom, zodat aan de ontvangerzijde de mogelijkheid bestaat de originele dynamiek van het geluid weer op een heel eenvoudige manier te herstellen.
Koop uw oscilloscoop bij Banggood
