
|
Kwantiseren betekent het omzetten van de waarde van een analoog signaal in een reeks digitale codes, waarvan het 'gewicht' recht evenredig is met de momentele waarde van het signaal.  |
Inleiding
Digitaal contra analoog
Het digitaal verwerken en bewerken van analoge elektronische signalen biedt een groot aantal voordelen. Op de eerste plaats kunt u het signaal, vanaf het moment dat het onder digitale vorm aanwezig is, onbeperkt verzenden en kopiëren zonder kwaliteitsverlies. Digitale codes hebben immers geen last van ruis en vervormingen, waar analoge verzend- en reproductiesystemen om berucht zijn. Op de tweede plaats kunt u op digitale codes ingewikkelde wiskundige algoritmes loslaten, waardoor het mogelijk is de gegevens op de meest vreemdsoortige manieren te bewerken. Zo kunt u, zuiver digitaal, het volledige audiospectrum van 20 Hz tot 20 kHz in zeer steile en smalle bandjes hakken en op ieder bandje allerlei signaalbewerkingen toepassen. Nadien kunt u, alweer zuiver digitaal, die smalle bandjes weer combineren tot het brede audiospectrum. Dergelijke technieken kunt u met de traditionele analoge schakelingen niet uitvoeren.
Transformaties die met analoge elektronische schakelingen niet of met veel moeite zijn uit te voeren, kunnen digitaal snel en met een grote nauwkeurigheid worden gerealiseerd. Het complexe rekenwerk wordt uiteraard razendsnel uitgevoerd door processoren.
Fysische verschijnselen zijn per definitie analoog
De meeste elektronische signalen zijn representanten van natuurkundige verschijnselen en zijn uiteraard geen digitale signalen, maar analoge. Neem als voorbeeld het geluid. Geluid ontstaat doordat de bron, bijvoorbeeld een muziekinstrument, de luchtmoleculen onder druk zet en nadien weer ontspant. Deze drukgolf plant zich voort door de moleculen van de lucht en brengt ergens anders het trommelvlies van een luisteraar aan het trillen. Maar door middel van een microfoon kunt u deze fysische verschijnselen heel nauwkeurig omzetten in elektrische wisselspanningen. Deze elektrische wisselspanningen zijn analoog. Dat wil zeggen dat de momentele waarde ervan iedere waarde kan hebben tussen een minimale en een maximale grootte. In de grafiek van de onderstaande figuur is boven een analoog signaal voorgesteld, zie de rode grafiek. Uit deze grafiek die het verloop van de spanning in functie van de tijd weergeeft, blijkt duidelijk dat dit signaal inderdaad iedere willekeurige waarde tussen twee grenzen kan aannemen.
 |
| Een analoog signaal (boven) wordt bemonsterd. (© 2020 Jos Verstraten) |
Het analoog signaal wordt omgezet in digitale codes. Dat doet u met behulp van een ADC, een 'analoog naar digitaal convertor'. Zo'n schakeling neemt op bepaalde tijden 'monsters' of 'samples' van het analoog signaal. De momentele analoge waarde van deze monsters wordt omgezet in een digitale code, waarvan de samenstelling een maat is voor de grootte van het analoog signaal op dat ene moment.
Bemonsteren of kwantiseren
Dit proces noemt men 'het bemonsteren van het analoog signaal' of het 'kwantiseren'. Dit proces wordt gestuurd door een kloksignaal, dat bepaalt hoeveel monsters er per seconde worden genomen.
Kwantiseren is een belangrijke techniek: foto's, muziek, en video worden tegenwoordig vrijwel uitsluitend digitaal verstuurd en verwerkt.
Van digitaal naar analoog
Als u de opgeslagen digitale monsters weer naar een analoog signaal wilt omzetten, moet u een DAC gebruiken, een 'digitaal naar analoog convertor'. Deze schakeling zet de digitale codes weer om in een analoog signaal.
Het basissysteem
Het basissysteem voor de digitale verwerking van analoge signalen is getekend in de onderstaande figuur. In dit voorbeeld wordt het systeem gebruikt voor het over een bepaalde tijd vertragen van het analoog signaal.
Dit ingangssignaal wordt door middel van een ADC omgezet in een aantal digitale codes Qa tot en met Qd. De momentele samenstelling van deze codes is een maat voor de momentele grootte van het analoog signaal. Aan de getekende samenstelling van deze codes moet u overigens geen waarde hechten, dit is maar een voorbeeld om het principe duidelijk te maken. Dat omzetten van het analoog signaal in digitale codes gebeurt uiteraard niet willekeurig, maar op regelmatige tijdsintervallen Δt. De digitale signalen (in dit simpele voorbeeld vier) worden nadien digitaal be- en/of verwerkt. In dit geval gaan de vier digitale signalen naar een digitale vertragingsschakeling. Als de gegevens weer beschikbaar moeten zijn, worden zij uit het digitale systeem gelezen op het ritme van dezelfde klok. De uitgangssignalen Qe tot en met Qh worden nu in een DAC weer omgezet in een analoog signaal. Dit uitgangssignaal noemt men het 'herwonnen analoog signaal'.
De kwantiseringsbenadering
Een digitaal signaal is per definitie een signaal dat maar twee waarden kan aannemen: 'L' of 'H'. Het zal dus duidelijk zijn dat ook een combinatie van een aantal digitale signalen maar een beperkt aantal combinaties van 'L' en 'H' kan bevatten.
Zet u een analoog signaal om in een digitale code, hoe ingewikkeld ook van samenstelling, dan zal die digitale code de momentele waarde van het analoog signaal alleen maar kunnen benaderen. Het oneindig aantal waarden van het analoog signaal wordt in een eindig aantal digitale codecombinaties ondergebracht.
Dit verschil tussen analoge en digitale signaalverwerking is een van de belangrijkste eigenschappen van ADC- en DAC-systemen. Dat wordt samengevat met het begrip 'kwantiseringsbenadering'. De uitgangscodes van een ADC zijn op ieder moment slechts een digitale benadering van het analoog ingangssignaal. Het zal dan ook wel duidelijk zijn dat, als deze benaderde codes weer via een DAC worden omgezet in het herwonnen analoog signaal, dit signaal ook een benadering zal zijn van het oorspronkelijke analoog signaal. Vandaar dat men zegt dat kwantisering altijd slechts een 'trapvormige benadering' van het originele analoog signaal levert. In de bovenstaande figuur is deze trapvormige benadering goed te zien en deze wordt nog eens, voor de duidelijkheid nogal overdreven voorgesteld, in de onderstaande figuur weergegeven. Uiteraard werkt men in de praktijk met meer dan vier digitale signalen en met meer monsters per seconde.
De kwantiseringsvervorming of -ruis
Tussen het originele analoog signaal en het herwonnen analoog signaal zal dus steeds een afwijking, een vervorming, bestaan. Deze vervorming kan wel geminimaliseerd worden, maar geheel verdwijnen zal deze nooit. Analoge signalen, die via ADC + DAC systemen weer in analoge signalen worden omgezet, worden dus per definitie vervormd! Deze principe-gebonden vervorming wordt de 'kwantiseringsvervorming' genoemd. Omdat deze vervorming zich in de praktijk meestal uit onder de vorm van kleine signaaltjes met een basisfrequentie gelijk aan deze van de klok spreekt men ook wel eens van de 'kwantiseringsruis'. De klok heeft immers een hoge frequentie en dergelijke hoge frequenties worden vaak ruis genoemd. Deze kwantiseringsruis is een van de belangrijkste specificaties van digitale signaalverwerkingssystemen en het minimaliseren van deze ruis is een van de grootste uitdagingen voor iedere elektronicus die zich bezig houdt met het ontwerpen van kwantiseringsschakelingen.

Een voorbeeld van de kwantiseringsruis
Als u een digitale oscilloscoop hebt merkt u deze kwantiseringsruis op vrijwel ieder plaatje dat u op het scherm zet. In de onderstaande foto ziet u hoe zo'n apparaat een zuivere sinusspanning weergeeft als u zowel de versterking als de tijdbasis flink opschroeft.
Overigens hebben vrijwel alle moderne digitale oscilloscopen een truukje aan boord om deze ruis te minimaliseren: 'Average Sampling'.
De woordlengte
De woordlengte definieert het aantal bits dat wordt gebruikt voor het omzetten van het analoog signaal in een digitale code. Werkt u met een systeem met zestien bits (een vaak gebruikte standaard) dan spreekt men van een woordlengte van 16 bit. Het zal wel zonder toelichting duidelijk zijn dat de kwantiseringsruis daalt naarmate u meer bits gebruikt. Vandaar dat de beeldkwaliteit van een tien bit digitale scope veel beter is dan deze van een acht bit soortgenoot.
De resolutie
De resolutie van een ADC geeft aan in hoeveel 'kwantiseringszones' u het analoog signaal na digitalisatie kunt onderbrengen. Het zal duidelijk zijn dat een systeem met een woordlengte van 1 bit een resolutie heeft van 2. U kunt de resolutie berekenen door het cijfer 2 te verheffen tot de macht van het aantal bits. Een systeem met een woordlengte van 16 bit heeft dus een resolutie van 216 = 65.536. Met een dergelijk systeem kunt u de momentele waarde van een analoog signaal onderbrengen in 65.536 kwantiseringszones.
Het dynamisch bereik
Het dynamisch bereik geeft de logaritmische verhouding weer tussen de minimale en de maximale signaalverandering die een DAC in het herwonnen analoog signaal kan veroorzaken. De maximale verandering ontstaat als alle bits opeens omschakelen van 'L' naar 'H'. De minimale verandering ontstaat als alleen het LSB omschakelt van 'L' naar 'H'. Het zal duidelijk zijn dat het dynamisch bereik toeneemt naarmate er meer bits bij de omzetting betrokken zijn. Hoe groter de woordlengte, hoe groter het dynamisch bereik! Het dynamisch bereik wordt uitgedrukt in dB en wordt ook wel eens de signaal/ruis-verhouding van het systeem genoemd.
De bitgrootte
De bitgrootte geeft aan met hoeveel volt het met een DAC terug gewonnen analoog signaal varieert als het LSB van 'L' naar 'H' springt. De bitgrootte en het dynamisch bereik zijn dus in feite twee grootheden die hetzelfde fysische verschijnsel beschrijven. Maar terwijl het dynamisch bereik een verhouding weergeeft en onafhankelijk is van de maximale grootte van de terug te winnen spanning, is het alleen zinvol de bitgrootte op te geven als u weet wat de maximale spanning is die uit een DAC kan komen. Vaak noemt men de bitwaarde van het systeem 'de LSB van het systeem'.
Verband tussen woordlengte, resolutie, dynamisch bereik en bitwaarde
Het zal logisch zijn dat er tussen de vier besproken basisgrootheden van ieder kwantiseringssysteem een oorzakelijk verband bestaat. Dit verband is in de tabel van de onderstaande figuur gegeven voor woordlengtes van 1 tot en met 16 bit. De opgegeven bitgroottes gaan uit van een analoge spanning met een maximale waarde van 10 V.
De sample-frequentie
Het digitaliseren van een analoog signaal is geen continu proces, maar een proces dat gestuurd wordt door een externe klokpuls. De frequentie van dit kloksignaal noemt men de 'sample-frequentie'. Deze frequentie bepaalt dus hoeveel samples er per seconde van de analoge ingangsspanning worden genomen en hoeveel verschillende digitale codes er op de uitgang van de ADC per seconde zullen ontstaan. De eenheid van deze grootheid is dan ook samples per seconde, voorgesteld door Sa/sec. Omdat tegenwoordig vaak wordt gewerkt met sample-frequenties die in het MHz-bereik liggen wordt de eenheid vaak voorgesteld door MSa/s of zelfs GSa/s, miljoen of miljard samples per seconde.
Het gewicht van de bits en het MSB en LSB
In het onderstaande voorbeeld is een zaagtandvormig stijgende analoge spanning getekend met een maximale waarde van 15 V. Deze wordt gekwantificeerd door middel van een ADC met vier bits. Deze schakeling levert de standaard binaire code. De kloksnelheid is gelijk aan zestien keer de snelheid van de zaagtand. In de tabel ziet u de samenstelling van de vier bits bij iedere klokpuls. Wat hierbij opvalt is dat het bit Qa van waarde verandert bij iedere volt stijging van de zaagtand. Bit Qb verandert van waarde na iedere 2 V stijging van de zaagtand. Het vierde bit Qd verandert slechts één keer van waarde en wel bij een zaagtandspanning van 8 V. Het is dus mogelijk aan ieder bit een bepaald 'gewicht' toe te kennen. Bit Qa is het 'lichtst', bit Qd het 'zwaarst'. Een waardeverandering van Qa komt immers slechts overeen met een analoge spanningsverandering van 1 V. De waardeverandering van Qd kont echter overeen met een analoge waardeverandering van 8 V.
Vandaar dat men het bit Qa het 'Least Significant Bit' noemt, afgekort tot 'LSB' en het bit Qd het 'Most Significant Bit', afgekort tot 'MSB'.
De minimale sample-frequentie is belangrijk
Een belangrijke vraag is hoeveel monsters u per seconde moet nemen. Het zal wel duidelijk zijn dat de kwaliteit van het systeem verbetert naarmate u meer monsters per seconde neemt. Maar meer samples per seconde betekent hogere frequenties voor de klok, dus ingewikkelder en duurdere elektronica. Vandaar dat men alleen geïnteresseerd is in de vraag hoe weinig monsters men moet nemen om er toch zeker van te zijn dat het herwonnen analoog signaal lijkt op het ingangssignaal van de ADC.
Een voorbeeld uit de praktijk
Uit een zwarte doos komt een onbekend signaal. De vraag is hoe dit signaal er uit ziet. Als u een digitale oscilloscoop op de uitgang aansluit en een hoge tijdbasis van 8 ns/div kiest ziet het signaal uit zoals voorgesteld in oscillogram-1 in de onderstaande foto. De zwarte doos levert dus blijkbaar een sinus met een frequentie van 24 MHz. Als u nu echter de tijdbasis trager maakt, bijvoorbeeld tot 4 μs/div, krijgt u een geheel ander plaatje op het scherm, zie oscillogram-2. Het lijkt alsof er allerlei onregelmatigheden in het signaal aanwezig zijn. Natuurlijk wilt u dit verschijnsel beter bekijken, dus u bevriest oscillogram-2 op het scherm en verbreedt het beeld tot 80 ns/div. Nu ziet u oscillogram-3 op uw scherm. De vraag is welk signaal de zwarte doos levert, dat van oscillogram-1 of dat van oscillogram-3.
Wat is het verschil? De twee eerste beelden zijn met hetzelfde aantal samples per seconde genomen. Bij het tweede beeld worden er echter veel meer perioden van het signaal op het scherm weergegeven dan bij het eerste beeld. Per periode worden er dus veel minder monsters genomen dan bij beeld 1. Als u nu beeld 2 gaat uitrekken tot er maar enige tientalen periodes op het scherm verschijnen ziet u dat door het beperkt aantal samples per periode er een volledig foutief beeld van de werkelijkheid kan ontstaan.
Het sampling theorema
U kunt blijkbaar niet grenzeloos verder gaan met het reduceren van de sampling-frequentie. Wiskundig kunt u berekenen dat de sampling-frequentie minstens twee maal zo groot moet zijn als de hoogste frequentie in het analoog signaal. Deze algemene zeer belangrijke wet staat bekend als het 'sampling theorema'. Theorema is een geleerd woord voor het bekende begrip stelling.
Sampelt u met een lagere frequentie, dan is het absoluut onmogelijk om de vorm van het analoog signaal uit de opeenvolgende digitale samples terug te winnen. Het experiment met de digitale oscilloscoop was daar een mooi voorbeeld van!

Het sampling theorema grafisch aangetoond
Hoewel het in het kader van dit artikel te ver zou gaan om dit wiskundig bewijs te leveren, kan men dit effect ook heel dramatisch grafisch aantonen. In de onderstaande figuur wordt een sinusvormige analoge spanning met een frequentie van 15 kHz gesampeld met een klokfrequentie die steeds kleiner wordt. Als u nadien de opeenvolgende digitale codes met een DAC omzet in een analoge spanning ontstaat een signaal dat een benadering van het sinussignaal zou moeten zijn.
Dat klopt nog vrij aardig als u sampled met een frequentie van 7,5 kHz. Maar naarmate de sample-frequentie steeds lager wordt zal het herwonnen analoog signaal steeds minder op de originele sinus gaan lijken. Bij zeer lage sample-frequenties is het herwonnen signaal zelfs niet eens meer als sinus herkenbaar, maar wordt het een driehoek meteen veel lagere frequentie.
Iets dergelijks gebeurde ook bij het bemonsteren van het signaal uit de zwarte doos.
Alias-frequentie en -vervorming
Deze veel lagere frequentie noemt men de 'alias-frequentie' en de grote vervorming die in dit geval ontstaat bij het kwantiseren de 'alias-vervorming'. Kans op alias-vervorming is steeds aanwezig als u bemonstert met een frequentie die lager is dan 2 x de hoogste signaalfrequentie. Als u een ingangssignaal hebt met bekende frequentie kunt u deze alias-vervorming vermijden door de sample-frequentie minstens twee maal hoger te kiezen.
Een aansprekend voorbeeld uit films
Een heel bekend voorbeeld van alias-vervorming is het verschijnsel dat in een film de wielen van een voertuig soms achteruit lijken te draaien. De spaken van de wielen bewegen dan in de analoge werkelijkheid te snel voor de digitale bemonstering door de filmcamera (24 beelden per seconde) waardoor deze alias-fout optreedt.
Harry Nyquist en de Nyquist-frequentie
Harry Nyquist toonde wiskundig aan dat dergelijke fouten niet kunnen optreden als de bemonsteringsfrequentie groter is dan tweemaal de hoogste frequentie-component in het te bemonsteren signaal. Deze frequentie wordt de 'Nyquist-frequentie' genoemd. Als u een signaal bemonstert moet u door middel van een laagdoorlaat filter er voor zorgen dat alle frequenties die hoger zijn dan de helft van de Nyquist-frequentie worden weggefilterd. Alleen dan loopt u geen risico op het ontstaan van alias-vervorming.
Bij een audio-CD wordt bijvoorbeeld bemonsterd met een klokfrequentie van 44,1 kHz. Deze Nyquist-frequentie is twee keer hoger dan de hoogst hoorbare frequentie in het geluidssignaal. Om alias-vervorming te voorkomen zorgt een analoog filter ervoor dat alle frequenties boven 22,05 kHz vóór de kwantisering van het geluid dusdanig worden verzwakt dat ze niet meer van invloed zijn.
Hiervoor is een scherp afsnijdend laagdoorlaat filter noodzakelijk.
Meer dan alleen een ADC!
Aan de hand van de tot nu toe verzamelde wetenschap kunt u beredeneren wat er komt kijken als u een analoog signaal in een digitale code wilt omzetten. Het fundamentele blokschema van een dergelijk systeem is getekend in de onderstaande figuur.
Het te digitaliseren signaal wordt eerst door het anti-alias filter gevoerd en gaat vervolgens naar de een zogenaamde 'sample and hold' (S&H). De uitgang van deze schakeling gaat naar de analoge ingang van de ADC. De S&H en de ADC worden gestuurd door een extern kloksignaal dat de sample-frequentie vastlegt.
Het laagdoorlaat filter
Dit filter moet een zeer scherp afsnijdend filter zijn, dat de maximale frequentie van het te kwantiseren signaal onverzwakt doorlaat, maar twee maal die frequentie met tientallen dB's verzwakt. U ontkomt dan niet aan het gebruik van derde of zelfs vijfde orde actieve filters.
Over dergelijke schakelingen is op dit blog een uitgebreid artikel verschenen, lees Schakelingen: laagdoorlaat filters.
De noodzaak van een externe klok
De ADC werkt niet continu. Als u de digitale code op de uitgang continu laat aanpassen aan de veranderingen van het analoog ingangssignaal, dan kan er een echte code-chaos ontstaan op de uitgang van de ADC. Het omzetten van de analoge signalen in een digitale code is een proces dat namelijk niet traagheidsloos verloopt. Iedere ADC heeft een bepaalde conversie-tijd die in het μs-bereik ligt. Bovendien zal het ene bit iets sneller reageren dan het andere. Als u zonder externe regie de analoge spanning continu in digitale codes zou omzetten, dan zou het systeem de digitale code per ongeluk kunnen uitlezen op het moment dat een of meerdere bits bezig zijn zich aan de nieuwe analoge ingangssituatie aan te passen. De code kan op dat moment volledig foute informatie bevatten.
Om deze problemen te voorkomen moet u werken met een externe klok. Dat wil zeggen dat u op regelmatige tijdsintervallen een monstertje neemt van de momentele waarde van het ingangssignaal, dit monstertje even opslaat in een analoog geheugen en nadien dit monster omzet in de bijbehorende digitale code. Dan hebt u geen last van de beschreven verschijnselen omdat de waarde van het monster constant blijft. Nadat de conversie-tijd van de ADC verstreken is kunt u de digitale code uitlezen en verder verwerken. Nadien kan een nieuw monster worden genomen en kunt u het proces herhalen.
De sample and hold
Het analoge geheugen, waarin het monster van het analoge signaal even wordt bewaard, wordt steeds uitgevoerd onder de vorm van een 'sample and hold', afgekort tot S&H. Het basisprincipe van een S&H is getekend in de onderstaande figuur. Het analoog signaal wordt aangeboden aan een buffer A1. De uitgang van de buffer gaat via een elektronische schakelaar, uitgevoerd onder de vorm van een FET T1, naar een tweede buffer A2. Tussen de ingang van deze buffer en de massa staat een condensator C1 geschakeld. Als u de elektronische schakelaar open stuurt, zal de condensator zich opladen tot de momentele waarde van de analoge ingangsspanning. Omdat de waarde van de condensator zeer klein is, zal het geen probleem zijn om de condensatorspanning de variatie op de ingangsspanning traagheidsloos te laten volgen. Opent u de elektronische schakelaar, dan wordt de verbinding tussen de uitgang van de eerste buffer en de ingang van de tweede buffer verbroken. Het gevolg is dat de condensatorspanning niet kan afvloeien en constant blijft. Uiteraard zal er wel iets lading weglekken via de zeer hoge ingangsimpedantie van de tweede buffer en via allerlei lekweerstanden in de schakeling. Maar omdat het bemonsteren redelijk snel gaat kunt u er op vertrouwen dat gedurende de sample-tijd de spanning over de condensator gelijk blijft aan de momentele waarde van het ingangssignaal op het moment dat de schakelaar geopend werd.
Nu kunt u de ADC opdracht geven de waarde van de spanning op de uitgang van de S&H te kwantiseren. Op het moment dat de code op de uitgangen van de ADC stabiel is kunt u deze uitlezen en een tweede cyclus starten.
(Banggood sponsor advertentie)
Koop uw multimeter bij Banggood

Van digitaal naar analoog
Als u de opgeslagen digitale monsters weer naar een analoog signaal wilt omzetten, moet u een DAC gebruiken, een 'digitaal naar analoog convertor'. Deze schakeling zet de digitale codes weer om in een analoog signaal.
Het basissysteem
Het basissysteem voor de digitale verwerking van analoge signalen is getekend in de onderstaande figuur. In dit voorbeeld wordt het systeem gebruikt voor het over een bepaalde tijd vertragen van het analoog signaal.
Dit ingangssignaal wordt door middel van een ADC omgezet in een aantal digitale codes Qa tot en met Qd. De momentele samenstelling van deze codes is een maat voor de momentele grootte van het analoog signaal. Aan de getekende samenstelling van deze codes moet u overigens geen waarde hechten, dit is maar een voorbeeld om het principe duidelijk te maken. Dat omzetten van het analoog signaal in digitale codes gebeurt uiteraard niet willekeurig, maar op regelmatige tijdsintervallen Δt. De digitale signalen (in dit simpele voorbeeld vier) worden nadien digitaal be- en/of verwerkt. In dit geval gaan de vier digitale signalen naar een digitale vertragingsschakeling. Als de gegevens weer beschikbaar moeten zijn, worden zij uit het digitale systeem gelezen op het ritme van dezelfde klok. De uitgangssignalen Qe tot en met Qh worden nu in een DAC weer omgezet in een analoog signaal. Dit uitgangssignaal noemt men het 'herwonnen analoog signaal'.
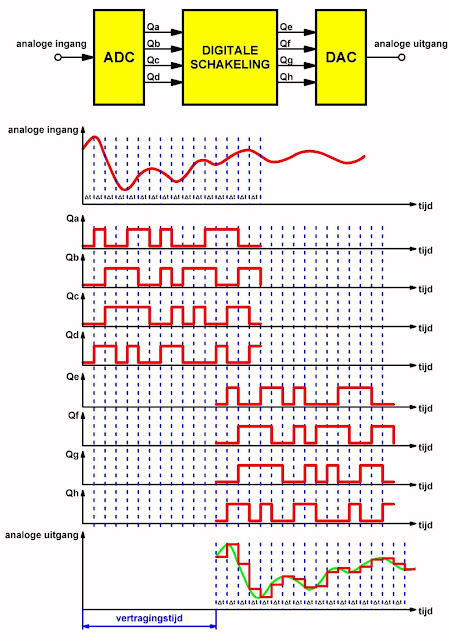 |
| Het basissysteem voor het digitaal verwerken van een analoog signaal. (© 2020 Jos Verstraten) |
Een digitaal signaal is per definitie een signaal dat maar twee waarden kan aannemen: 'L' of 'H'. Het zal dus duidelijk zijn dat ook een combinatie van een aantal digitale signalen maar een beperkt aantal combinaties van 'L' en 'H' kan bevatten.
Zet u een analoog signaal om in een digitale code, hoe ingewikkeld ook van samenstelling, dan zal die digitale code de momentele waarde van het analoog signaal alleen maar kunnen benaderen. Het oneindig aantal waarden van het analoog signaal wordt in een eindig aantal digitale codecombinaties ondergebracht.
Dit verschil tussen analoge en digitale signaalverwerking is een van de belangrijkste eigenschappen van ADC- en DAC-systemen. Dat wordt samengevat met het begrip 'kwantiseringsbenadering'. De uitgangscodes van een ADC zijn op ieder moment slechts een digitale benadering van het analoog ingangssignaal. Het zal dan ook wel duidelijk zijn dat, als deze benaderde codes weer via een DAC worden omgezet in het herwonnen analoog signaal, dit signaal ook een benadering zal zijn van het oorspronkelijke analoog signaal. Vandaar dat men zegt dat kwantisering altijd slechts een 'trapvormige benadering' van het originele analoog signaal levert. In de bovenstaande figuur is deze trapvormige benadering goed te zien en deze wordt nog eens, voor de duidelijkheid nogal overdreven voorgesteld, in de onderstaande figuur weergegeven. Uiteraard werkt men in de praktijk met meer dan vier digitale signalen en met meer monsters per seconde.
 |
| De trapvormige benadering is een basiseigenschap van kwantisering. (© 2020 Jos Verstraten) |
Tussen het originele analoog signaal en het herwonnen analoog signaal zal dus steeds een afwijking, een vervorming, bestaan. Deze vervorming kan wel geminimaliseerd worden, maar geheel verdwijnen zal deze nooit. Analoge signalen, die via ADC + DAC systemen weer in analoge signalen worden omgezet, worden dus per definitie vervormd! Deze principe-gebonden vervorming wordt de 'kwantiseringsvervorming' genoemd. Omdat deze vervorming zich in de praktijk meestal uit onder de vorm van kleine signaaltjes met een basisfrequentie gelijk aan deze van de klok spreekt men ook wel eens van de 'kwantiseringsruis'. De klok heeft immers een hoge frequentie en dergelijke hoge frequenties worden vaak ruis genoemd. Deze kwantiseringsruis is een van de belangrijkste specificaties van digitale signaalverwerkingssystemen en het minimaliseren van deze ruis is een van de grootste uitdagingen voor iedere elektronicus die zich bezig houdt met het ontwerpen van kwantiseringsschakelingen.

Een voorbeeld van de kwantiseringsruis
Als u een digitale oscilloscoop hebt merkt u deze kwantiseringsruis op vrijwel ieder plaatje dat u op het scherm zet. In de onderstaande foto ziet u hoe zo'n apparaat een zuivere sinusspanning weergeeft als u zowel de versterking als de tijdbasis flink opschroeft.
Overigens hebben vrijwel alle moderne digitale oscilloscopen een truukje aan boord om deze ruis te minimaliseren: 'Average Sampling'.
 |
| De kwantiseringsruis van een digitale oscilloscoop. (© 2020 Jos Verstraten) |
De specificaties van kwantiseringssystemen
De woordlengte
De woordlengte definieert het aantal bits dat wordt gebruikt voor het omzetten van het analoog signaal in een digitale code. Werkt u met een systeem met zestien bits (een vaak gebruikte standaard) dan spreekt men van een woordlengte van 16 bit. Het zal wel zonder toelichting duidelijk zijn dat de kwantiseringsruis daalt naarmate u meer bits gebruikt. Vandaar dat de beeldkwaliteit van een tien bit digitale scope veel beter is dan deze van een acht bit soortgenoot.
De resolutie
De resolutie van een ADC geeft aan in hoeveel 'kwantiseringszones' u het analoog signaal na digitalisatie kunt onderbrengen. Het zal duidelijk zijn dat een systeem met een woordlengte van 1 bit een resolutie heeft van 2. U kunt de resolutie berekenen door het cijfer 2 te verheffen tot de macht van het aantal bits. Een systeem met een woordlengte van 16 bit heeft dus een resolutie van 216 = 65.536. Met een dergelijk systeem kunt u de momentele waarde van een analoog signaal onderbrengen in 65.536 kwantiseringszones.
Het dynamisch bereik
Het dynamisch bereik geeft de logaritmische verhouding weer tussen de minimale en de maximale signaalverandering die een DAC in het herwonnen analoog signaal kan veroorzaken. De maximale verandering ontstaat als alle bits opeens omschakelen van 'L' naar 'H'. De minimale verandering ontstaat als alleen het LSB omschakelt van 'L' naar 'H'. Het zal duidelijk zijn dat het dynamisch bereik toeneemt naarmate er meer bits bij de omzetting betrokken zijn. Hoe groter de woordlengte, hoe groter het dynamisch bereik! Het dynamisch bereik wordt uitgedrukt in dB en wordt ook wel eens de signaal/ruis-verhouding van het systeem genoemd.
De bitgrootte
De bitgrootte geeft aan met hoeveel volt het met een DAC terug gewonnen analoog signaal varieert als het LSB van 'L' naar 'H' springt. De bitgrootte en het dynamisch bereik zijn dus in feite twee grootheden die hetzelfde fysische verschijnsel beschrijven. Maar terwijl het dynamisch bereik een verhouding weergeeft en onafhankelijk is van de maximale grootte van de terug te winnen spanning, is het alleen zinvol de bitgrootte op te geven als u weet wat de maximale spanning is die uit een DAC kan komen. Vaak noemt men de bitwaarde van het systeem 'de LSB van het systeem'.
Verband tussen woordlengte, resolutie, dynamisch bereik en bitwaarde
Het zal logisch zijn dat er tussen de vier besproken basisgrootheden van ieder kwantiseringssysteem een oorzakelijk verband bestaat. Dit verband is in de tabel van de onderstaande figuur gegeven voor woordlengtes van 1 tot en met 16 bit. De opgegeven bitgroottes gaan uit van een analoge spanning met een maximale waarde van 10 V.
 |
| De voornaamste specificaties samengevat. (© 2020 Jos Verstraten) |
Het digitaliseren van een analoog signaal is geen continu proces, maar een proces dat gestuurd wordt door een externe klokpuls. De frequentie van dit kloksignaal noemt men de 'sample-frequentie'. Deze frequentie bepaalt dus hoeveel samples er per seconde van de analoge ingangsspanning worden genomen en hoeveel verschillende digitale codes er op de uitgang van de ADC per seconde zullen ontstaan. De eenheid van deze grootheid is dan ook samples per seconde, voorgesteld door Sa/sec. Omdat tegenwoordig vaak wordt gewerkt met sample-frequenties die in het MHz-bereik liggen wordt de eenheid vaak voorgesteld door MSa/s of zelfs GSa/s, miljoen of miljard samples per seconde.
Het gewicht van de bits en het MSB en LSB
In het onderstaande voorbeeld is een zaagtandvormig stijgende analoge spanning getekend met een maximale waarde van 15 V. Deze wordt gekwantificeerd door middel van een ADC met vier bits. Deze schakeling levert de standaard binaire code. De kloksnelheid is gelijk aan zestien keer de snelheid van de zaagtand. In de tabel ziet u de samenstelling van de vier bits bij iedere klokpuls. Wat hierbij opvalt is dat het bit Qa van waarde verandert bij iedere volt stijging van de zaagtand. Bit Qb verandert van waarde na iedere 2 V stijging van de zaagtand. Het vierde bit Qd verandert slechts één keer van waarde en wel bij een zaagtandspanning van 8 V. Het is dus mogelijk aan ieder bit een bepaald 'gewicht' toe te kennen. Bit Qa is het 'lichtst', bit Qd het 'zwaarst'. Een waardeverandering van Qa komt immers slechts overeen met een analoge spanningsverandering van 1 V. De waardeverandering van Qd kont echter overeen met een analoge waardeverandering van 8 V.
Vandaar dat men het bit Qa het 'Least Significant Bit' noemt, afgekort tot 'LSB' en het bit Qd het 'Most Significant Bit', afgekort tot 'MSB'.
 |
| Verklaring van de begrippen LSB en MSB. (© 2020 Jos Verstraten) |
Het sampling theorema
De minimale sample-frequentie is belangrijk
Een belangrijke vraag is hoeveel monsters u per seconde moet nemen. Het zal wel duidelijk zijn dat de kwaliteit van het systeem verbetert naarmate u meer monsters per seconde neemt. Maar meer samples per seconde betekent hogere frequenties voor de klok, dus ingewikkelder en duurdere elektronica. Vandaar dat men alleen geïnteresseerd is in de vraag hoe weinig monsters men moet nemen om er toch zeker van te zijn dat het herwonnen analoog signaal lijkt op het ingangssignaal van de ADC.
Een voorbeeld uit de praktijk
Uit een zwarte doos komt een onbekend signaal. De vraag is hoe dit signaal er uit ziet. Als u een digitale oscilloscoop op de uitgang aansluit en een hoge tijdbasis van 8 ns/div kiest ziet het signaal uit zoals voorgesteld in oscillogram-1 in de onderstaande foto. De zwarte doos levert dus blijkbaar een sinus met een frequentie van 24 MHz. Als u nu echter de tijdbasis trager maakt, bijvoorbeeld tot 4 μs/div, krijgt u een geheel ander plaatje op het scherm, zie oscillogram-2. Het lijkt alsof er allerlei onregelmatigheden in het signaal aanwezig zijn. Natuurlijk wilt u dit verschijnsel beter bekijken, dus u bevriest oscillogram-2 op het scherm en verbreedt het beeld tot 80 ns/div. Nu ziet u oscillogram-3 op uw scherm. De vraag is welk signaal de zwarte doos levert, dat van oscillogram-1 of dat van oscillogram-3.
Wat is het verschil? De twee eerste beelden zijn met hetzelfde aantal samples per seconde genomen. Bij het tweede beeld worden er echter veel meer perioden van het signaal op het scherm weergegeven dan bij het eerste beeld. Per periode worden er dus veel minder monsters genomen dan bij beeld 1. Als u nu beeld 2 gaat uitrekken tot er maar enige tientalen periodes op het scherm verschijnen ziet u dat door het beperkt aantal samples per periode er een volledig foutief beeld van de werkelijkheid kan ontstaan.
 |
| Het sampling theorema in de praktijk. (© 2020 Jos Verstraten) |
U kunt blijkbaar niet grenzeloos verder gaan met het reduceren van de sampling-frequentie. Wiskundig kunt u berekenen dat de sampling-frequentie minstens twee maal zo groot moet zijn als de hoogste frequentie in het analoog signaal. Deze algemene zeer belangrijke wet staat bekend als het 'sampling theorema'. Theorema is een geleerd woord voor het bekende begrip stelling.
Sampelt u met een lagere frequentie, dan is het absoluut onmogelijk om de vorm van het analoog signaal uit de opeenvolgende digitale samples terug te winnen. Het experiment met de digitale oscilloscoop was daar een mooi voorbeeld van!

Het sampling theorema grafisch aangetoond
Hoewel het in het kader van dit artikel te ver zou gaan om dit wiskundig bewijs te leveren, kan men dit effect ook heel dramatisch grafisch aantonen. In de onderstaande figuur wordt een sinusvormige analoge spanning met een frequentie van 15 kHz gesampeld met een klokfrequentie die steeds kleiner wordt. Als u nadien de opeenvolgende digitale codes met een DAC omzet in een analoge spanning ontstaat een signaal dat een benadering van het sinussignaal zou moeten zijn.
Dat klopt nog vrij aardig als u sampled met een frequentie van 7,5 kHz. Maar naarmate de sample-frequentie steeds lager wordt zal het herwonnen analoog signaal steeds minder op de originele sinus gaan lijken. Bij zeer lage sample-frequenties is het herwonnen signaal zelfs niet eens meer als sinus herkenbaar, maar wordt het een driehoek meteen veel lagere frequentie.
Iets dergelijks gebeurde ook bij het bemonsteren van het signaal uit de zwarte doos.
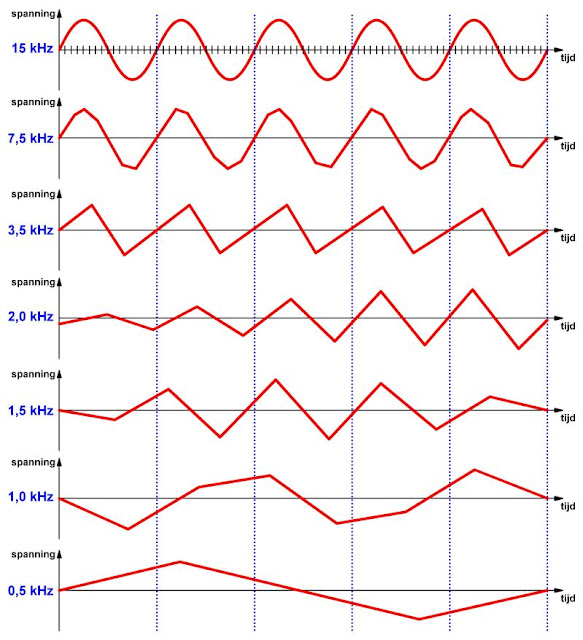 |
| Het sampling theorema grafisch toegelicht. (© 2020 Jos Verstraten) |
Deze veel lagere frequentie noemt men de 'alias-frequentie' en de grote vervorming die in dit geval ontstaat bij het kwantiseren de 'alias-vervorming'. Kans op alias-vervorming is steeds aanwezig als u bemonstert met een frequentie die lager is dan 2 x de hoogste signaalfrequentie. Als u een ingangssignaal hebt met bekende frequentie kunt u deze alias-vervorming vermijden door de sample-frequentie minstens twee maal hoger te kiezen.
Een aansprekend voorbeeld uit films
Een heel bekend voorbeeld van alias-vervorming is het verschijnsel dat in een film de wielen van een voertuig soms achteruit lijken te draaien. De spaken van de wielen bewegen dan in de analoge werkelijkheid te snel voor de digitale bemonstering door de filmcamera (24 beelden per seconde) waardoor deze alias-fout optreedt.
Harry Nyquist en de Nyquist-frequentie
Harry Nyquist toonde wiskundig aan dat dergelijke fouten niet kunnen optreden als de bemonsteringsfrequentie groter is dan tweemaal de hoogste frequentie-component in het te bemonsteren signaal. Deze frequentie wordt de 'Nyquist-frequentie' genoemd. Als u een signaal bemonstert moet u door middel van een laagdoorlaat filter er voor zorgen dat alle frequenties die hoger zijn dan de helft van de Nyquist-frequentie worden weggefilterd. Alleen dan loopt u geen risico op het ontstaan van alias-vervorming.
Bij een audio-CD wordt bijvoorbeeld bemonsterd met een klokfrequentie van 44,1 kHz. Deze Nyquist-frequentie is twee keer hoger dan de hoogst hoorbare frequentie in het geluidssignaal. Om alias-vervorming te voorkomen zorgt een analoog filter ervoor dat alle frequenties boven 22,05 kHz vóór de kwantisering van het geluid dusdanig worden verzwakt dat ze niet meer van invloed zijn.
Hiervoor is een scherp afsnijdend laagdoorlaat filter noodzakelijk.
Blokschema voor het kwantiseren van analoge signalen
Meer dan alleen een ADC!
Aan de hand van de tot nu toe verzamelde wetenschap kunt u beredeneren wat er komt kijken als u een analoog signaal in een digitale code wilt omzetten. Het fundamentele blokschema van een dergelijk systeem is getekend in de onderstaande figuur.
Het te digitaliseren signaal wordt eerst door het anti-alias filter gevoerd en gaat vervolgens naar de een zogenaamde 'sample and hold' (S&H). De uitgang van deze schakeling gaat naar de analoge ingang van de ADC. De S&H en de ADC worden gestuurd door een extern kloksignaal dat de sample-frequentie vastlegt.
 |
| Het blokschema van een kwantiseringsschakeling. (© 2020 Jos Verstraten) |
Dit filter moet een zeer scherp afsnijdend filter zijn, dat de maximale frequentie van het te kwantiseren signaal onverzwakt doorlaat, maar twee maal die frequentie met tientallen dB's verzwakt. U ontkomt dan niet aan het gebruik van derde of zelfs vijfde orde actieve filters.
Over dergelijke schakelingen is op dit blog een uitgebreid artikel verschenen, lees Schakelingen: laagdoorlaat filters.
De noodzaak van een externe klok
De ADC werkt niet continu. Als u de digitale code op de uitgang continu laat aanpassen aan de veranderingen van het analoog ingangssignaal, dan kan er een echte code-chaos ontstaan op de uitgang van de ADC. Het omzetten van de analoge signalen in een digitale code is een proces dat namelijk niet traagheidsloos verloopt. Iedere ADC heeft een bepaalde conversie-tijd die in het μs-bereik ligt. Bovendien zal het ene bit iets sneller reageren dan het andere. Als u zonder externe regie de analoge spanning continu in digitale codes zou omzetten, dan zou het systeem de digitale code per ongeluk kunnen uitlezen op het moment dat een of meerdere bits bezig zijn zich aan de nieuwe analoge ingangssituatie aan te passen. De code kan op dat moment volledig foute informatie bevatten.
Om deze problemen te voorkomen moet u werken met een externe klok. Dat wil zeggen dat u op regelmatige tijdsintervallen een monstertje neemt van de momentele waarde van het ingangssignaal, dit monstertje even opslaat in een analoog geheugen en nadien dit monster omzet in de bijbehorende digitale code. Dan hebt u geen last van de beschreven verschijnselen omdat de waarde van het monster constant blijft. Nadat de conversie-tijd van de ADC verstreken is kunt u de digitale code uitlezen en verder verwerken. Nadien kan een nieuw monster worden genomen en kunt u het proces herhalen.
De sample and hold
Het analoge geheugen, waarin het monster van het analoge signaal even wordt bewaard, wordt steeds uitgevoerd onder de vorm van een 'sample and hold', afgekort tot S&H. Het basisprincipe van een S&H is getekend in de onderstaande figuur. Het analoog signaal wordt aangeboden aan een buffer A1. De uitgang van de buffer gaat via een elektronische schakelaar, uitgevoerd onder de vorm van een FET T1, naar een tweede buffer A2. Tussen de ingang van deze buffer en de massa staat een condensator C1 geschakeld. Als u de elektronische schakelaar open stuurt, zal de condensator zich opladen tot de momentele waarde van de analoge ingangsspanning. Omdat de waarde van de condensator zeer klein is, zal het geen probleem zijn om de condensatorspanning de variatie op de ingangsspanning traagheidsloos te laten volgen. Opent u de elektronische schakelaar, dan wordt de verbinding tussen de uitgang van de eerste buffer en de ingang van de tweede buffer verbroken. Het gevolg is dat de condensatorspanning niet kan afvloeien en constant blijft. Uiteraard zal er wel iets lading weglekken via de zeer hoge ingangsimpedantie van de tweede buffer en via allerlei lekweerstanden in de schakeling. Maar omdat het bemonsteren redelijk snel gaat kunt u er op vertrouwen dat gedurende de sample-tijd de spanning over de condensator gelijk blijft aan de momentele waarde van het ingangssignaal op het moment dat de schakelaar geopend werd.
Nu kunt u de ADC opdracht geven de waarde van de spanning op de uitgang van de S&H te kwantiseren. Op het moment dat de code op de uitgangen van de ADC stabiel is kunt u deze uitlezen en een tweede cyclus starten.
 |
| Het basisschema van een sample and hold. (© 2020 Jos Verstraten) |
Koop uw multimeter bij Banggood
