
|
Na weerstanden zijn condensatoren de vaakst toegepaste passieve componenten in de elektronica. In twee artikelen geven wij een overzicht van de belangrijkste toepassingen van dit onderdeel.

|
Inleidende begrippen over de condensator
Condensatoren parallel en in serie schakelen
U kunt, net zoals weerstanden, condensatoren parallel of in serie schakelen. De formules voor het berekenen van de vervangingswaarde zijn echter precies omgekeerd als bij weerstanden. Dus: als u condensatoren parallel schakelt, dan wordt de totale waarde groter dan de grootste waarde van de deelcondensatoren. Als u condensatoren in serie schakelt, dan wordt de totale waarde kleiner dan de kleinste waarde van de aan de schakeling deelnemende onderdelen.
Voor een parallel schakeling van een aantal condensatoren, zoals getekend in de onderstaande figuur links, ziet de formule er als volgt uit:
Ctotaal = C1 + C2 + C3
Met andere woorden, u moet gewoon de waarden in farad bij elkaar optellen.
Als de volgende condensatoren in parallel geschakeld worden:
C1 = 1.000 pF
C2 = 2.200 pF
C3 = 3.300 pF
dan is de totale condensator gelijk aan:
Ctotaal = 1.000 pF + 2.200 pF + 3.300 pF
Ctotaal = 6.500 pF
Voor een serieschakeling van condensatoren, zoals getekend in de figuur rechts, is de formule:
1 / Ctotaal = [1 / C1] + [1 / C2] + [1 / C3]
Als u, zoals in de praktijk meestal zal voorkomen, slechts twee condensatoren in serie schakelt, dan kunt u de algemene formule vereenvoudigen tot:
Ctotaal = [C1 • C2] / [C1 + C2]
U deelt dus het product van de waarde van de twee condensatoren door de som van hun waarde.
Meestal zal men in de praktijk alleen maar even grote condensatoren in serie schakelen. Daar heeft men goede redenen voor, zoals uit een van de volgende paragrafen zal volgen. De formule wordt dan heel wat handzamer. De totale capaciteit is dan gelijk aan de capaciteit van de afzonderlijke condensatoren, gedeeld door het aantal in serie geschakelde exemplaren. Als u drie condensatoren van 3.300 μF in serie schakelt wordt de vervangende capaciteit Ctotaal 1.100 μF.
 |
| In serie en parallel schakelen van condensatoren. (© 2024 Jos Verstraten) |
Het verhogen van de werkspanning
Stel dat u een condensator van 1 µF nodig hebt met een werkspanning van 600 V. Zo'n condensator blijkt nergens te koop. Wat gedaan? De onderstaande figuur brengt de zeer eenvoudige oplossing. U schakelt enige condensatoren met een lagere werkspanning in serie, en overbrugt iedere condensator met een zeer grote weerstand. Natuurlijk moet de waarde van de condensatoren aangepast worden. Deze wordt gelijk aan de gewenste waarde vermenigvuldigd met het aantal in serie geschakelde condensatoren. In het getekende voorbeeld wordt dat dus 3 x 1 µF is gelijk aan 3 µF. Deze waarde is geen bestaande, zodat u moet afronden naar 3,3 µF.
Wat is het nut van de parallel geschakelde weerstanden? Condensatoren zijn, in theorie, perfecte isolatoren voor gelijkspanning. Maar een ideale isolator bestaat in de praktijk niet. Een condensator heeft dus toch een weerstand, hoewel die met normale middelen niet eens meetbaar is. Als u de drie condensatoren zonder meer in serie schakelt zal de totale 600 V zich over de condensatoren verdelen, evenredig met hun 'lekweerstand' (zo noemt men de niet gewenste weerstand van een isolator). Als een van de drie nu wat meer weerstand heeft dan de overige twee zal het grootste gedeelte van de 600 V toch nog over die ene condensator komen te staan, wat natuurlijk niet de bedoeling is.
Vandaar dat men aanraadt zeer grote weerstanden over de condensatoren te schakelen. De waarde van 10 MΩ is zeer klein, vergeleken met de lekweerstanden van de condensatoren, maar groot genoeg om de schakeling, waarin de condensatoren opgenomen worden, niet te beïnvloeden. De 600 V ziet nu drie even grote lekweerstanden van ongeveer 10 MΩ en zal zich netjes over de drie condensatoren verdelen.
 |
| Verhogen van de werkspanning van een condensator. (© 2024 Jos Verstraten) |
Het maken van een bipolaire elco
Grote condensatorwaarden zijn alleen beschikbaar als elco (electrolytische condensator) en een elco is gepolariseerd. Het onderdeel heeft een positieve en een negatieve aansluiting en u mag zo'n condensator nooit op een wisselspanning aansluiten. Tóch hebt u af en toe een grote, ongepolariseerde condensator nodig. Denk bijvoorbeeld aan scheidingsfilters in luidsprekerboxen, waar grote condensatoren noodzakelijk zijn voor het sturen van de lage frequenties naar de woofer-luidspreker. Hoe u die kunt maken met twee diodes en twee elco's is geschetst in onderstaande figuur. In het rood is aangegeven hoe de stroom door de schakeling van plus naar min loopt. U ziet dat de elco die de verkeerde polariteit heeft wordt overbrugd door een geleidende diode. Het resultaat is een condensator die u zonder problemen op een wisselspanning kunt aansluiten.
 |
| Het maken van een bipolaire elco. (© 2024 Jos Verstraten) |
Toepassingen van condensatoren
Condensatoren worden zo vaak gebruikt, dat zelfs de voornaamste toepassingen niet in één artikel aan de orde kunnen komen. Vandaar dat wij dit verhaal splitsen in twee artikelen. In dit eerste artikel worden de onderstaande fundamentele toepassingen van een condensator behandeld:
1 - De condensator, aangesloten op gelijkspanning
2 - De condensator als tijdbepalend element
3 - De condensator als afvlakker van voedingsspanning
4 - De condensator als integrator en differentiator
5 - De condensator als koppel-element
6 - De condensator, aangesloten op wisselspanning
7 - De condensator als terugkoppel element
In het tweede artikel, dat u kunt lezen via:
Aanklikbare link ➡ Know-how: condensator toepassingen (deel 2)
worden de onderstaande toepassingen van condensatoren besproken:
8 - De condensator als bootstrap element
9 - De condensator in toonregelingen
10 - De condensator in actieve filters
11 - De condensator in afgestemde kringen
12 - De condensator in oscillatoren
1 - De condensator, aangesloten op gelijkspanning
Inleiding
Uit de definitie van wat een condensator is, twee geleiders gescheiden door een isolator, zal duidelijk zijn dat zo'n onderdeel geen gelijkspanning doorlaat. Als u dan ook met een op weerstand geschakelde ouderwetse analoge multimeter tussen de klemmen van een condensator meet, zult u vaststellen dat de naald van de meter op oneindig blijft staan. Of bewoog de naald toch heel even? Goed gezien, want als u een condensator aansluit op een gelijkspanning gebeuren er vreemde dingen. Er vloeit bijvoorbeeld heel even een stroompje door het onderdeel. Dat stroompje is verantwoordelijk voor het even naar links gaan van de naald van de meter. Aan de hand van de onderstaande figuur kunt u verklaren wat er gebeurt. In deze figuur is een serieschakeling getekend opgebouwd uit een batterij B1, een omschakelaar S1, een weerstand R1 en een condensator C1. Door middel van de omschakelaar kunt u de combinatie C1-R1 ofwel verbinden met de batterij, ofwel kortsluiten.
Als de schakelaar in stand 'b' staat zijn weerstand en condensator kortgesloten en meet u natuurlijk geen spanning over de condensator. Dat is in de grafiek voorgesteld door het vette horizontale lijntje, dat samenvalt met de horizontale tijd-as. Als u de schakelaar op een bepaaId moment t1 omschakelt naar de stand 'a' wordt de R-C combinatie met de batterij verbonden. Meet nu de spanning UC1 over de condensator om de seconde en zet die spanningen uit in een grafiek in functie van de tijd. U zult merken dat de spanning over de condensator zal stijgen van nul tot de waarde van de batterijspanning. De snelheid van deze spanningsstijging hangt af van de grootte van de condensator en van de waarde van de weerstand. Dit verschijnsel noemt men het opladen van een condensator.
 |
| Het laden en ontladen van een condensator. (© 2024 Jos Verstraten) |
Het laden van de condensator
Hoe is dit verschijnsel te verklaren? Op het moment t1 dat u de schakelaar S1 van stand 'b' naar stand 'a' verplaatst staat de linker aansluiting van de weerstand op de batterijspanning UB1 en de rechter aansluiting op de condensatorspanning UC1. Deze is echter nul, er staat de maximale spanning over de weerstand. De stroom I door de weerstand is maximaal. De stroom zal lading in de condensator pompen. Het gevolg is dat er spanning over de condensator wordt opgebouwd. De rechter aansluiting van de weerstand komt dus op een hogere spanning te staan. De spanningsval over de weerstand daalt, de stroom door de weerstand zal dus ook dalen. De kleinere stroom heeft weer tot gevolg dat de lading minder snel in de condensator wordt gepompt. De spanning over de condensator stijgt minder snel. Dit proces gaat door tot de spanning over de condensator gelijk wordt aan de batterijspanning. Er staat dan geen spanning over de weerstand, de stroom wordt nul.
Bij het laden van de condensator vloeit de stroom I van links naar rechts door de weerstand.
In een situatie met praktische waarden voor R1 en C1 gebeurt dat laden van de condensator in minder dan één seconde. Vandaar dat de naald van de analoge multimeter even uitslaat als u de weerstand van de condensator meet. Dat is de reactie van de meter op het even vloeien van de laadstroom.
Het ontladen van de condensator
Als u vervolgens de schakelaar S1 op tijdstip t2 weer van stand 'a' naar stand 'b' verplaatst wordt de linker aansluiting van de weerstand opeens aangesloten op een spanning van 0 V. De rechter staat op de spanning over de opgeladen condensator. De spanning over de weerstand is maximaal en er gaat weer een grote stroom I door dit onderdeel vloeien, maar nu van rechts naar links. Door het vloeien van die stroom wordt er lading uit de condensator gepompt, de spanning over dit onderdeel gaat dalen. De spanningsval over de weerstand wordt dus kleiner, de stroom I daalt. Na een bepaalde tijd is alle lading uit de condensator afgevloeid. De spanning over de condensator is nul, over de weerstand staat geen spanning en de stroom I wordt ook nul.

De tijdconstante 𝜏 van een RC-kring
Uit de vorige paragraaf volgt dat de grootte van de laad- en de ontlaadstroom bepaald wordt door de waarde van de weerstand in de keten. Naast deze weerstand speelt natuurlijk ook de grootte van de condensator een rol. Immers, hoe groter de capaciteit van de condensator, hoe meer ruimte er is om lading in op te slaan en hoe langer het zal duren voor de spanning over de condensator gelijk is aan de spanning van de batterij.
Met andere woorden: de laadtijd van de condensator is zowel afhankelijk van de grootte van de condensator als van de waarde van de weerstand. Beide onderdelen zijn recht evenredig met de laadtijd. Als u de weerstand vergroot zal ook laadtijd langer worden. Stijgt de waarde van de condensator, dan heeft dit hetzelfde gevolg op de laadtijd.
Deze onderlinge relatie tussen de laadtijd, de waarde van de weerstand en de grootte van de condensator heeft men uitgedrukt in het begrip 'tijdconstante'. Deze grootheid wordt voorgesteld door de Griekse letter 𝜏. De tijdconstante is het product van de weerstand in ohm en de condensator in farad en wordt uitgedrukt in seconde. Dus:
𝜏 = R1 • C1
Als in de keten van de vorige figuur een weerstand van 1 Ω en een condensator van 1 F zouden staan, dan zou de tijdconstante 𝜏 van die kring 1 s zijn.
Maar hierdoor is nog niet duidelijk wat de definitie van die tijdconstante is. Wel, de tijdconstante is de tijd, die de condensator in de kring nodig heeft om op te laden tot 63,2 % van de batterijspanning of om te ontladen tot 36,8 % van zijn laadspanning. De laad- en ontlaadcurven van een R-C netwerk, zoals getekend in de vorige figuur, zijn nog eens wat duidelijker getekend in de onderstaande figuur. Hieruit blijkt duidelijk dat de spanning over de condensator niet lineair toe- of afneemt. De stijging of daling van de spanning over het onderdeel is in het begin van de laad- of ontlaadcyclus groter dan op het einde.
Dat is een zeer belangrijk gegeven, dat in heel wat schakelingen van pas komt, maar af en toe erg vervelende consequenties heeft.
 |
| Het begrip 'tijdconstante' ingevuld in de laad- en ontlaadcurve. (© 2024 Jos Verstraten) |
Asymptotische lading en ontlading
Hoe vreemd het ook lijkt, wiskundig kan men aantonen dat de spanning over de ladende condensator nooit helemaal gelijk wordt aan de batterijspanning! Het laden verloopt 'asymptotisch', hetgeen wil zeggen dat de spanning over de condensator de batterijspanning wel steeds meer zal benaderen, maar nooit precies er aan gelijk wordt. In de praktijk echter kunt u aannemen dat de spanning over de condensator na vijf maal de tijdconstante zo goed als gelijk is aan de gelijkspanning van de bron.
Hetzelfde verhaal geldt voor de ontlading. Ook bij dit proces kan wiskundig worden bewezen dat de ontladende condensator alleen in het oneindige volledig ontladen zal zijn. Maar ook nu kunt u rustig stellen dat na vijf keer de tijdconstante de condensator 'leeg' is.
2 - De condensator als tijdbepalend element
Inleiding
Uit de besproken theorie van het laden en opladen van een condensator kunt u een belangrijke conclusie trekken. Een condensator heeft er enige tijd voor nodig om zichzelf op te laden of te ontladen tot de spanning, waarop hij wordt aangesloten. Dat gegeven wordt in iedere elektronische schakeling, waarin de tijd een rol speelt, gebruikt. Als u een schakeling moet ontworpen die bijvoorbeeld een korte spanningspuls op de uitgang opwekt, dan kunt u er zeker van zijn dat de tijdsduur van die spanningspuls bepaald wordt door een RC-kring.
Eerste voorbeeld: pulsgenerator rond een schmitt-trigger
In de onderstaande figuur is een mooi voorbeeld gegeven van een schakeling die het laden en ontladen van een condensator via een weerstand nuttig gebruikt. Gebruik wordt gemaakt van een schmitt-trigger poort, zoals de 74LS13. De schmitt-trigger poort wordt geschakeld als astabiele multivibrator. De vier ingangen worden met elkaar verbonden. Deze punten gaan enerzijds via een condensator C naar de massa en anderzijds via een weerstand R naar de uitgang.
De werking berust op het gegeven dat een schmitt-trigger een zogenaamde 'hysteresis' heeft. De schakeling werkt als inverterende poort. Als u de ingangsspanning Uin van 0 V laat stijgen zal de uitgang Uuit 'H' zijn totdat de spanning op de ingang een bepaalde drempel U2 overschrijdt. Deze spanning wordt gezien als 'H', het gevolg is dat de uitgang 'L' wordt. Als u nadien de ingangsspanning weer laat dalen, blijft de uitgang 'L' totdat een tweede kleinere drempel U1 wordt bereikt. Op dat moment klapt de poort om en de uitgang wordt weer 'H'. Het spanningsverschil tussen de twee drempels noemt men de 'hysteresis' van de schakeling.
De twee externe onderdelen R en C vormen de laad- en ontlaadkring. Als de uitgang 'H' is, zal de condensator door de weerstand worden opgeladen. De condensatorspanning kan stijgen tot de bovenste drempel U2. Op dat moment klapt de schakeling om. De uitgang wordt 'L' met als gevolg dat de condensator nu gaat ontladen via de weerstand. De condensatorspanning gaat dalen totdat de onderste drempel U1 wordt bereikt. De uitgang wordt nu weer 'H', het proces gaat zich nu herhalen.
Op de uitgang van de poort verschijnt dus een blokvormig signaal, dat heen en weer slingert tussen de massa 'L' en de normale hoge uitgangsspanning 'H' van de poort. De frequentie van dit signaal wordt bepaald door de waarde van de tijdconstante R • C. Hoe hoger R en C, hoe lager de frequentie.
 |
| Een RC laad- en ontlaadkring in een pulsgenerator. (© 2024 Jos Verstraten) |
Tweede voorbeeld: pulsgenerator rond een 555 timer
Als tweede voorbeeld bespreken wij een schakeling rond het bekende timer-IC 555. De frequentie van deze pulsgenerator wordt bepaald door de waarde van de onderdelen R1, R2, R3 en C2. De drie genoemde weerstanden laden de condensator op uit de voedingsspanning. De werking wordt verklaard aan de hand van de rechter grafieken in de onderstaande figuur. In de 555 zijn twee comparatoren (spanningsvergelijkers) aanwezig die de spanning over de condensator vergelijken met ⅓ en ⅔ van de voedingsspanning.
Als de spanning over de condensator gelijk wordt aan ⅔ van de voedingsspanning klapt één van de comparatoren om. Pen 7 van de 555 wordt dan intern met de massa verbonden en de condensator wordt nu heel snel via de zeer kleine weerstand R3 ontladen tot ⅓ van de voedingsspanning. De tweede interne comparator klapt om, pen 7 gaat weer naar een hoge impedantie toestand en de condensator wordt weer opgeladen via de weerstanden R1, R2 en R3. De uitgang van de 555 op pen 3 is hoog als de condensator wordt geladen en wordt intern naar de massa getrokken als de condensator wordt ontladen. Er ontstaan zeer smalle negatief gerichte pulsjes die via weerstand R5 aan de basis van een PNP-transistor T1 worden aangeboden. Deze gaat geleiden bij zo'n smal pulsje. Punt D, de uitgang van de schakeling, wordt positief gedurende de pulstijd van de 555.
Derde voorbeeld: pulsgenerator rond een op-amp
De schakeling is opgebouwd rond een operationele versterker van het type 741. Dit IC werkt als astabiele rechthoekgolf multivibrator. Dat is een gevolg van de dubbele terugkoppeling van de uitgang naar de twee ingangen. De inverterende ingang is aangesloten op het knooppunt van de terugkoppeling R3/C1. De niet-inverterende ingang is verbonden met het knooppunt van de terugkoppeling R2/R1.
Wat deze twee terugkoppelingen voor invloed hebben blijkt uit de grafieken van onderstaande figuur. Stel dat twee batterijen van +4,5 V en -4,5 V worden aangesloten als voeding + en -. De condensator C1 is ontladen, de inverterende ingang staat dus op 0 V. Stel verder dat de uitgang op een positieve spanning U++ staat. Deze spanning wordt teruggekoppeld naar de niet-inverterende ingang, zodat dit punt op een positieve spanning U1 staat, die kleiner is dan U++. Het blijkt nu dat de stelling klopt! Omdat de niet-inverterende ingang positiever is dan de inverterende, zal de uitgang van de op-amp vastlopen tegen de positieve voedingsspanning, dus inderdaad op U++ staan!
De condensator C1 gaat zich via weerstand R3 opladen uit de spanning U++. De spanning op de inverterende ingang gaat dus langzaam stijgen. Op tijdstip t1 wordt deze spanning iets groter dan U1. De inverterende ingang wordt nu positiever dan de niet-inverterende ingang. Het gevolg is dat de op-amp omklapt. De uitgang loopt vast tegen de negatieve voedingsspanning en wordt opeens gelijk aan U--. Ook deze spanning wordt via R2/R1 teruggekoppeld naar de niet-inverterende ingang, zodat deze op een spanning U2 komt te staan. U2 is in absolute waarde even groot als U1.
De condensator C1 gaat nu ontladen naar de negatieve uitgangsspanning U--. Op tijdstip t3 wordt deze ingang iets negatiever dan de niet-inverterende ingang. De schakeling klapt weer om, het proces herhaalt zich.
Op de uitgang ontstaat dus een rechthoekgolf, waarvan de frequentie wordt bepaald door de laad- en ontlaadtijd van de condensator en door de waarde van de spanningen U1 en U2.
 |
| Een pulsgenerator rond een 741 op-amp. (© 2024 Jos Verstraten) |
3 - De condensator als afvlakker van voedingsspanning
Iedere schakeling heeft minstens eén voedingsspanning nodig
Of een schakeling gebruik maakt van een traditionele voeding met trafo en gelijkrichter of van een moderne geschakelde voeding, aan de uitgang van de voeding zult u steeds een grote condensator aantreffen die tot taak heeft de geleverde spanning om te vormen tot een zo mooi mogelijke gelijkspanning. Dit wordt 'afvlakken' genoemd, de condensator heet de 'afvlakcondensator'. De noodzakelijke waarde van de condensator is zo groot dat hiervoor altijd een elco wordt toegepast. U zult in voedingen elco's aantreffen van 470 μF tot wel 10.000 μF.
Omdat in moderne gecompliceerde schakelingen soms wel vier voedingsspanningen noodzakelijk zijn zult u, als u een modern elektronisch apparaat open schroeft, onmiddellijk de grote elco's opmerken die in de voeding zitten.
 |
| Grote afvlakcondensatoren op een voedingsprint. (© Amazon) |
Afvlakken bij een traditionele voeding
In de onderstaande figuur is de meest eenvoudige uitvoering van een traditionele voeding getekend. De halve periode gelijkrichter bestaat uit een nettrafo met één secundaire wikkeling, een diode D1, een afvlakcondensator C1 en een belastingsweerstand R1.
Wat gebeurt er bij het inschakelen van deze voeding? Tijdens de eerste positieve halve periode van de secundaire trafospanning geleidt de diode en staat de trafo-spanning over de weerstand en de ongeladen condensator. De condensator laadt zich op tot de trafo-spanning (eerste rood deel van de curve in de tekening). Als de trafospanning weer gaat dalen, gaat de diode sperren. Over de weerstand staat dan de laadspanning van de condensator (blauw deel van de curve in de tekening) die uiteraard snel kleiner wordt vanwege de ontlading van de condensator door de belastingsstroom van R1. Afhankelijk van de mate van afvlakking blijft op de gelijkspanning dus een kleine of grotere wisselspanningscomponent, 'rimpelspanning' genaamd, over. De frequentie van de rimpel is bij deze halve periode gelijkrichting gelijk aan de frequentie van de netspanning (50 Hz) en bij de volle periode gelijkrichting het dubbele daarvan (100 Hz).
Bij de volgende positieve halve periode van de trafospanning gaat de diode alleen geleiden als de trafospanning groter wordt dan de spanning die op dat moment nog over de condensator staat. U ziet dat de diode nu maar heel even gaat geleiden (tweede rood deel van de curve). Gedurende die korte tijd levert de trafo wel een grote stroom die via de diode de condensator weer oplaadt.
 |
| Een condensator als afvlakker van een voedingsspanning. (© 2024 Jos Verstraten) |
Afvlakken van pulsbreedte gemoduleerde spanningen
Pulsbreedte modulatie, in het Engels 'Pulse Width Modulation' (PWM) genoemd, zorgt ervoor dat u de voedingsspanning die u aanbiedt aan een gelijkspanningsbelasting uiterst efficiënt kunt regelen. Bij PWM wordt niet de grootte van de spanning, maar de aan/uit-verhouding (pulsbreedte of duty cycle) geregeld. Als u aan de ingang een gelijkspanning van 12 V aanlegt, zal deze spanning ook aan de uitgang verschijnen. De spanning is echter niet continu aanwezig maar wordt als het ware heel snel in stukjes gehakt, oftewel gepulst. Dit 'in stukjes hakken' gebeurt 300 tot 600 keer per seconde. Meestal gebruikt men hiervoor een MOSFET als schakelaar. Hoe breder deze pulsjes, hoe hoger de gemiddelde waarde van de spanning op de uitgang. Door de breedte van deze spanningspulsjes, de 'duty-cycle', te regelen kunt u dus ook de gemiddelde waarde van de uitgangsspanning regelen. Dat omzetten van de pulsspanning in een gelijkspanning gebeurt door een diode en een elco aan de uitgang van de PWM-regeling te hangen.
 |
| Een condensator als afvlakker van een PWM-regeling. (© 2024 Jos Verstraten) |
4 - De condensator als integrator en differentiator
Inleiding
De reeds besproken RC-combinatie is een van de belangrijkste passieve combinaties die u in de elektronica aantreft. De samenwerking weerstand/condensator kan zich uiten op twee verschillende manieren, namelijk al integrator of als differentiator. Deze schakelingen komen van pas als u een puls in de tijd wilt vertragen of wilt verbreden of versmallen.
Beide zeer fundamentele schakelingen bestaan uit de serieschakeling van een weerstand en een condensator, waarbij het enige verschil is de plaats die beide onderdelen innemen.
De integrator
Deze schakeling is in onderstaande figuur getekend. Het is niets anders dan de reeds bekende RC-kring, waar de spanning over de condensator als uitgang wordt genomen. Als u een smalle spanningspuls op de ingang legt zal deze smalle puls door de condensator breder gemaakt worden. Men spreekt van een integrerende schakeling.
 |
| De werking van de integrator grafisch toegelicht. (© 2024 Jos Verstraten) |
Een integrator rond een op-amp
Een integrator ontleent zijn specifieke eigenschappen aan het toepassen van de condensator in de terugkoppeling van een op-amp. Kijk maar naar onderstaande figuur, waar u het basisschema van een integrator ontdekt. De weerstand staat nu tussen de ingang van de schakeling en de inverterende ingang van de op-amp en de condensator koppelt de uitgangsspanning terug naar de inverterende ingang.
Door het aanleggen van een spanning aan de ingang stuurt u een stroom I door de weerstand R1. Omdat de positieve ingang van de op-amp aan massa ligt, zal ook de inverterende ingang op massa-potentiaal staan. De grootte van de stroom wordt alleen bepaald door de waarde van R1 en door de grootte van de ingangsspanning. De inwendige weerstand van de op-amp is zeer hoog, zodoende kan de stroom I alleen maar via de condensator naar de uitgang van de schakeling vloeien.
Nu is het een gegeven dat een condensator, die wordt doorlopen door een constante stroom, over zichzelf een lineair stijgende (of dalende) spanning opbouwt. Dát nu, is hier het geval. De stroom I is constant zolang u de ingangsspanning niet varieert. De linker plaat van de condensator ligt aan de massa (virtueel nulpunt). De spanning op de rechter plaat en dus aan de uitgang van de schakeling zal lineair stijgen of dalen. De integrator is als het ware een schakeling die onthoudt hoeveel spanning er gedurende een bepaalde tijd aan de ingang wordt aangeboden.
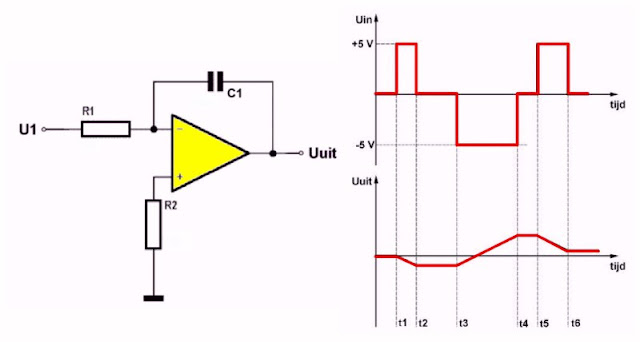 |
| Een integrator met een op-amp. (© 2024 Jos Verstraten) |
De differentiator
Een differentiator is een schakeling, waarvan de grootte van de uitgangsspanning recht evenredig is met de snelheid waarmee de ingangsspanning van waarde verandert. Legt u aan een differentiator een constante spanning, dan zal de uitgangsspanning nul zijn. Verandert de ingangsspanning zeer snel van grootte, dan zal de differentiator een grote uitgangsspanning leveren.
In het onderstaande schema zijn weerstand en condensator van plaats verwisseld. De spanning over de weerstand is nu de uitgangsspanning. Als u een puls aan de schakeling aanbiedt stelt u vast dat er over de weerstand twee veel smallere, naaldvormige pulsen ontstaat. De eerste is positief, de tweede is even groot en breed en negatief. De schakeling kan dus gebruikt worden als pulsversmaller. Uiteraard is de breedte van de naaldpulsen afhankelijk van de waarde van de tijdconstante 𝜏 en dus van de waarde van de toegepaste onderdelen.
Differentiatoren worden vaak toegepast in de elektronica. Een differentiator was dé basisschakeling die ervoor zorgde dat uw oude analoge beeldbuis-TV een stabiel, stilstaand beeld opwekte. Op het moment dat de elektronenstraal weer naar de linkerrand van de beeldbuis moest gaan, werd er in het videosignaal een klein pulsje (lijnsync) opgenomen dat door een differentiator werd gedetecteerd.
Een tweede toepassingsvoorbeeld is een spetteronderdrukker waarmee u het geluid, veroorzaakt door krassen en stofdeeltjes op vinylplaten, kunt onderdrukken. De snelle spanningsvariatie in het geluidssignaal, veroorzaakt door de kras of het stofdeeltje, wordt door een differentiator uit het geluidssignaal gefilterd. De uitgangsspanning van deze schakeling schakelt de versterker dan even naar een lager niveau, zodat de kras niet meer zo storend overkomt.
 |
| De werking van de differentiator grafisch toegelicht. (© 2024 Jos Verstraten) |
5 - De condensator als koppel-element
Een 'muur' tussen twee gelijkspanningen
Reeds is vastgesteld dat een condensator voor gelijkspanning een ideale isolator is. Dat wil zeggen dat, als u aan een condensator een gelijkspanning legt, er eerst een korte stroomstoot door het onderdeel vloeit. De condensator laadt dan op tot de grootte van de aangelegde spanning en nadien zal er niets meer gebeuren. Van deze eigenschap kunt u dankbaar gebruik maken als u twee punten, die op een verschillende gelijkspanning staan, met elkaar moet verbinden. De condensator dient dan als koppel-element, die wél eventuele wisselspanning van de ene schakeling naar de andere door koppelt, maar de niet gelijke gelijkspanningen netjes in de eigen schakelingen laat. Men spreekt bij deze specifieke toepassing dan ook van 'koppelcondensator'.
Voorbeeld 1: twee transistortrappen scheiden
Het schema is getekend in de onderstaande figuur. De collector van T1 is, zoals dat meestal het geval is, ingesteld op ongeveer de helft van de voedingsspanning. De basis van T2, daarentegen, is ingesteld op een spanning die 0,65 V hoger is dan de spanning op de emitter. Deze laatste is niet zo groot, zodat ook de basis op ten hoogste 2 á 3 V staat. Nu is het wel de bedoeling dat het wisselspanningssignaal op de collector van T1 doorgekoppeld wordt naar de basis van T2. Tussen beide trappen moet dus een onderdeel worden geplaatst dat wél de wisselspanning, maar niet de gelijkspanning doorlaat. En dat is uiteraard de condensator C1. De waarde van die condensator is afhankelijk van de laagste frequentie die u wilt versterken. Hoe lager die frequentie, hoe groter de condensator moet zijn. Als u een elco toepast moet u er op letten dat de spanning Uc1 per definitie groter is dan de spanning Ub2 en dat de positieve aansluiting van de elco dus aan de collector van T1 moet komen.
 |
| Het gebruik van een koppelcondensator tussen twee versterkertrappen. (© 2024 Jos Verstraten) |
Voorbeeld 2: onderdrukken van schakelklikken
Bij het toepassen van koppelcondensatoren in audio-schakelingen kan er toch nog een probleem ontstaan. Als u klikken hoort op het moment dat u een schakelaar omschakelt, betekent dit dat niet alle contacten van de schakelaar op dezelfde spanning staan. Er kunnen dan bij het schakelen korte oplaadstroompjes vloeien, die de klikken of zelfs ploppen uit de luidsprekers veroorzaken.
De oorzaak van het probleem is geschetst in het linker schema van onderstaande figuur. Een omschakelaar S1 is opgenomen tussen de uitgang van een trap en de ingang van de volgende. Beide signalen worden via condensatoren uit- en ingekoppeld. In de getekende stand van de schakelaar in contact 'c' nergens mee verbonden, hangt dus vrij in de lucht. Door de lekweerstand van de condensator C1 zal de spanning op contact 'c' gelijk worden aan de spanning UA. Hetzelfde geldt voor het moedercontact, dat opgeladen zal worden tot de spanning UB.
Als u nu de schakelaar in stand 'c' zet zal er opeens een rechtstreekse verbinding tussen de twee condensatoren tot stand komen. Als UA niet gelijk is aan UB (en dat zal meestal het geval zijn) zal er een korte, maar flinke stroom door de twee condensatoren gaan vloeien, totdat de spanningen op het moedercontact en contact 'c' van de schakelaar S1 aan elkaar gelijk zijn. Het is deze stroom die de schakelklik veroorzaakt.
In het rechter schema is de eenvoudige oplossing voor dergelijke problemen geschetst. Alle contacten van de schakelaar worden via grote weerstanden (100 kΩ tot 1 MΩ) met de massa verbonden. Deze waarden zijn zeer laag vergeleken met de lekweerstanden van de condensatoren. Het gevolg is dat er geen gelijkspanningen over de weerstanden worden opgebouwd en dat alle schakelaarcontacten op 0 V staan. Bij het schakelen kunnen er dus geen stromen vloeien en de schakelklikken of -ploppen blijven afwezig.
 |
Het vermijden van schakelklikken. (© 2024 Jos Verstraten) |
6 - De condensator, aangesloten op wisselspanning
Oneindig wordt eindig
In een vorige paragraaf van dit artikel is vastgesteld dat als u een condensator aansluit op een gelijkspanning, het onderdeel zich even zal opladen tot deze spanning. Nadien houdt iedere actie op tot u de condensator ontlaadt door hem over een weerstand kort te sluiten.
Als u echter de condensator voortdurend laat op- en ontladen, bijvoorbeeld door de omschakelaar van in een van de vorige figuren voortdurend om te switchen, dan zal er een continue maar in grootte wisselende stroom door de condensator gaan lopen. Immers, als de schakelaar in de bovenste stand staat wordt de batterijspanning Ub aangeboden aan de serie-schakeling van weerstand en condensator en zal deze laatste zich gaan opladen tot de batterijspanning. Als u even later de schakelaar ompoolt wordt de serieschakeling van R en C met massa verbonden en zal de condensator zich gaan ontladen.
Hieruit kunt u dus reeds een zeer belangrijke conclusie trekken. Als u er voor zorgt dat de spanning die aan een condensator wordt aangeboden niet constant blijft (dus iets anders is dan een zuivere gelijkspanning) zal de condensator reageren door het volgen van die spanningsvariaties. Nu weet u uit de wet van Ohm dat er in een keten een weerstand aanwezig is, als het aanleggen van een spanning aan die keten het vloeien van stroom door die keten tot gevolg heeft. Met andere woorden, een condensator die aangesloten is op een variërende spanning, zal géén isolator meer zijn maar een soort van weerstand. Als de spanning die aan de keten wordt aangeboden varieert, zal er stroom door het systeem vloeien. Alvorens dieper in te gaan op het wezen van die weerstand, wordt de condensator aangesloten op een echte wisselspanning, bijvoorbeeld een sinusvormige spanning.
De condensator, aangesloten op een sinusvormige wisselspanning
In de onderstaande figuur wordt nog eens duidelijk aangetoond hoe een condensator zich verschillend gedraagt als hij wordt aangesloten op een constante of op een variërende spanning.
Als u die condensator C via de serieweerstand R aansluit op een sinusvormige wisselspanning (rechts getekend) wil de condensator altijd opladen tot de momentane waarde van die wisselspanning. Maar omdat de waarde van de wisselspanning steeds verandert zal de spanning over de condensator altijd iets achter lopen op die wisselspanning. Door de serieweerstand vloeit dus altijd een wisselstroom die probeert de spanning over de condensator gelijk te maken aan de variërende spanning aan de ingang, maar daar nooit in slaagt. Er vloeit nu dus steeds een stroom door de RC-kring, waaruit u kunt besluiten dat een condensator voor wisselspanning altijd een bepaalde weerstand heeft. Het gevolg van het vloeien van deze stroom is dat er een wisselspanning valt over de weerstand R, waardoor de spanning over de condensator C altijd kleiner zal zijn dan de spanning aan de ingang van de RC-kring.
 |
Van oneindige naar eindige weerstand. (© 2024 Jos Verstraten) |
De impedantie Z van een condensator
Zoals bekend uit de wet van Ohm bestaat er een bepaald verband tussen de weerstand van een keten, de spanning die over die keten staat en de stroom die door de onderdelen van het systeem loopt. Dat verband wordt in formule-vorm uitgedrukt door:
U = I • R
De spanning over een systeem is gelijk aan de weerstand in het systeem, vermenigvuldigd met de stroom die door het systeem vloeit.
In de vorige paragraaf is aangetoond dat, als u aan een condensator een wisselspanning aanlegt, er door die condensator een wisselstroom vloeit. Volgens de wet van ohm moet die condensator dus een weerstand bezitten. Omdat dit verschijnsel alleen maar optreedt als de condensator met wisselspanning wordt gevoed wordt, noemt men die weerstand de 'impedantie' van de condensator. De eenheid van impedantie is, net zoals die van weerstand, de ohm en de impedantie wordt in de wiskunde voorgesteld door de letter 'Z'.
De impedantie Z is niet constant!
De waarde van een condensator wordt uitgedrukt in farad. Op een of andere manier moet er dus een verband bestaan tussen de waarde van de condensator in farad en de impedantie in ohm. Het blijkt dat de wisselstroomweerstand van een condensator ook wordt bepaald door de waarde van de frequentie van de wisselspanning die over de condensator staat. Dat is, na enig nadenken, ook vrij logisch. Immers, hoe hoger de frequentie, hoe sneller de spanning die aan de condensator wordt aangeboden verandert en hoe meer stroom er door de keten moet vloeien om die spanningsvariaties bij te benen. Een ding is dus duidelijk: als de frequentie van het signaal groter wordt, dan gaat ook de stroom stijgen, wat dus neer komt op een verlaging van de impedantie van de condensator.
Anderzijds is het ook duidelijk dat de stroom in de keten groter wordt als de waarde van de condensator stijgt. Hoe groter de condensator, hoe meer elektronen uit de spanningsbron naar de platen van de condensator getransporteerd moeten worden om de condensatorspanning gelijke tred te laten houden met de wisselspanning aan de ingang van de keten. De impedantie van een condensator neemt dus af als de waarde van de condensator stijgt.
Die twee intuïtief aan te voelen waarheden kunnen vertaald worden naar de volgen de vrij eenvoudige wiskundige uitdrukking:
Zc = 1 / [2 • π • f • C]
waarin:
- Zc de impedantie van de condensator is, uitgedrukt in Ω
- π het getal 'pi' is, gelijk aan 3,1415
- f de frequentie van de wisselspanning is, uitgedrukt in Hz
- C de capaciteit van de condensator is, uitgedrukt in F
De waarde van de impedantie bij 1 kHz
Die formule zegt uiteraard niet erg veel. Om u een indruk te geven hoe de impedantie van een condensator varieert in functie van de capaciteitswaarde hebben wij de impedantie van diverse condensatoren met de gegeven formule berekend bij een frequentie van 1 kHz.
 |
| De impedantie van condensatoren bij 1 kHz. (© 2024 Jos Verstraten) |
Laat goed tot u doordringen wat dit betekent! Als u een sinusgenerator die een signaal levert met een frequentie van 1 kHz aansluit op een condensator van 100 μF komt dit op hetzelfde neer alsof u die generator belast met een weerstand van 1,59 Ω! Een vrijwel perfecte kortsluiting en veel signaal kunt u dus niet uit die generator verwachten.
7 - De condensator als terugkoppel element
Inleiding
Nadat in de vorig paragrafen enige recht-toe-recht-aan toepassingen van de condensator zijn besproken, komen nu meer verfijnde toepassingen van de condensator aan de orde. Toepassingen, waarbij de condensator niet rechtstreeks in de signaalloop is opgenomen, maar waar de condensator gebruikt wordt in een terugkoppeling. Een van de voornaamste toepassingen hiervan is het beïnvloeden van de weergavekarakteristiek van een schakeling.
Terugkoppeling (feedback)
Het fundamentele verschil tussen rechtstreekse toepassingen van een condensator en die waarbij het onderdeel als terugkoppel-element gebruikt wordt, volgt uit de onderstaande figuur. In het bovenste schema staan enige condensatoren, gebruikt als rechtstreeks element. De onderdelen zitten namelijk rechtstreeks in de signaalloop. Zo moet het signaal, dat aan de ingang van de schakeling wordt gelegd, eerst door condensator C1 gaan alvorens het aan de ingang van de eerste trap komt. Hetzelfde geldt voor condensator C2. Ook condensator C3 werkt rechtstreeks op het signaal in. Weliswaar moet het signaal niet doorheen dit onderdeel, wil het zijn weg door de schakeling vervolgen, maar de condensator zal wel rechtstreeks zijn invloed op het signaal doen gelden.
Bij tegenkoppeling, zoals getekend in het onderste schema, gaat het er heel anders aan toe. De twee getekende condensatoren C1 en C2 zitten niet in de weg van het signaal. Toch zullen de condensatoren wel degelijk invloed op de werking van de schakeling hebben. Via de condensatoren wordt immers een bepaald gedeelte van het uitgangssignaal van een bepaalde trap teruggekoppeld naar de ingang van een bepaalde trap.
 |
| Het principe van terugkoppeling. (© 2024 Jos Verstraten) |
Meekoppeling en tegenkoppeling
Er bestaan twee soorten terugkoppeling: meekoppeling en tegenkoppeling. In het eerste geval zal de terugkoppeling een versterkend effect op de werking van de schakeling hebben. Het teruggekoppelde signaal versterkt dan als het ware het aanwezige ingangssignaal. Bij tegenkoppeling zal het teruggekoppelde signaal een tegenwerkende of verzwakkende invloed op het aanwezige ingangssignaal uitoefenen.

Capacitieve tegenkoppeling bij een op-amp versterker
Als u een versterkertrap ontwikkelt, kan het uw bedoeling zijn dat slechts een bepaalde frequentieband wordt versterkt. Denk bijvoorbeeld aan een microfoonversterker, waar wel de frequenties uit het spraakspectrum moeten worden versterkt, maar niet de steeds aanwezige hoogfrequente ruis. Ook kan het voorkomen dat u de hoge frequenties, die tóch van geen nut zijn, niet wilt versterken omdat die onnodige versterking toch alleen maar narigheid, zoals oscillaties, tot gevolg zal hebben.
Een terugkoppeling door middel van een condensator is een uitstekend middel om dit doel te bereiken. U weet inmiddels dat een condensator een impedantie heeft die afhankelijk is van de frequentie van het signaal. Hoe hoger de frequentie, hoe lager de impedantie.
Een eenvoudig voorbeeldje van een dergelijke vorm van terugkoppeling is getekend in de onderstaande figuur. Het te versterken ingangssignaal wordt aangeboden aan de positieve ingang van de op-amp. De mate van versterking wordt ingesteld door middel van twee weerstanden, R1 en R2.
Als de te versterken spanning gelijk is aan bijvoorbeeld 1 V en de spanningsdeler is zo gekozen dat een tiende van de uitgangsspanning op de negatieve ingang belandt, dan zal de versterking van de trap gelijk zijn aan tien. De op-amp zal zichzelf immers zo instellen, dat de spanning op de negatieve ingang gelijk wordt aan de 1 V op de positieve ingang. Dat kan alleen als de uitgangsspanning van de schakeling gelijk wordt aan 10 V.
De condensator zal er echter voor zorgen dat de spanningsdeler tussen uitgang en negatieve ingang frequentie-afhankelijk wordt. Voor lage frequenties is de impedantie van de condensator zeer groot en is zijn aanwezigheid te verwaarlozen. Als de frequentie van het signaal stijgt zal de impedantie van de condensator gaan dalen. De totale weerstand tussen uitgang en negatieve ingang wordt dan gelijk aan de parallelschakeling van de vaste weerstand R1 en de variabele weerstand van de condensator. Hoe hoger de frequentie, hoe lager deze totale weerstand zal worden. Met andere woorden: als de frequentie stijgt zal een groter deel van de uitgangsspanning teruggekoppeld worden naar de negatieve ingang van de op-amp. De uitgangsspanning moet dan niet meer gelijk zijn aan 10V, om de spanning op de negatieve ingang gelijk te maken aan de 1 V op de positieve ingang. De versterking van de schakeling gaat dalen. Het zal duidelijk zijn dat de versterkingsdaling toeneemt als de frequentie stijgt.
Dat is weergegeven door de zogenaamde 'frequentie/amplitude-karakteristiek' rechts in de onderstaande figuur. U ziet hier de versterking van de trap in dB, getekend in functie van de frequentie.
 |
| Capacitieve tegenkoppeling bij een op-amp versterker. (© 2024 Jos Verstraten) |
Capacitieve tegenkoppeling bij een transistor versterker
Hetzelfde grapje kunt u natuurlijk ook uithalen bij een versterkertrap die is opgebouwd rond een transistor, zie de onderstaande figuur. De transistor wordt ingesteld door middel van de twee basisweerstanden en hun soortgenoten in collector en emitter. De versterking is gelijk aan de verhouding van R3 tot R4. De tegenkoppeling wordt nu gevormd door de condensator C2, geschakeld tussen basis en collector. Voor lage frequenties speelt dit onderdeel niet mee. Voor hoge frequenties wordt de impedantie van C1 zo laag dat een gedeelte van de spanning op de collector op de basis belandt. Nu zijn de spanningen op basis en collector in tegenfase. Als de spanning op de basis stijgt, dan zal de spanning op de collector dalen. Omdat de spanning op de collector in tegenfase is met de spanning op de basis, zal de terugkoppeling ervoor zorgen dat het signaal op de basis kleiner wordt. Het gevolg is dat de hoge frequenties minder versterkt worden dan de lage frequenties.
 |
| Capacitieve tegenkoppeling bij een transistor versterker. (© 2024 Jos Verstraten) |
Het beïnvloeden van de weergave van lage frequenties
Hoewel dit niet zo vaak in de praktijk gevraagd wordt, is het tóch denkbaar dat voor sommige toepassingen de versterking van een trap voor lage frequenties lager moet zijn dan voor hoge frequenties. Ook hier kunt u door het invoeren van een condensator in een tegenkoppeling bereiken wat gevraagd wordt. Een voorbeeldje van zo'n schakeling is getekend in de onderstaande figuur.
Voor hoge frequenties heeft de condensator een zeer kleine impedantie, zodat deze te verwaarlozen is ten opzichte van de waarde van de weerstand R2. De versterking wordt dan bepaald door de verhouding van de beide weerstanden R1 en R2. Als de frequentie van het ingangssignaal daalt zal de impedantie van de condensator steeds groter worden, zodat hij niet meer te verwaarlozen is ten opzichte van de waarde van de weerstand R2. Het gevolg is dat er tussen de negatieve ingang en de massa een groter wordende weerstand komt te staan, zodat er een groter gedeelte van de uitgangsspanning op de negatieve ingang wordt aangeboden. De schakeling dus minder gaan versterken.
 |
| Beïnvloeden van de weergave van lage frequenties. (© 2024 Jos Verstraten) |

