
|
Met deze spotgoedkope speciale trafo kunt u de netspanning galvanisch geïsoleerd omzetten in een kleine recht evenredige gelijkspanning die u in een schakeling veilig kunt verwerken, loggen en meten. |
Nauwkeurige meten van de netspanning
Galvanisch scheiden, reduceren en omzetten in een gelijkspanning
Soms moet u de waarde van de netspanning nauwkeurig meten. Voorbeelden zijn het meten van een door een verbruiker opgenomen vermogen of het loggen van het verloop van de netspanning over één dag.
Bij het meten van de netspanning doet zich een aantal problemen voor:
- Galvanische scheiding:
Het is absoluut verboden een elektronische schakeling rechtstreeks te verbinden met de netspanning (een triac-dimmer is de uitzondering op deze regel). Tussen de fase en de aarde staat immers een spanning die, onder bepaalde omstandigheden, dodelijk kan zijn. Tussen de twee aders waarop de netspanning staat en uw meetschakeling moet u een in theorie oneindig hoge weerstand meten. Alleen dan kunt u veilig gelijk welk punt van uw schakeling aanraken. Zo'n systeem noemt men een 'galvanische scheiding' tussen het net en uw schakeling. - Reduceren:
De netspanning is uiteraard veel te groot om aan uw meetschakeling aan te bieden. U moet dus een systeem verzinnen om de netspanning te reduceren tot een waarde die bijvoorbeeld kleiner is dan 5 V, zodat zij door de ADC in een microcontroller kan worden verwerkt. - Omzetten in een gelijkspanning:
Als u de waarde van de netspanning nauwkeurig wilt meten of loggen moet u deze omzetten in een gelijkspanning. De meeste ADC's werken immers unipolair. - Constante schaalfactor:
Tussen de wisselspanning aan de ingang en de gelijkspanning aan de uitgang moet een bepaalde schaalfactor α bestaan die constant is:
Uuit = α • Uin
Alleen dán wordt de wisselspanning nauwkeurig gemeten, of zij nu 207 V of 253 V groot is.
Waarom kunt u geen gewone voedingstrafo gebruiken?
Deze problemen zou u, zo lijkt het, eenvoudig kunnen oplossen door een gewone voedingstrafo van 230 V naar 6 V op het net aan de sluiten en de secundaire spanning gelijk te richten, zie de onderstaande figuur. U kunt dan de schaalfactor α bepalen tussen de netspanning en de uitgangsspanning van de gelijkrichter. Als u bijvoorbeeld exact 230 V aan de trafo aanlegt en op de uitgang van de schakeling staat een gelijkspanning van 8,49 V, dan is de schaalfactor α gelijk aan 8,49 V gedeeld door 230 V is 0,037 of 37 • 10-3.
Als de netspanning zou stijgen tot 245 V, dan verwacht u uiteraard dat de uitgangsspanning van de schakeling gelijk wordt aan 9,065 V. Helaas is dat niet het geval en dat wordt veroorzaakt door het feit dat een gewone nettrafo geen lineair werkende omzetter is.
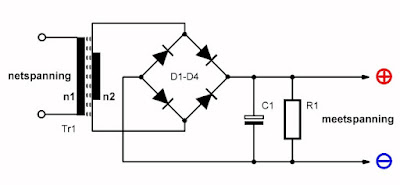 |
| Een eenvoudig schema dat echter niet nauwkeurig genoeg werkt. (© 2024 Jos Verstraten) |
De BH-curve gooit roet in het eten
Volgens de transformator theorie is de verhouding tussen de primaire spanning en de secundaire spanning van een trafo gelijk aan de wikkelverhouding tussen n1 en n2. Dat geldt echter alleen voor een ideale theoretische trafo zonder gebreken. De kern van de trafo is echter alles behalve ideaal en heeft veel last van een verschijnsel dat 'magnetische verzadiging' heet.
Hoe werkt een nettrafo? Als u aan de primaire wikkeling een wisselspanning legt gaat er door die wikkeling een wisselstroom vloeien. Die stroom wekt rond deze spoel een magnetisch veld op waarvan de grootte wordt gegeven door de magnetische veldsterkte H, uitgedrukt in A/m. Die veldsterkte wekt in de ijzeren kern van de trafo een bepaalde magnetische flux Φ op, waarvan de grootte wordt bepaald door de magnetische fluxdichtheid B. Deze flux, uitgedrukt in Tesla, is verantwoordelijk voor het ontstaan van de secundaire spanning. Het probleem is dat tussen de grootheden H en B geen lineair verband bestaat. Als H verdubbelt zou ook B moeten verdubbelen. Dit is echter niet het geval, de waarde van B stijgt minder snel dan de waarde van H. Dit verschijnsel wordt grafisch voorgesteld in de beroemde 'BH-curve' van een trafo. Het wordt veroorzaakt door het feit dat, naarmate de waarde van B stijgt, er steeds minder atomen in de kern van de trafo aanwezig zijn die nog niet 'gemagnetiseerd' zijn.
Met zegt dat de kern langzaam maar zeker 'verzadigd' raakt.
 |
| De BH-curve van de kern van een voedingstrafo. (© 2024 Jos Verstraten) |
De gevolgen voor een nettrafo
De magnetische verzadiging van de kern van een trafo komt duidelijk tot uiting als u de secundaire spanning observeert op uw oscilloscoop. U ziet een duidelijke afplatting van de toppen van de sinussen. Als de waarde van H stijgt zal de waarde van B immers niet proportioneel mee stijgen. Het gevolg is dat dezelfde vervorming aanwezig is op de spanning die door B in de secundaire wikkeling wordt gegenereerd. Voor een voedingstrafo is dit verschijnsel van geen belang. Als u echter een trafo moet gebruiken om de primaire spanning heel nauwkeurig met een constante schaalfactor α om te zetten in een galvanisch gescheiden en meetbare spanning is een normale nettrafo een zeer slechte keuze. De waarde van de schaalfactor α varieert veel te veel!
 |
| Vervorming van de secundaire trafo-spanning. (© 2024 Jos Verstraten) |
De stroomtransformator ZMPT101B
Kennismaking
De ZMPT101B ziet er uit zoals iedere gewone laagvermogen voedingstrafo, hij heeft een primaire wikkeling en een secundaire wikkeling. Maar daar houden de gelijkenissen mee op! Bij een nettrafo is het de bedoeling dat een primaire spanning wordt omgezet in een secundaire spanning. Bij de ZMPT101B is het de bedoeling dat een heel kleine primaire stroom wordt omgezet in een even kleine secundaire stroom. En als wij schrijven 'kleine stroom' dan bedoelen wij 'kleine stroom'. Deze stroomtrafo wordt gespecificeerd met een werkstroom van slechts 2 mA!
Het voordeel is dat er dan absoluut geen sprake is van verzadiging van de kern en dat er dus in het zeer kleine lineaire deel van de BH-curve wordt gewerkt.
 |
| De stroomtransformator ZMPT101B. (© AliExpress) |
Fabrikant, prijs en specificaties
De ZMPT101B wordt gefabriceerd door de Chinese NanJing ZeMing Electronic Co. Het onderdeel wordt via de bekende Chinese internetkanalen zoals AliExpress aangeboden voor een stukprijs van minder dan één euro. De trafo zit in een lichtblauwe kunststof behuizing van 19,2 mm bij 16,7 mm bij 18,6 mm. Deze behuizing is volgegoten met epoxyhars. De pennen van de twee wikkelingen staan 12,7 mm uit elkaar, de afstand tussen de primaire en secundaire pennen bedraagt 10 mm.
 |
| De afmetingen van de ZMPT101B. (© NanJing ZeMing) |
Volgens de fabrikant voldoet de ZMPT101B aan de onderstaande specificaties:
- Maximale stromen: 10 mA
- Advies primaire stroom: 2 mA
- Advies secundaire stroom: 2 mA
- Wikkelverhouding: 1.000/1.000
- Interne weerstand: 120 Ω
- Fasehoek tussen prim. en sec.: 20' max. bij 2 mA en 100 Ω afsluitweerstand
- Lineariteit: beter dan ±0,2 % bij 2 mA en 100 Ω afsluitweerstand
- Isolatiespanning tussen prim. en sec.: 4.000 V
- Advies afsluitweerstand: 100 Ω
- Frequentiebereik: 50 Hz ~ 60 Hz
- Afmetingen: 19,2 mm x 16,7 mm x 18,6 mm
- Gewicht: 13,1 g
De transferkarakteristiek van de ZMPT101B
De transferkarakteristiek geeft het verband tussen de primaire stroom Iin en de secundaire spanning Uuit die wordt gegenereerd over een bepaalde afsluitweerstand. Dit verband is weergegeven in de onderstaande grafiek voor drie verschillende afsluitweerstanden.
 |
| De transferkarakteristiek van de ZMPT101B. (© 2024 Jos Verstraten) |
Het standaardschema rond de ZMPT101B
In de onderstaande figuur is het meest eenvoudige schema rond deze stroomtrafo getekend. De primaire wikkeling wordt via een serieweerstand R1 aangesloten op de te meten wisselspanning. Deze weerstand moet u uiteraard zo berekenen dat de stroom Iin door de primaire ongeveer gelijk is aan de geadviseerde 2 mA. De uitgangsstroom van de trafo wordt in een meetbare spanning omgezet door de belastingsweerstand R2.
De uitgangsspanning wordt gegeven door de formule:
Uuit = [Uin / R1] ● R2
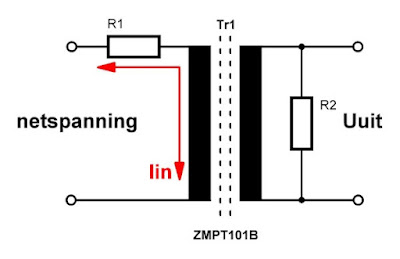 |
| Het standaardschema rond de ZMPT101B. (© 2024 Jos Verstraten) |
Het standaard printje met de ZMPT101B
Een kant-en-klare oplossing voor € 3,45
U kunt uiteraard zélf een schakeling en printje ontwerpen rond deze stroomtrafo. Maar waarom zou u dit doen als u een kant-en-klaar printje kunt aanschaffen?
Het in de onderstaande foto voorgestelde printje in uiteraard van Chinese herkomst en wordt via alle bekende internet-kanalen aangeboden voor de ongelofelijke prijs van iets meer dan één euro. Mét verzending betaalt u er bij AliExpress € 3,45 voor.
 |
| Het standaard printje met de ZMPT101B. (© AliExpress) |
Eigenschappen
Het printje meet slechts 51 mm bij 21 mm en is aan een kant voorzien van een printkroonsteentje waarop u de te meten netspanning aansluit. Aan de andere kant staat een Molex printheader met vier contacten:
- 2 x massa.
- +5 Vdc voeding.
- Uuit.
In de onderstaande foto zijn beide zijden van het printje verenigd.
 |
| Beide zijden van het printje. (© 2024 Jos Verstraten) |
Het schema van het printje
Het is niet zo ingewikkeld om uit de bovenstaande foto het schema van de schakeling af te leiden. Dat hebben wij gedaan met het onderstaand resultaat.
Het schema bestaat in feite uit niets meer dan twee achter elkaar geschakelde identieke inverterende versterkers met een versterkingsfactor van tien. Tussen beide versterkers is de instelpotentiometer R12 opgenomen waarmee u de waarde van de schaalfactor α kunt instellen. Zoals u ziet zijn de positieve ingangen van beide op-amp's ingesteld op de helft van de voedingsspanning via de weerstandsdelers R2/R3 en R10/R11. Dat betekent dat ook de uitgangen van de op-amp's in rust op de helft van de voedingsspanning staan. De versterkte secundaire spanning van de trafo wordt dus gesuperponeerd op deze instelspanning. Op de uitgang staat een 50 Hz wisselspanning die op en neer gaat rond +2,5 V. Er is geen gelijkrichter aanwezig, daar moet u zélf voor zorgen.
Vreemd is de keuze van R13 als 820 kΩ. Bij een ingangsspanning van 230 V vloeit er een stroom van slechts 0,28 mA door de primaire van de trafo. Dat is dus heel wat minder dan de geadviseerde 2 mA!
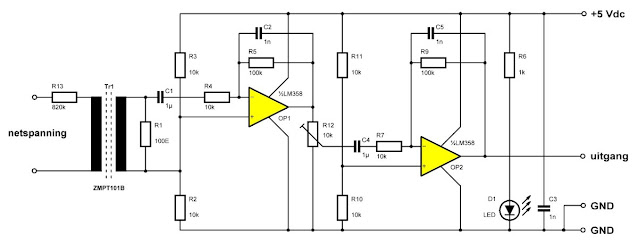 |
| Het schema van het printje. (© 2024 Jos Verstraten) |
Verwerken van de uitgangsspanning met een Arduino
Als u een beetje kunt programmeren hoeft u het printje niet eens af te sluiten met een nauwkeurige gelijkrichter. Op internet zijn voldoende programma's te vinden waarmee u de uitgang van dit printje rechtstreeks kunt verwerken met een Arduino. De code bepaalt dan de topwaarde op de uitgang van het printje, trekt daar de instelspanning van af, houdt rekening met de schaalfactor α en zet de aldus berekende amplitude om naar de effectieve waarde.
 |
| De netspanning loggen met een Arduino. (© electropeak) |
ATTENTIE!
Het is merkwaardig dat Chinese ontwerpers soms een in wezen uitstekend ontwerp kunnen verzieken door er een stomme fout in te bouwen. Ook bij dit printje is dat het geval. Over de weerstand R13 valt vrijwel de volledige netspanning. Tóch hebben de ontwerpers er voor gekozen deze weerstand uit te voeren onder de vorm van een SMD-weerstand van het type 2012 (metrische standaard) of type 0805 (imperiale standaard). Zo'n onderdeeltje is maar 2,0 mm groot en tussen de twee pad's waarop deze weerstand wordt gesoldeerd staat dus een spanning die kan oplopen tot 250 Veffectief! Volgens de specificaties mag er over zo'n weerstand echter een maximale spanning staan van slechts 150 V. Dat is dus een zware en onvergeeflijke ontwerpfout, die gelukkig gemakkelijk is te corrigeren. Verwijder het weerstandje R13, zet een soldeerklodder over beide pad's en sluit de netspanning aan op het kroonsteentje via twee ½ W axiale weerstandjes van 412 kΩ, eentje in serie met de fase en eentje in serie met de nul. Probleem opgelost!
Een testje van een van deze printjes
Instellen van de potentiometer R12
Met deze potmeter kunt u, zoals reeds geschreven, de schaalfactor van de schakeling instellen. In de onderste stand verschijnt er helemaal geen wisselspanning op de uitgang. In de bovenste stand wordt de tweede op-amp overstuurd, zodat de uitgangsspanning wordt geclipt. Bij ons printje kon de uitgangsspanning worden opgevoerd tot 0,77 Veffectief (bij exact 230 V ingangsspanning) alvorens er sprake was van clipping.
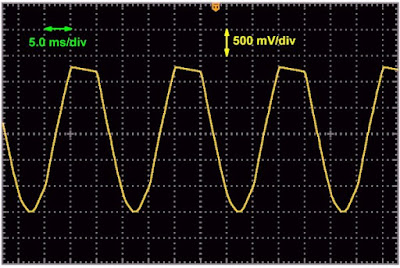 |
| Clipping van de uitgangsspanning van het printje. (© 2024 Jos Verstraten) |
De uitgangsspanning van het printje
Om er zeker van te zijn dat wij ver uit de buurt van clipping blijven hebben wij de instelpotentiometer zo afgeregeld tot er een spanning van 400 mVeffectief uit het printje komt bij een ingangsspanning van 230 V. In het onderstaande oscillogram ziet u hoe die spanning er uitziet. De blauwe lijn geeft het GND-niveau weer. De wisselspanning is dus inderdaad mooi gesuperponeerd op een instelspanning van +2,5 Vdc!
 |
De uitgangsspanning van het printje. (© 2024 Jos Verstraten) |
Meten van de lineariteit
Om de lineariteit van de omzetting te beoordelen hebben wij het printje aangesloten op een variac en negen verschillende effectieve wisselspanningen tussen 10 V en 250 V aangeboden. De exacte waarde van de in- en uitgangsspanningen worden gemeten met onze ET3255 multimeter van East Tester. De verhouding tussen de uit- en de ingangsspanning geeft uiteraard de waarde van de schaalfactor α.

In de onderstaande tabel hebben wij onze metingen samengevat. Hieruit blijkt duidelijk dat de schakeling lineair werkt bij ingangsspanningen tussen 40 V en 250 V. Voor lagere spanningen is er duidelijk een afwijking in het lineaire gedrag, maar voor dergelijke lage wisselspanningen is de stroomtrafo niet ontworpen.
Voor de niet wiskundig onderlegde lezer(es). Om de resultaten overzichtelijk weer te geven hebben wij de schaalfactor voorgesteld als een macht van tien. De notatie '● 10-3' wil zeggen dat u het voorgaande getal moet vermenigvuldigen (●) met 0,001. De schaalfactor bij een ingangsspanning van 50,03 V is dus:
1,734 ● 0,001 = 0,001734
 |
| Controleren van de lineariteit van het printje. (© 2024 Jos Verstraten) |

