
|
De decibel (dB) is bedacht voor het meten van geluidsniveaus, maar wordt ook veel gebruikt in de analoge elektronica voor het definiëren van de verhouding tussen twee identieke grootheden. 
|
Over decibel, versterking en logaritmen
Het begrip bel
De decibel is, net zoals de decimeter het tiende deel van een meter is, het tiende deel van een bel. De bel is echter geen grootheid zoals de volt of de ampère dat zijn. De bel is een getal dat iets zegt over de logaritmische verhouding tussen twee spanningen, twee drukken of twee vermogens. In de elektronica gaat het meestal over de verhouding van twee spanningen en daar gaan wij onze uitleg dan ook op baseren.
Het beschrijven van de versterking van een schakeling
Stel dat u een analoge voorversterker hebt ontworpen en u wilt graag weten hoeveel deze schakeling versterkt. Dan legt u een kleine wisselspanning aan de ingang, bijvoorbeeld 10 mV, en meet de uitgangsspanning. Als die uitgangsspanning 316,2 mV is, dan kunt u besluiten dat die mooie voorversterker 316,2 mV gedeeld door 10 mV, is 31,62 maal versterkt. Dat is dus zeer eenvoudig en in feite bestaat er helemaal geen behoefte om hiervoor een nieuw begrip, de decibel, in te voeren.
Trappen achter elkaar
Zo'n versterkertrap staat echter, zoals getekend in onderstaande figuur, meestal niet alleen. Hij is een onderdeel van een versterkersysteem met voorversterker, toonregeling, balansregeling, volumecontrole en eindversterker. Iedere trap heeft een bepaalde versterking of verzwakking. Een verzwakking wordt uiteraard weergegeven door een versterking die kleiner is dan een. Als u nu de totale versterking of verzwakking wilt weten, dan moet u de deelversterkingen, die in iedere trap zijn ingetekend, met elkaar gaan vermenigvuldigen. In het getekende voorbeeld moet u ongetwijfeld een rekenmachine inschakelen om de totale versterking van het apparaat te berekenen. Inderdaad, de vermenigvuldiging
31,62 ● 0,631 ● 1,41 ● 0,70
maakt u niet uit uw hoofd. Met de rekenmachine komt u uit op een totale versterking van 19,69. Dat is natuurlijk niet zo handig. Vandaar dat men gezocht heeft naar een methode waarbij u de totale versterking van het systeem kunt bepalen door de verschillende versterkingen van de afzonderlijke trappen eenvoudig bij elkaar op te tellen.
 |
| Een complete versterker bestaat uit een aantal trappen met ieder een eigen versterking of verzwakking. (© 2018 Jos Verstraten) |
Die methode heeft men gevonden door het invoeren van een nieuw begrip, de decibel. In wiskundige termen uitgedrukt is de decibel 20 keer het logaritme met grondtal 10 van de verhouding van de uitgangsspanning tot de ingangsspanning van een schakeling. Of in formulevorm:
Adb = 20 ● log [Uuit / Uin]
Logaritme met grondtal 10
Nu zegt het begrip 'logaritme met grondtal 10' u waarschijnlijk helemaal niets. Dat is ook niet erg, want in de dagelijkse elektronica-praktijk hebt u daar niets mee te maken. De logaritme is een moeilijk begrip uit de wiskunde. Om dit begrip duidelijk te maken aan wiskundige leken zouden wij kunnen beweren dat ieder natuurlijk getal een soort 'broertje' heeft, dat de logaritme van dat natuurlijk getal wordt genoemd. Als u het natuurlijk getal steeds groter laat worden zult u merken dat het logaritmisch 'broertje' wél stijgt, maar veel minder snel dan het natuurlijk getal. In onderstaande grafiek is dit verduidelijkt. Op de horizontale as hebben wij de natuurlijke getallen van 0 tot en met 1.000 uitgezet. Op de verticale as staan hun logaritmische 'broertjes'. U ziet dat de logaritme met grondtal 10 van het natuurlijk getal 10 gelijk is aan 1. Het natuurlijk getal 100 heeft een logaritmisch 'broertje' van slechts 2. Het getal 1.000 gaat vergezeld van een logaritmisch equivalent van slechts 3. Met de logaritmen kunt u dus grote natuurlijke getallen door veel kleinere getallen voorstellen, hetgeen het rekenen ermee vergemakkelijkt.
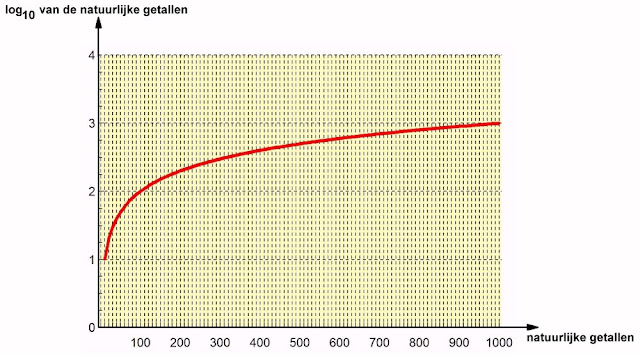 |
| Het verband tussen de natuurlijke getallen en hun logaritmen met grondtal 10. (© 2018 Jos Verstraten) |
Wij schreven al dat u in de dagelijkse elektronica-praktijk niets met die moeilijke logaritmen te maken krijgt. Er zijn namelijk handige tabelletjes opgesteld, waaruit u kunt aflezen met hoeveel decibel een bepaalde versterking correspondeert. In de onderstaande tabel zijn enige veel voorkomende decibel waarden omgerekend naar een spanningsverhouding. Uit deze tabel kunt u aflezen wat er van een ingangsspanning van 1,00 V overblijft als die spanning een bepaald aantal decibel versterkt of verzwakt wordt. Die tweede kolom geeft dan meteen de versterking weer. Als u bij de technische specificaties van een versterker leest dat de versterkingsfactor gelijk is aan +5 dB, dan kunt u uit deze tabel aflezen dat dit overeen komt met een versterking van x1,778.
 |
| Het omrekenen van dB naar de uitgangsspanning bij een ingangsspanning van 1 V. (© 2018 Jos Verstraten) |
Het eerste voordeel is dat grote versterkingen of verzwakkingen teruggebracht worden tot handzame getallen. Verder kunt u de totale versterking van een versterkersysteem nu berekenen door gewoon de verschillende deelversterkingen in dB bij elkaar op te tellen. Dat is een gevolg van de wiskundige theorie die achter het begrip 'logaritme' schuil gaat. In onderstaande figuur is het in een vorige figuur reeds voorgesteld versterkersysteem opnieuw getekend, maar nu met de versterkingen en verzwakkingen weergegeven in dB. De totale versterking volgt uit een eenvoudig optelsommetje
30 dB - 4 dB + 3 dB - 3 dB = 26 dB
Uit de tabel kunt u dan onmiddellijk aflezen dat de totale versterking iets meer bedraagt dan 17,78.
 |
| Dezelfde versterker, maar nu met dB-waarden ingevuld. (© 2018 Jos Verstraten) |
Weergave-karakteristieken
De frequentie-karakteristiek
Bij de beoordeling van de kwaliteit van een analoge versterker of analoog onderdeel speelt de frequentie-karakteristiek een belangrijke rol. Dat is een grafiek waarin u onmiddellijk ziet hoe goed of hoe slecht de versterker of het onderdeel diverse frequenties weergeeft of versterkt. Zo moet een goede audio-versterker in principe alle hoorbare frequenties tussen 10 Hz en 20 kHz even goed weergeven. Zo'n grafiek geeft op de horizontale as de frequentie weer en op de verticale as de versterking. Bij zo'n frequentie/versterking-grafiek komen de geïntroduceerde begrippen 'decibel' en 'logaritme' goed van pas.

Het nut van het begrip 'decibel'
Bij het meten van de versterking van een schakeling bij diverse frequenties is het handig om één bepaalde frequentie als referentie te nemen. Bij audio-schakelingen wordt, bij internationale afspraak, 1 kHz als referentie genomen. Het probleem wordt dan gereduceerd tot het meten van de versterking bij een bepaalde frequentie ten opzichte van de versterking bij de referentie-frequentie van 1 kHz. Kortom, het komt neer op het meten van 'verhoudingen' en is dat begrip nu niet nét een belangrijk gegeven in de definitie van de decibel? De versterking bij 1 kHz wordt dan gelijk gesteld aan 0 dB en de versterking bij alle overige frequenties wordt dan vergeleken met deze 0 dB referentie.
Het nut van het begrip 'logaritme'
Als u de versterking van een audio-versterker wilt meten is het frequentiebereik tussen 20 Hz en 18 kHz niet zo belangrijk. Uit ervaring weten wij dat vrijwel iedere versterker goed presteert in dit bereik. De interessante frequentiegebieden zijn deze onder 20 Hz en deze boven 18 kHz. Laten wij deze gebieden nu eens uitzetten op een lineaire frequentie-as. Dan merkt u dat het zeer interessante blauw weergegeven frequentiegebied onder de 20 Hz nauwelijks zichtbaar is in deze grafiek.
 |
| Het frequentiebereik van 10 Hz tot 20 kHz uitgezet op een lineaire frequentie-as. (© 2018 Jos Verstraten) |
 |
| Het frequentiebereik van 10 Hz tot 20 kHz uitgezet op een logaritmische frequentie-as. (© 2018 Jos Verstraten) |
Dank zij de begrippen 'dB' en 'logaritmische frequentie-as' is het mogelijk de frequentie-weergave van een analoog onderdeel of een analoge schakeling gedetailleerd samen te vatten in één grafiek. In onderstaande grafiek hebben wij bijvoorbeeld de weergave-karakteristiek van de beroemde microfoon SM58 van Shure weergegeven. Zowel zijn gevoeligheid in het laag als in het hoog is duidelijk zichtbaar. Ook in deze grafiek wordt weer 0 dB bij 1 kHz als referentie gebruikt.
 |
| De weergave-karakteristiek van de SM58 microfoon van Shure. (© Shure Distribution Benelux) |
De dB en de sterkte van geluid
Een maatschappelijk probleem
Het kan u niet ontgaan dat de overlast die geluid kan veroorzaken steeds vaker een maatschappelijk discussiepunt vormt. Hoe groot is de geluidsoverlast van Schiphol, van windmolens, van 130 km/h op de snelwegen? In al deze discussies komt het begrip 'decibel' aan de orde.
De geluidsdruk
Geluid nemen wij waar omdat de trommelvliezen in onze oren uiterst gevoelig zijn voor de variaties in luchtdruk. De natuurkundige grootheid druk wordt in de natuurkunde voorgesteld door de grootheid pascal, met als symbool Pa. Ook bij het vergelijken van geluidsdrukken heeft men een referentiedruk ingevoerd en dus komt ook hier het begrip dB aan de orde. De referentie geluidsdruk die een menselijk wezen nog net kan waarnemen is vastgesteld op 2 ● 10−5 Pa bij een referentiefrequentie van (alweer) 1 kHz. Deze geluidsdruk wordt, per definitie, gelijkgesteld aan een geluidsdruk van 0 dB.
De hoorspan
Het menselijk gehoor is extreem gevoelig voor geluidsdrukken en kan bovendien zowel extreem lage als extreem hoge geluidsdrukken waarnemen zonder vast te lopen in ruis (onderkant) of in oversturing (bovenkant). Het totale bereik wordt de 'hoorspan' genoemd en bestrijkt een gebied van 1 op 1.000.000.000.000. Het zal duidelijk zijn dat het bij het verwerken van dergelijke grote verhoudingen alweer voordelig is om gebruik te maken van logaritmische getallen.

De definitie van de decibel bij geluidsdrukken
In formulevorm wordt de effectieve geluidsdruk voorgesteld door de formule
SPLdb = 20 ● log [Peff / Pref]
waarbij de referentiedruk Pref gelijk is aan 2 ● 10−5 Pa.
Internationaal is afgesproken bij het definiëren van geluidsdrukken gebruik te maken van de eenheid SPL, letterwoord van 'Sound Pressure Level'.
Sterktes van geluiden in SPLdB
In de onderstaande figuur hebben wij een aantal geluidsdrukken, waarvan u een bepaalde voorstelling kunt maken, omgerekend naar SPLdb.
Let ook in deze afbeelding op de manier waarop de geluidsdruk op een logaritmische schaal is weergegeven. Dank zij deze schaalindeling kunt u zowel een zeer hoge druk van 20.000 Pa als een zeer lage druk van 0,000.005 Pa goed aflezen.
Let ook op de manier waarop grote getallen worden weergegeven door een aantal dB:
-20 dB = 0,000.002 Pa
0 dB = 0,000.02 Pa
20 dB = 0,000.2 Pa
40 dB = 0,002 Pa
60 dB = 0,02 Pa
80 dB = 0,2 Pa
100 dB = 2 Pa
120 dB = 20 Pa
140 dB = 200 Pa
160 dB = 2.000 Pa
180 dB = 20.000 Pa
 |
| De geluidsdruk in dB van een aantal gebeurtenissen die u zich kunt voorstellen. (© Jurgen Gaeremyn) |
Het begrip dBU
Van 1,000 V naar 0,775 V
In de vorige tabel hebben wij de dB-waarden vergeleken met de referentie 0 dB = 1,000 V. Er bestaat echter nog een tweede reeks dB-waarden, waarbij men als referentie 0 dB = 0,775 V gebruikt. Deze manier van werken wordt voornamelijk toegepast in de professionele audio-wereld. Om geen verwarring te zaaien wordt deze manier van het beschrijven van signaalverhoudingen met decibel's aangeduid met de eenheid dBU. De U staat hierbij voor 'unterminated', niet-belast.
De formule voor de dBU is dus:
dBU = 20 ● log (U / 0,775 V)
Uitwerking van deze formule voor diverse waarden van U levert de onderstaande tabel op.
 |
| Het omrekenen van dBU naar de uitgangsspanning bij een referentiespanning van 0,775 V. (© 2018 Jos Verstraten) |
Een VU-meter is een meter die de sterkte van een geluidssignaal weergeeft in volume units (volume-eenheden). Een dergelijke meter is voorzien van een dBU-schaal, waarbij een uitlezing van 0 VU overeen komt met +4 dBU of een spanning van 1,228 V.
De originele VU-meters zijn analoge meetinstrumenten, dus draaispoelmeters voorzien van een naald die over een schaalverdeling glijdt. Zo'n meter reageert vrij traag op een plotselinge signaalsprong, hetgeen ook de bedoeling is van een VU-meter.
Moderne VU-meters werken met een serie in rij opgestelde LED's, waarbij iedere LED gaat oplichten bij een bepaald aantal VU's op de ingang. Zo'n meter heeft natuurlijk niet de aangeboren trage reactie van een draaispoelmeter. Vandaar dat u de gewenste traagheid elektronisch moet invoeren in het meetsysteem. Zowel de stijgtijd als de daaltijd zijn gestandaardiseerd op 300 ms.
 |
| De schaalindeling in VU's van een standaard analoge VU-meter. (© Iain Fergusson) |
Het klinkt misschien een beetje raar, maar als u audio-signalen in dBU wilt meten hebt u helemaal niets aan de moderne digitale universeelmeters. De elektronica in deze meters kan alleen overweg met lineaire grootheden zoals volt, ampère en ohm. De dB is per definitie geen lineaire grootheid maar een logaritmische grootheid. Als u deze grootheid met een digitale meter zou willen meten, dan moet u een logaritmische versterker te voorschijn toveren. Die bestaan, maar dat zijn ingewikkelde en dure lineaire schakelingen die u bovendien ook nog eens individueel moet afregelen. Niet iets waar een massa-producent vrolijk van wordt!
De oude analoge universeelmeters hadden bijna allemaal wél een dB-schaal, waarmee u audio-signalen in dBU kon meten. Als voorbeeld ziet u in de onderstaande foto de schaal van de oeroude Engelse AVO-meter, met een heel mooie uiteraard niet-lineaire dBU-schaal.
 |
| Met een oeroude analoge universeelmeter kunt u audio-spanningen in dBU meten. (© 2018 Jos Verstraten) |
Analog Circuit Design
