
|
Digitaal naar analoog omzetters, kortweg DAC's genoemd, hebben tot taak een digitale code om te zetten in een analoge spanning. In dit artikel worden de zes belangrijkste principes besproken.

|
Basis principes van DAC's
Vrijwel alles gaat digitaal
Tegenwoordig wordt alles dat wij via elektronische apparatuur horen en zien digitaal gemeten, verwerkt, opgeslagen, verzonden en weer verwerkt. Of het nu de kleuren van een pixel van een foto betreft, het signaal dat een oscilloscoop op zijn scherm zet of het geluid dat uit uw luidsprekers komt, al die gegevens zitten verpakt in een aantal signalen die alleen 'L' of 'H' kunnen zijn. Helaas werken onze zintuigen en hersenen niet digitaal. Die combinatie van lage en hoge signalen moet dus toch weer worden omgezet in een analoog signaal voor het onze zintuigen bereikt.
Dát is de taak van digitaal naar analoog omzetters, kortweg DAC's genoemd naar het Engelse 'Digital to Analog Converter'.
Het 'gewicht' van een digitale code
Een van de belangrijkste begrippen die bij DAC's een rol spelen in het 'gewicht' van de digitale code die aan de DAC wordt aangelegd. In de onderstaande figuur is een digitaal naar analoog omzetter getekend met twee digitale ingangen Qa en Qb. Beide signalen kunnen alleen 'L' of 'H' zijn. Dat betekent dat er vier mogelijke combinaties van 'L' en 'H' signalen kunnen ontstaan. Bij het omzetten van die vier mogelijke binaire combinaties op de ingangen moet een afspraak worden gemaakt met welke analoge spanning op de uitgang iedere combinatie overeen komt.
Zo'n afspraak zou er als volgt kunnen uitzien:
- Qa = 'L', Qb = 'L': analoge uitgangsspanning is gelijk aan 0 V
- Qa = 'H', Qb = 'L': analoge uitgangsspanning is gelijk aan 1 V
- Qa = 'L', Qb = 'H': analoge uitgangsspanning is gelijk aan 2 V
- Qa = 'H', Qb = 'H': analoge uitgangsspanning is gelijk aan 3 V
U kunt dan stellen dat het 'gewicht' van bit Qa gelijk is aan 1 V en het 'gewicht' van bit Qb gelijk is aan 2 V. Het 'gewicht' van de afzonderlijke bits speelt alleen een rol bij het bepalen van het 'gewicht' van de volledige digitale code als het desbetreffende bit 'H' is. Een bit dat 'L' is heeft altijd een gewicht van 0 V.
 |
| Verklaring van het 'gewicht' van een digitale code. (© 2020 Jos Verstraten) |
De macht van twee reeks
In de meeste gevallen worden de gewichtswaarden aan de opeenvolgende bits toegekend volgens de bekende 2n-reeks. Het eerste bit krijgt het gewicht 20 = 1. Het daaropvolgende bit krijgt het gewicht 21 = 2. Het derde bit heeft het gewicht 22 = 4, etc. In het algemeen kunt u stellen dat bij dit soort lineair werkende digitaal naar analoog omzetters het n-de bit een gewicht heeft van 2n.
LSB en MSB
Afgesproken is dat het bit met het laagste gewicht het 'minst significante bit' (LSB) wordt genoemd en het bit met het hoogste gewicht het 'meest significante bit' (MSB).
De relatie tussen de bits
Tussen de bits van zo'n binair werkend 'macht van 2'-systeem bestaat uiteraard een bepaalde relatie. Als alle mogelijke code-combinaties worden doorlopen van totaal gewicht gelijk aan nul tot totaal gewicht gelijk aan de maximale waarde ontstaat een onderling relatie die in de onderstaande figuur is voorgesteld. De vier bits Qa, Qb, Qc en Qd beginnen allemaal in de 'L'-positie: totaal gewicht gelijk aan nul. Bij de eerste code-verandering springt Qa van 'L' naar 'H', zie punt [A]. Bij de tweede code-verandering springt bit Qa weer naar 'L'. Op dat moment gaat bit Qb naar 'H', zie punt [B].
Dat is een algemene eigenschap van dergelijke systemen. Op het moment dat bit Qn van 'H' naar 'L' gaat zal het volgende bit Qn+1 van waarde veranderen. Dat is in de tekening aangegeven met de blauwe pijltjes.
Eigenschap van lineair werkende DAC's
DAC's waarbij de gewichten volgens de beschreven 2n-reeks aan de bits worden toegekend worden lineair werkende DAC's genoemd omdat de analoge uitgangsspanning een bepaald specifiek verloop heeft als u de digitale code aan de ingangen van 'L-L-L-....-L-L' tot en met 'H-H-H-....-H-H' in de normale binaire volgorde laat stijgen. Aan de uitgang ontstaat dan namelijk een trapvormige spanning, die een lineaire zaagtand benadert.
Dit is in de onderstaande figuur getekend voor een systeem dat werkt met vijf bits. Opgemerkt moet worden dat, hoewel de overgrote meerderheid van de leverbare DAC's werkt volgens dit lineaire systeem, er toch ook schakelingen bestaan die van deze regel afwijken. Zo levert Analog Devices bijvoorbeeld een aantal schakelingen waar het verband tussen de gewichten van de digitale codes en de analoge uitgangsspanning logaritmisch verloopt. Dat zijn echter zeer speciale schakelingen en vandaar dat bij het verklaren van de werking van de verschillende DAC-technieken alleen over lineair werkende schakelingen zal worden geschreven.
Werkingsprincipes van lineaire DAC's
Er bestaan zes verschillende werkingsprincipes waarmee het digitale naar analoge proces in lineaire DAC's wordt uitgevoerd:
- De DAC met gewogen weerstanden
- De DAC met een spanning gestuurd R-2R netwerk
- De DAC met een stroom gestuurd R-2R netwerk
- De DAC met geschakelde stroombronnen
- De DAC met dynamic element matching
- De DAC met geïntegreerde variabele pulssturing
Deze zes principes zullen in de volgende hoofdstukken worden verklaard.
Het principe
Bij de DAC met gewogen weerstanden wordt, zie de onderstaande figuur, ieder bit gebruikt voor het besturen van een elektronische omschakelaar. Deze schakelaars S1, S2 en S3 schakelen het moedercontact ofwel aan de massa (GND) ofwel aan een nauwkeurige referentiespanning (Uref). De moedercontacten van de schakelaars zijn verbonden met een weerstand. Alle vrije aansluitingen van deze weerstanden zijn aan elkaar gekoppeld en vormen de uitgang van de schakeling.
De weerstandswaarden zijn niet willekeurig gekozen, maar zijn gewogen. Tussen het gewicht van de bits en het gewicht van de weerstanden bestaat een omgekeerd verband. Het bit met het laagste gewicht bestuurt de elektronische schakelaar van de weerstand met het hoogste gewicht. De onderlinge gewichten van de weerstanden voldoen aan dezelfde 2n-wet als het gewicht van de bits. Als de weerstand met het laagste gewicht een waarde van R heeft, dan zal de weerstand met het hoogste gewicht een waarde van R • 2n hebben.
In het getekende voorbeeld hebben de drie weerstanden dus een waarde van R, 2R en 4R.
Grootte van de analoge uitgangsspanning
Men kan nu aantonen dat als de drie ingangsbits hun normale codevolgorde van 'L-L-L' tot en met 'H-H-H' doorlopen de analoge spanning op de uitgang voldoet aan de eerder gestelde eigenschap van lineair werkende DAC's. Er ontstaat een trapvormige spanning die een lineaire zaagtand benadert.
De elektronische schakelaars schakelen de linker aansluitingen van de weerstanden ofwel naar 0 V ofwel naar +10,000 V, de rechter aansluitingen zijn gemeenschappelijk.
Het komt er dus op neer dat voor iedere codecombinatie een bepaald serie/parallel netwerk van de weerstanden ontstaat. Van ieder netwerk is op een zeer eenvoudige manier de vervangende waarde te berekenen. Voor het getekende voorbeeld kan men berekenen dat de analoge uitgangsspanning voor de verschillende codecombinaties gelijk wordt aan:
0 V
1,428 V
2,857 V
4,285 V
5,714 V
7,142 V
8,571 V
10,000 V
Alle stappen van de stapvormige uitgangsspanning liggen dus precies 1,428 V uit elkaar! Waarmee wordt aangetoond dat de schakeling inderdaad voldoet aan de basiseigenschap van een lineair werkende digitaal naar analoog omzetter.
Uitschakelen van de belastingsinvloed
Bij de besproken schakeling wordt geen rekening gehouden met de invloed van de belasting op de uitgang van de DAC. De interne weerstand van de belasting zal de spanningsdeler van de DAC belasten, waardoor de nauwkeurigheid van de omzetting in het gedrang komt.
Vandaar dat in de praktijk gebruik wordt gemaakt van de schakeling die in de onderstaande figuur wordt voorgesteld. Deze schakeling werkt volgens hetzelfde principe. De weerstanden R, 2R, 4R, ... gaan nu echter naar de inverterende ingang van een operationele versterker. De niet-inverterende ingang van deze schakeling ligt aan de massa.
De schakeling vormt een mengschakeling met virtueel nulpunt. Omdat de niet-inverterende ingang van de op-amp aan de massa ligt zal ook de spanning op de inverterende ingang streven naar 0 V. De gewogen weerstanden leveren nu stromen aan dit punt. Omdat de weerstanden gewogen zijn zullen de stromen dat ook zijn.
Als bit Qa 'H' wordt zal weerstand R1 een stroom van Uref gedeeld door 8R leveren. Het volgende bit Q2 levert een stroom Uref gedeeld door 4R. Deze stroom bedraagt dus het dubbele van de stroom van het LSB.
De stromen die door de bits die 'H' zijn worden geleverd, dus Ia + Ic, kunnen alleen via de terugkoppelingsweerstand Rterug afvloeien. De somstroom wekt over de weerstand een spanningsval op waarvan de grootte uiteraard recht evenredig is met de waarde van de somstroom. Op deze manier ontstaat aan de uitgang van de schakeling een analoge spanning die evenredig is met het gewicht van de digitale code aan de ingang van de schakeling.
Let er echter wél op dat de op-amp een inverterende werking heeft. Op de uitgang ontstaat dus een negatieve zaagtandspanning als de binaire code wordt doorlopen. De somstroom die vanuit de gewogen weerstanden via Rterug naar de uitgang vloeit zorgt er immers voor dat de spanning op de uitgang van de schakeling alleen negatief kan worden.
Nadelen van de DAC met gewogen weerstanden
U zult in de praktijk uitsluitend in de allergoedkoopste apparaten digitaal naar analoog omvormers aantreffen die werken volgens het principe van de gewogen weerstanden. Dat principe heeft immers een aantal nadelen.
Het principe
Het principe van dit soort schakelingen is getekend in de onderstaande figuur. De ingangsbits sturen ook nu elektronische omschakelaars, die weerstanden ofwel met de massa ofwel met een referentiespanning doorverbinden. Het weerstandsnetwerk is echter zeer specifiek gevormd. Met noemt deze structuur een 'laddernetwerk'. Op de eerste plaats worden er slechts twee weerstandswaarden gebruikt, R en 2R. Problemen met uit de hand lopende weerstandswaarden doen zich hier dus niet voor. Op de tweede plaats is de impedantieverhouding veel evenwichtiger. Iedere elektronische schakelaar 'ziet' ongeveer dezelfde impedantie ten opzichte van de massa. De inwendige weerstanden van de elektronische schakelaars hebben dan veel minder invloed op de nauwkeurigheid van de omzetting.
De werking van de schakeling
Uiteraard moet nog bewezen worden dat op de uitgang een trapvormige spanning ontstaat als de codecombinatie op de ingang alle stappen tussen 'L-L-L' en 'H-H-H' doorloopt. Als u er de moeite voor over hebt moet u weer voor iedere ingangscombinatie het equivalent schema van de weerstanden opstellen. Voor iedere code zullen er een aantal weerstanden parallel geschakeld worden tussen de massa en de uitgang en/of tussen de referentiespanning en de uitgang. U kunt dan vaststellen dat inderdaad aan de algemene voorwaarde van een lineair werkende DAC wordt voldaan.
De principiële werking
Het principe van de stroom gestuurde DAC met R-2R weerstanden is getekend in de onderstaande figuur.
De schakeling wordt gekenmerkt door twee uitgangen. Een uitgang Iuit1 vangt de stromen op die worden geleverd door de schakelaars die door hoge bits worden gestuurd. Een tweede uitgang Iuit2 verzamelt de stromen die worden geleverd door de schakelaars die door de lage bits worden gestuurd.
Tot slot is er nog een uitgang Rfb, die u kunt gebruiken voor het omzetten van de uitgangsstromen in een uitgangsspanning. Daarvoor is een operationele versterker nodig, die soms wel en soms niet in de geïntegreerde schakeling van de DAC aanwezig is. De niet-inverterende ingang is verbonden met de massa, de inverterende ingang met de uitgang Iuit1.
Alle stromen die via de 2R-weerstanden worden geleverd vloeien ofwel af naar de massa, ofwel naar de inverterende ingang van de versterker. De somstroom Iuit1 gaat weer via de weerstand Rfb naar de uitgang van de op-amp. Over deze weerstand ontstaat een spanningsval waarvan de grootte wordt gegeven door de som van de stromen die door de weerstand vloeit.
Werking van de schakeling
Ga uit van het gegeven dat de referentiespanning een waarde van 10,00 V heeft en dat de waarde van R gelijk is aan 1 kΩ. U moet bewijzen dat de grootte van de Iuit1 stromen een gewogen waarde hebben. Omdat zowel de inverterende als de niet-inverterende ingang van de operationele versterker op nul staat, kunt u de weerstanden R1 , R3 en R5 naar massa tekenen. Door R1 vloeit een stroom van 5 mA. De spanning over de weerstand is immers gelijk aan de waarde van de referentiespanning (+10,00 V), de weerstand 2R heeft een waarde van 2 kΩ.
Wilt u de waarde van de overige stromen berekenen, dan moet u eerst weten hoe groot de spanningsval is over weerstand R2. De parallel geschakelde weerstanden R5 en R6 kunnen vervangen worden door één weerstand van 1 kΩ. Nadien kunt u R4 en de in serie geschakelde R5/R6 weerstand weer vervangen worden door één weerstand van 2 kΩ. Vervolgens kunt u de parallelschakeling van R3 met R4+R5/R6 vervangen worden door één weerstand van 1 kΩ. Deze vervangingsweerstand staat in serie met R2 geschakeld tussen de referentiespanning en de massa. De totale weerstand van deze kring is 2 kΩ, zodat er een stroom van 5 mA vloeit. Over R2 valt bijgevolg 5 V.
Daaruit volgt dat het knooppunt van R2, R3 en R4 op een spanning staat van +5 V. Door R3 vloeit dus een stroom van 2,5 mA. Omdat R2 5 mA levert en R3 slechts 2,5 mA opneemt, moet de ontbrekende 2,5 mA door R4 afvloeien. Over deze weerstand valt dus een spanning van 2,5 V. U kunt dus besluiten dat er over de weerstanden R5 en R6 ook 2,5 V staat.
U kunt tot slot berekenen dat door de weerstand R5 een stroom van 1,25 mA vloeit.
Als u al deze gegevens op een rijtje zet kunt u besluiten dat de stromen die door R1, R3 en R5 vloeien zich inderdaad gewogen gedragen! Ic is immers gelijk aan 5 mA, Ib gelijk aan 2,5 mA en Ia gelijk aan 1,25 mA. De stromen verhouden zich als 1 tot 2 tot 4, een typische gewogen verhouding die voldoet aan de 2n-wet! De stromen Ia, Ib en Ic vloeien alleen maar naar de inverterende ingang van de operationele versterker als de schakelaars gestuurd worden door bits die 'H' zijn. In het andere geval vloeien de stromen rechtstreeks al naar de massa. De som van de gewogen stromen vloeit door de weerstand Rfb en wordt daarin uiteraard omgezet in een gewogen spanning.

Voordelen van de stroom gestuurde R-2R schakeling
Het principe van het stroom gestuurde R-2R netwerk heeft zoveel voordelen dat de meeste geïntegreerde DAC's volgens dit systeem werken. Op de eerste plaats hoeft men maar twee weerstandswaarden in het IC te integreren, hetgeen zeer eenvoudig mogelijk is met behoud van zeer kleine toleranties. Op de tweede plaats kunnen de weerstanden een vrij lage waarde hebben, hetgeen het integratie-proces nog gemakkelijker maakt. Op de derde plaats is de uitgangsspanning van de schakeling belastingsonafhankelijk. De actieve stroom naar spanning omzetter met behulp van de operationele versterker heeft zelf al een zeer lage uitgangsimpedantie, maar zal iedere afwijking van de ideale uitgangsspanning onmiddellijk dank zij zijn zeer hoge versterking compenseren.
Een praktische schakeling met een AD7523
In de onderstaande figuur is een praktische schakeling getekend van een DAC die volgens het beschreven principe werkt. De schakeling maakt gebruik van een DAC van het type AD7523 en een willekeurige operationele versterker. De AD7523 is een oudgediende van Analog Devices die voor iets minder dan twee euro via de bekende Chinese shops te koop is.
De schakeling kan geijkt worden door de weerstand R1, in serie geschakeld tussen de referentiespanning en de referentie-ingang van het IC, te verdraaien. U maakt alle bits 'H' en stelt de weerstand in tot de analoge uitgangsspanning gelijk is aan de maximale waarde die u wilt hebben.
De interne schakeling van de AD7523 bevat niets meer maar ook niets minder dan het principiële schema van de bovenstaande figuur.
De principiële werking
Het interne schema en de noodzakelijke externe schakelingen van een DAC met geschakelde stroombronnen is getekend in de onderstaande figuur. De schakeling in het IC zélf bestaat uit drie delen:
Het genereren van de vier gewogen stromen
De interne transistor T1 wordt opgenomen in een externe zeer nauwkeurige stroombron. In het schema is deze bron samengesteld uit een operationele versterker en een zenerdiode. Deze schakeling stuurt een zeer nauwkeurige stroom Iref van 125 μA naar de collector van T1.
De basis van T1 is rechtstreeks verbonden met de basissen van de vier stroomversterkers T2 tot en met T5. Deze lijn noemt men de 'common base line'. De vijf transistoren hebben, als gevolg van het integratieproces, volledig identieke eigenschappen. Tussen de respectievelijke emitters en de negatieve voeding -Ub staan vier weerstanden die een gewogen waarde hebben (verhouding is gelijk aan 1/2/4/8). Bovendien is de grootste van deze weerstanden gelijk aan de emitterweerstand van T1. Omdat alle transistoren op dezelfde basisspanning staan en bovendien identieke basis/emitter-spanningen hebben (gelijke eigenschappen!) staan over alle weerstanden gelijke spanningen.
Het gevolg is dat door de transistoren stromen vloeien die gelijk zijn aan respectievelijk lxIref, 2xIref, 4xIref en 8xIref. Deze stroomverhouding is volledig en uitsluitend afhankelijk van nauwkeurigheid van de weerstanden!
De collectoren van T2 tot en met T5 zijn verbonden met de uitgangslijn Iuit. Door deze lijn zal dus de totale somstroom vloeien van alle geleidende transistoren. Het al dan niet geleiden van deze transistoren wordt gecontroleerd door de schakeltrappen in het besturingsblok.
Bij het doorlopen van de digitale code van 'L-L-L-L' naar 'H-H-H-H' wordt de uitgangsstroom Iuit in zestien trappen ingesteld tussen 0 en 15xIref. Deze stroom kan met de operationele versterker worden omgezet in een gewogen uitgangsspanning.
Inleiding
In feite zijn de besproken systemen te beschouwen als een samenstelling van een aantal stroombronnen die stromen leveren met een onderlinge verhouding van Iref tot 2xIref tot 4xIref tot 8xIref enzoverder.
Als het aantal bits toeneemt zal ook de verhouding tussen de laagste en de hoogste stroom erg toenemen. Bij een acht bit systeem bestaat er reeds een stroomverhouding tussen de kleinste en de grootste stroom van 1 op 256! Als het aantal te verwerken bits stijgt, krijgt men problemen met de tolerantie op de weerstanden. Deze afwijkingen bepalen immers in zeer grote mate de onderlinge verhouding van de stromen. Fouten op de weerstandswaarden komen tot uiting in fouten in de stroomverdeling.
Dat gegeven heeft ontwerpers op het idee gebracht niet even veel verschillende stroombronnen in de DAC in te bouwen als er bits te verwerken zijn, maar slechts één. De stroom van deze bron wordt door speciale schakelingen steeds opnieuw heel precies door twee gedeeld, zodat uiteindelijk toch de juiste stroomverhoudingen ontstaan.
Dit principe wordt door de ontwerpers 'Dynamic Element Matching' (DEM) genoemd.
Principe van Dynamic Element Matching
Het principe van deze techniek is geschetst in de onderstaande figuur. Een stroombron Icte levert een stroom aan twee identieke weerstanden R. Natuurlijk zijn deze weerstanden niet echt identiek, omdat deze onderdelen ieder geteisterd worden door een bepaalde tolerantie ±ΔR.
De stroom I van de stroombron zal dus omgekeerd evenredig met de reële waarde van de weerstanden over beide ketens verdeeld worden. De twee niet gelijke stromen die door de weerstanden vloeien worden door middel van twee elektronische schakelaars snel heen en weer geschakeld tussen de twee uitgangen van de schakeling. Dat heen en weer schakelen moet met een duty-cycle van precies 50 % gebeuren. Technisch is dat geen probleem omdat men de schakelaars kan sturen uit de uitgangen van een geclockte type-JK flip-flop. Deze levert per definitie een mooie symmetrische uitgangspuls.
Het zal nu duidelijk zijn dat de gemiddelde stromen die naar de uitgangen stromen heel nauwkeurig aan elkaar gelijk zijn. De linker stroom bestaan immers voor 50 % uit de stroom die door de linker weerstand wordt geleverd en voor 50 % uit de stroom die door de rechter weerstand wordt geleverd. Voor de rechter uitgang geldt precies hetzelfde.
Het volstaat de twee stromen door middel van condensatoren te middelen om twee gelijkstromen te verkrijgen die heel nauwkeurig aan elkaar gelijk zijn. Het probleem is verlegd naar het openen en sluiten van elektronische schakelaars met een duty-cycle van precies 50 %. Een digitaal probleem dat zonder moeilijkheden is op te lossen als de schakelfrequentie niet te hoog is.
Meerdere bits
Met één DEM-schakeling kan men een stroom 2.I omzetten in twee stromen 1.I. Door diverse identieke schakelingen te cascaderen volgens het rechter schema kan men uit de ene basis stroombron 2.I stromen genereren van 1.I, ½.I, ¼.I, etc.
Praktische schakelingen
In de praktische DEM-schakelingen wordt het principe verder uitgewerkt. Een stroom 4.l wordt nu door een ingewikkelder schakelaarsysteem omgezet in drie stromen van respectievelijk 1.I, 1.I en 2.I.
Een van de stromen 1.I wordt dan weer gebruikt als basis voor het volgende element uit de gecascadeerde keten, zodat stromen van ¼.I, ¼.I en ½.I ontstaan.
Principe van het systeem
Andere fabrikanten hebben een ander alternatief ontwikkeld voor het stroom gestuurde R-2R systeem. Er wordt, net zoals bij het vorige systeem, uitgegaan van slechts één stroombron. Het basisprincipe van het systeem, voor de eenvoud toegepast op een vier bit systeem, is getekend links in de onderstaande figuur. De stroombron Icte is via een elektronische schakelaar S1 aangesloten op een integrator. Als een integrator gestuurd wordt met een constante stroom, dan zal de uitgangsspanning van de schakeling een lineair stijgende spanning zijn waarvan de stijgtijd evenredig is met de grootte van de constante stroom.
De binaire code op de ingangen wordt door een timer omgezet in een eenmalige pulstrein. Het aantal pulsjes in deze trein is gelijk aan het binaire gewicht van de digitale code. Als de code 'L-L-L-L' is levert de timer géén pulsjes. Is de code gelijk aan 'L-L-L-H' dan zal de timer één smal pulsje leveren dat de schakelaar S1 even sluit. Is de code gelijk aan 'H-H-L-H' dan levert de timer, zie rechts in de bovenstaande figuur, een pulstrein die is samengesteld uit 12 pulsjes.
De uitgangsspanning Uanaloog zal nu recht evenredig zijn met het aantal pulsjes in de pulstrein, daar zorgt de integrator wel voor. Zorgen 15 pulsjes voor een uitgangsspanning van 150 mV dan zal een pulstrein met slechts 7 pulsjes een analoge uitgangsspanning van 70 mV tot gevolg hebben. Het analoge probleem van de nauwkeurigheid van de stroombron(nen) wordt ook nu handig omzeild en verlegd naar een digitaal probleem, namelijk zet de binaire code op de ingangen om in een pulstrein. Een probleem dat zonder enige onnauwkeurigheid opgelost kan worden!
Sample-and-hold noodzakelijk
Op de uitgang verschijnt gedurende de digitaal naar analoog omzetting een trapvormig verlopende spanning. Alleen de eindwaarde van deze spanning is echter van belang. Het zal duidelijk zijn dat het noodzakelijk is deze eindwaarde na het omzettingsproces te bewaren in een sample-and-hold schakeling (S&H). Nadat de volgende conversie is voltooid is volstaat het de nieuwe topwaarde van de trapvormige spanning weer in de S&H in te lezen.
Over sample-and-hold schakelingen is op dit blog een eigen artikel geschreven, lees: Componenten: sample and hold.
Voor- en nadelen van het systeem
Enig bezwaar van de schakeling is dat de frequentie van de pulsjes uit de pulstrein gelijk moet zijn aan het aantal codecombinaties dat de digitale ingangscode kan bevatten, vermenigvuldigd met het aantal codecombinaties dat per seconde aan de DAC wordt aangelegd.
Voordeel is echter dat de schakeling absoluut geen last heeft van glitches (lees verder), dit vanwege de integrator en de noodzakelijke sample and hold.
Inleiding
Een verhaal over digitaal naar analoog omzetting kan niet geschreven worden zonder aandacht te besteden aan het verschijnsel 'glitching'. Een fundamenteel probleem bij alle schakelaar gestuurde digitaal naar analoog omzetters is dat er gedurende de overgang van de ene naar de volgende ingangscode op de analoge uitgang van de schakeling korte, onvoorspelbare stoorpulsen ontstaan. Deze pulsen worden 'glitches' genoemd en deze storingen moeten in de meeste gevallen uit het analoge signaal worden verwijderd.

Het ontstaan van glitches
Glitches ontstaan doordat niet alle elektronische stroomschakelaars in de DAC even snel van de ene naar de andere toestand schakelen. Bij het aanpassen van de analoge uitgangsspanning aan een nieuwe digitale code op de ingangen zal in het gunstigste geval slechts één schakelaar van stand verwisselen. Het kan echter ook zijn dat alle schakelaars moeten omschakelen.
Het gevolg is dat de glitches niet allemaal even groot en breed zijn. Een onregelmatig stoorsignaal heeft een zeer brede bandbreedte en is dus rijk aan harmonischen. Bij audio-toepassingen zullen de glitches zorgen voor een typisch ruisgeluid dat met de bekende filtertechnieken nauwelijks is te onderdrukken.
In de onderstaande figuur is de situatie geschetst die bij een acht bit brede DAC ontstaat als de ingangscode omschakelt van 'L-H-H-H-H-H-H-H' naar 'H-L-L-L-L-L-L-L'. Op dat moment doet zich, althans wat glitches betreft, de slechtst mogelijke situatie voor omdat alle stroombron schakelaars in de DAC moeten omschakelen. Nu werken deze schakelaars niet even snel. Het kan dus gebeuren dat eerst de schakelaar van het MSB omschakelt, waardoor het lijkt alsof de digitale code even gelijk wordt aan 'H-H-H-H-H-H-H-H'. De analoge uitgang zal naar de hoge spanning willen schakelen die overeen komt met deze code. De uitgangsspanning van de DAC gaat dus plotseling stijgen. Alvorens echter de eindwaarde van deze foutieve code is bereikt zullen ook de andere stroombron schakelaars omgeschakeld zijn. De analoge uitgang gaat dan terug dalen naar de waarde die overeen komt met de nieuwe ingangscode. Op de uitgang ontstaat dus een zeer smalle positieve piek, een positieve glitch.
Als echter de MSB-schakelaar als laatste omschakelt ontstaat even een situatie waarbij het lijkt alsof de ingangscode gelijk is aan 'L-L-L-L-L-L-L-L'. Op dezelfde manier kunt u aantonen dat er nu een negatieve glitch ontstaat.
Het tijdsinterval waarin deze verschijnselen zich afspelen wordt de 'skew tijd' genoemd.
LSB en MSB
Afgesproken is dat het bit met het laagste gewicht het 'minst significante bit' (LSB) wordt genoemd en het bit met het hoogste gewicht het 'meest significante bit' (MSB).
De relatie tussen de bits
Tussen de bits van zo'n binair werkend 'macht van 2'-systeem bestaat uiteraard een bepaalde relatie. Als alle mogelijke code-combinaties worden doorlopen van totaal gewicht gelijk aan nul tot totaal gewicht gelijk aan de maximale waarde ontstaat een onderling relatie die in de onderstaande figuur is voorgesteld. De vier bits Qa, Qb, Qc en Qd beginnen allemaal in de 'L'-positie: totaal gewicht gelijk aan nul. Bij de eerste code-verandering springt Qa van 'L' naar 'H', zie punt [A]. Bij de tweede code-verandering springt bit Qa weer naar 'L'. Op dat moment gaat bit Qb naar 'H', zie punt [B].
Dat is een algemene eigenschap van dergelijke systemen. Op het moment dat bit Qn van 'H' naar 'L' gaat zal het volgende bit Qn+1 van waarde veranderen. Dat is in de tekening aangegeven met de blauwe pijltjes.
 |
| De relatie tussen de bits in een 'macht van 2'-systeem. (© 2020 Jos Verstraten) |
Eigenschap van lineair werkende DAC's
DAC's waarbij de gewichten volgens de beschreven 2n-reeks aan de bits worden toegekend worden lineair werkende DAC's genoemd omdat de analoge uitgangsspanning een bepaald specifiek verloop heeft als u de digitale code aan de ingangen van 'L-L-L-....-L-L' tot en met 'H-H-H-....-H-H' in de normale binaire volgorde laat stijgen. Aan de uitgang ontstaat dan namelijk een trapvormige spanning, die een lineaire zaagtand benadert.
Dit is in de onderstaande figuur getekend voor een systeem dat werkt met vijf bits. Opgemerkt moet worden dat, hoewel de overgrote meerderheid van de leverbare DAC's werkt volgens dit lineaire systeem, er toch ook schakelingen bestaan die van deze regel afwijken. Zo levert Analog Devices bijvoorbeeld een aantal schakelingen waar het verband tussen de gewichten van de digitale codes en de analoge uitgangsspanning logaritmisch verloopt. Dat zijn echter zeer speciale schakelingen en vandaar dat bij het verklaren van de werking van de verschillende DAC-technieken alleen over lineair werkende schakelingen zal worden geschreven.
 |
| De specifieke vorm van de analoge uitgangsspanning van een lineaire DAC. (© 2020 Jos Verstraten) |
Werkingsprincipes van lineaire DAC's
Er bestaan zes verschillende werkingsprincipes waarmee het digitale naar analoge proces in lineaire DAC's wordt uitgevoerd:
- De DAC met gewogen weerstanden
- De DAC met een spanning gestuurd R-2R netwerk
- De DAC met een stroom gestuurd R-2R netwerk
- De DAC met geschakelde stroombronnen
- De DAC met dynamic element matching
- De DAC met geïntegreerde variabele pulssturing
Deze zes principes zullen in de volgende hoofdstukken worden verklaard.
De DAC met gewogen weerstanden
Het principe
Bij de DAC met gewogen weerstanden wordt, zie de onderstaande figuur, ieder bit gebruikt voor het besturen van een elektronische omschakelaar. Deze schakelaars S1, S2 en S3 schakelen het moedercontact ofwel aan de massa (GND) ofwel aan een nauwkeurige referentiespanning (Uref). De moedercontacten van de schakelaars zijn verbonden met een weerstand. Alle vrije aansluitingen van deze weerstanden zijn aan elkaar gekoppeld en vormen de uitgang van de schakeling.
De weerstandswaarden zijn niet willekeurig gekozen, maar zijn gewogen. Tussen het gewicht van de bits en het gewicht van de weerstanden bestaat een omgekeerd verband. Het bit met het laagste gewicht bestuurt de elektronische schakelaar van de weerstand met het hoogste gewicht. De onderlinge gewichten van de weerstanden voldoen aan dezelfde 2n-wet als het gewicht van de bits. Als de weerstand met het laagste gewicht een waarde van R heeft, dan zal de weerstand met het hoogste gewicht een waarde van R • 2n hebben.
In het getekende voorbeeld hebben de drie weerstanden dus een waarde van R, 2R en 4R.
 |
| Het principe van een DAC met gewogen weerstanden. (© 2020 Jos Verstraten) |
Grootte van de analoge uitgangsspanning
Men kan nu aantonen dat als de drie ingangsbits hun normale codevolgorde van 'L-L-L' tot en met 'H-H-H' doorlopen de analoge spanning op de uitgang voldoet aan de eerder gestelde eigenschap van lineair werkende DAC's. Er ontstaat een trapvormige spanning die een lineaire zaagtand benadert.
De elektronische schakelaars schakelen de linker aansluitingen van de weerstanden ofwel naar 0 V ofwel naar +10,000 V, de rechter aansluitingen zijn gemeenschappelijk.
Het komt er dus op neer dat voor iedere codecombinatie een bepaald serie/parallel netwerk van de weerstanden ontstaat. Van ieder netwerk is op een zeer eenvoudige manier de vervangende waarde te berekenen. Voor het getekende voorbeeld kan men berekenen dat de analoge uitgangsspanning voor de verschillende codecombinaties gelijk wordt aan:
0 V
1,428 V
2,857 V
4,285 V
5,714 V
7,142 V
8,571 V
10,000 V
Alle stappen van de stapvormige uitgangsspanning liggen dus precies 1,428 V uit elkaar! Waarmee wordt aangetoond dat de schakeling inderdaad voldoet aan de basiseigenschap van een lineair werkende digitaal naar analoog omzetter.
Uitschakelen van de belastingsinvloed
Bij de besproken schakeling wordt geen rekening gehouden met de invloed van de belasting op de uitgang van de DAC. De interne weerstand van de belasting zal de spanningsdeler van de DAC belasten, waardoor de nauwkeurigheid van de omzetting in het gedrang komt.
Vandaar dat in de praktijk gebruik wordt gemaakt van de schakeling die in de onderstaande figuur wordt voorgesteld. Deze schakeling werkt volgens hetzelfde principe. De weerstanden R, 2R, 4R, ... gaan nu echter naar de inverterende ingang van een operationele versterker. De niet-inverterende ingang van deze schakeling ligt aan de massa.
De schakeling vormt een mengschakeling met virtueel nulpunt. Omdat de niet-inverterende ingang van de op-amp aan de massa ligt zal ook de spanning op de inverterende ingang streven naar 0 V. De gewogen weerstanden leveren nu stromen aan dit punt. Omdat de weerstanden gewogen zijn zullen de stromen dat ook zijn.
Als bit Qa 'H' wordt zal weerstand R1 een stroom van Uref gedeeld door 8R leveren. Het volgende bit Q2 levert een stroom Uref gedeeld door 4R. Deze stroom bedraagt dus het dubbele van de stroom van het LSB.
De stromen die door de bits die 'H' zijn worden geleverd, dus Ia + Ic, kunnen alleen via de terugkoppelingsweerstand Rterug afvloeien. De somstroom wekt over de weerstand een spanningsval op waarvan de grootte uiteraard recht evenredig is met de waarde van de somstroom. Op deze manier ontstaat aan de uitgang van de schakeling een analoge spanning die evenredig is met het gewicht van de digitale code aan de ingang van de schakeling.
Let er echter wél op dat de op-amp een inverterende werking heeft. Op de uitgang ontstaat dus een negatieve zaagtandspanning als de binaire code wordt doorlopen. De somstroom die vanuit de gewogen weerstanden via Rterug naar de uitgang vloeit zorgt er immers voor dat de spanning op de uitgang van de schakeling alleen negatief kan worden.
 |
| Stroombronschakeling van een DAC met gewogen weerstanden. (© 2020 Jos Verstraten) |
Nadelen van de DAC met gewogen weerstanden
U zult in de praktijk uitsluitend in de allergoedkoopste apparaten digitaal naar analoog omvormers aantreffen die werken volgens het principe van de gewogen weerstanden. Dat principe heeft immers een aantal nadelen.
- Op de eerste plaats moet u gebruik maken van weerstanden met een zeer hoge waarde als het aantal bits van de omzetter stijgt. Om de invloed van de interne weerstand van de elektronische schakelaars te minimaliseren moet u met een basisweerstand bij het MSB van minstens 30 kΩ werken. Bij een acht bit DAC hebt u bij het LSB al een weerstand van bijna 4 MΩ nodig!
- Op de tweede plaats hangt de nauwkeurigheid van de omzetting af van de tolerantie op de weerstanden. In feite kunt u zelfs bij de acht bit brede schakeling al geen 1 % weerstanden toepassen! Nu is het een feit dat bij alle principes nauwkeurige weerstanden vereist zijn. Zoals uit de volgende hoofdstukken zal blijken hebt u bij de andere principes echter te maken met identieke weerstanden. Het is technologisch tamelijk eenvoudig om een aantal identieke weerstanden met zeer kleine toleranties op een chip te integreren.
- Op de derde plaats heeft de besproken schakeling een zeer grote uitgangsimpedantie, dit vanwege de hoge weerstandswaarden die bij de omzetting een rol spelen. Deze hoge weerstanden vormen, samen met de onvermijdelijke bedradingscapaciteiten, laagdoorlaat filtertjes die de werking van de schakeling bij het verwerken van snelle veranderingen in de digitale code zeer nadelig beïnvloeden.
De DAC met een spanning gestuurd R-2R netwerk
Het principe
Het principe van dit soort schakelingen is getekend in de onderstaande figuur. De ingangsbits sturen ook nu elektronische omschakelaars, die weerstanden ofwel met de massa ofwel met een referentiespanning doorverbinden. Het weerstandsnetwerk is echter zeer specifiek gevormd. Met noemt deze structuur een 'laddernetwerk'. Op de eerste plaats worden er slechts twee weerstandswaarden gebruikt, R en 2R. Problemen met uit de hand lopende weerstandswaarden doen zich hier dus niet voor. Op de tweede plaats is de impedantieverhouding veel evenwichtiger. Iedere elektronische schakelaar 'ziet' ongeveer dezelfde impedantie ten opzichte van de massa. De inwendige weerstanden van de elektronische schakelaars hebben dan veel minder invloed op de nauwkeurigheid van de omzetting.
 |
| Het principe van de DAC met spanning gestuurd R-2R netwerk. (© 2020 Jos Verstraten) |
De werking van de schakeling
Uiteraard moet nog bewezen worden dat op de uitgang een trapvormige spanning ontstaat als de codecombinatie op de ingang alle stappen tussen 'L-L-L' en 'H-H-H' doorloopt. Als u er de moeite voor over hebt moet u weer voor iedere ingangscombinatie het equivalent schema van de weerstanden opstellen. Voor iedere code zullen er een aantal weerstanden parallel geschakeld worden tussen de massa en de uitgang en/of tussen de referentiespanning en de uitgang. U kunt dan vaststellen dat inderdaad aan de algemene voorwaarde van een lineair werkende DAC wordt voldaan.
De DAC met een stroom gestuurd R-2R netwerk
De principiële werking
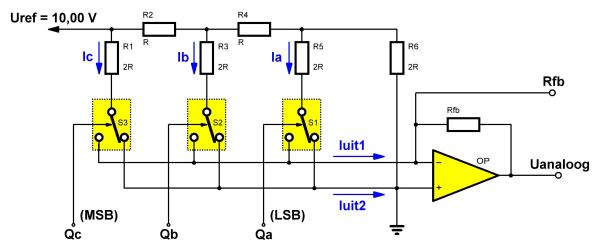
Het principe van de stroom gestuurde DAC met R-2R weerstanden is getekend in de onderstaande figuur.
De schakeling wordt gekenmerkt door twee uitgangen. Een uitgang Iuit1 vangt de stromen op die worden geleverd door de schakelaars die door hoge bits worden gestuurd. Een tweede uitgang Iuit2 verzamelt de stromen die worden geleverd door de schakelaars die door de lage bits worden gestuurd.
Tot slot is er nog een uitgang Rfb, die u kunt gebruiken voor het omzetten van de uitgangsstromen in een uitgangsspanning. Daarvoor is een operationele versterker nodig, die soms wel en soms niet in de geïntegreerde schakeling van de DAC aanwezig is. De niet-inverterende ingang is verbonden met de massa, de inverterende ingang met de uitgang Iuit1.
Alle stromen die via de 2R-weerstanden worden geleverd vloeien ofwel af naar de massa, ofwel naar de inverterende ingang van de versterker. De somstroom Iuit1 gaat weer via de weerstand Rfb naar de uitgang van de op-amp. Over deze weerstand ontstaat een spanningsval waarvan de grootte wordt gegeven door de som van de stromen die door de weerstand vloeit.
 |
| Het principe van de DAC met stroom gestuurd R-2R netwerk. (© 2020 Jos Verstraten) |
Werking van de schakeling
Ga uit van het gegeven dat de referentiespanning een waarde van 10,00 V heeft en dat de waarde van R gelijk is aan 1 kΩ. U moet bewijzen dat de grootte van de Iuit1 stromen een gewogen waarde hebben. Omdat zowel de inverterende als de niet-inverterende ingang van de operationele versterker op nul staat, kunt u de weerstanden R1 , R3 en R5 naar massa tekenen. Door R1 vloeit een stroom van 5 mA. De spanning over de weerstand is immers gelijk aan de waarde van de referentiespanning (+10,00 V), de weerstand 2R heeft een waarde van 2 kΩ.
Wilt u de waarde van de overige stromen berekenen, dan moet u eerst weten hoe groot de spanningsval is over weerstand R2. De parallel geschakelde weerstanden R5 en R6 kunnen vervangen worden door één weerstand van 1 kΩ. Nadien kunt u R4 en de in serie geschakelde R5/R6 weerstand weer vervangen worden door één weerstand van 2 kΩ. Vervolgens kunt u de parallelschakeling van R3 met R4+R5/R6 vervangen worden door één weerstand van 1 kΩ. Deze vervangingsweerstand staat in serie met R2 geschakeld tussen de referentiespanning en de massa. De totale weerstand van deze kring is 2 kΩ, zodat er een stroom van 5 mA vloeit. Over R2 valt bijgevolg 5 V.
Daaruit volgt dat het knooppunt van R2, R3 en R4 op een spanning staat van +5 V. Door R3 vloeit dus een stroom van 2,5 mA. Omdat R2 5 mA levert en R3 slechts 2,5 mA opneemt, moet de ontbrekende 2,5 mA door R4 afvloeien. Over deze weerstand valt dus een spanning van 2,5 V. U kunt dus besluiten dat er over de weerstanden R5 en R6 ook 2,5 V staat.
U kunt tot slot berekenen dat door de weerstand R5 een stroom van 1,25 mA vloeit.
Als u al deze gegevens op een rijtje zet kunt u besluiten dat de stromen die door R1, R3 en R5 vloeien zich inderdaad gewogen gedragen! Ic is immers gelijk aan 5 mA, Ib gelijk aan 2,5 mA en Ia gelijk aan 1,25 mA. De stromen verhouden zich als 1 tot 2 tot 4, een typische gewogen verhouding die voldoet aan de 2n-wet! De stromen Ia, Ib en Ic vloeien alleen maar naar de inverterende ingang van de operationele versterker als de schakelaars gestuurd worden door bits die 'H' zijn. In het andere geval vloeien de stromen rechtstreeks al naar de massa. De som van de gewogen stromen vloeit door de weerstand Rfb en wordt daarin uiteraard omgezet in een gewogen spanning.

Voordelen van de stroom gestuurde R-2R schakeling
Het principe van het stroom gestuurde R-2R netwerk heeft zoveel voordelen dat de meeste geïntegreerde DAC's volgens dit systeem werken. Op de eerste plaats hoeft men maar twee weerstandswaarden in het IC te integreren, hetgeen zeer eenvoudig mogelijk is met behoud van zeer kleine toleranties. Op de tweede plaats kunnen de weerstanden een vrij lage waarde hebben, hetgeen het integratie-proces nog gemakkelijker maakt. Op de derde plaats is de uitgangsspanning van de schakeling belastingsonafhankelijk. De actieve stroom naar spanning omzetter met behulp van de operationele versterker heeft zelf al een zeer lage uitgangsimpedantie, maar zal iedere afwijking van de ideale uitgangsspanning onmiddellijk dank zij zijn zeer hoge versterking compenseren.
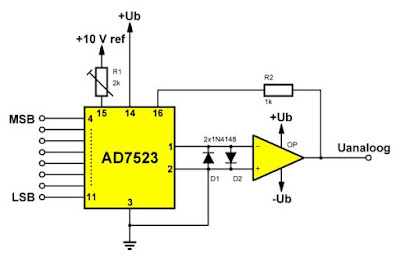
Een praktische schakeling met een AD7523
In de onderstaande figuur is een praktische schakeling getekend van een DAC die volgens het beschreven principe werkt. De schakeling maakt gebruik van een DAC van het type AD7523 en een willekeurige operationele versterker. De AD7523 is een oudgediende van Analog Devices die voor iets minder dan twee euro via de bekende Chinese shops te koop is.
De schakeling kan geijkt worden door de weerstand R1, in serie geschakeld tussen de referentiespanning en de referentie-ingang van het IC, te verdraaien. U maakt alle bits 'H' en stelt de weerstand in tot de analoge uitgangsspanning gelijk is aan de maximale waarde die u wilt hebben.
De interne schakeling van de AD7523 bevat niets meer maar ook niets minder dan het principiële schema van de bovenstaande figuur.
 |
| Praktische schakeling van een DAC die werkt volgens het stroom gestuurde R-2R principe. (© 2020 Jos Verstraten) |
De DAC met geschakelde stroombronnen
De principiële werking
Het interne schema en de noodzakelijke externe schakelingen van een DAC met geschakelde stroombronnen is getekend in de onderstaande figuur. De schakeling in het IC zélf bestaat uit drie delen:
- Een zeer nauwkeurige stroombron met als actief element transistor T1.
- Vier stroomversterkers rond de transistoren T2, T3, T4 en T5 die de referentiestroom van T1 versterken tot 1x, 2x, 4x en 8x de basiswaarde.
- Vier logische schakelaars in het blok 'BESTURING' die de stromen van de vier stroomversterkers op bevel van de binaire code naar de stroomuitgang Iuit schakelen.
 |
| Intern schema van een geschakelde stroombron DAC met de noodzakelijke externe in- en uitgangsschakelingen. (© 2020 Jos Verstraten) |
Het genereren van de vier gewogen stromen
De interne transistor T1 wordt opgenomen in een externe zeer nauwkeurige stroombron. In het schema is deze bron samengesteld uit een operationele versterker en een zenerdiode. Deze schakeling stuurt een zeer nauwkeurige stroom Iref van 125 μA naar de collector van T1.
De basis van T1 is rechtstreeks verbonden met de basissen van de vier stroomversterkers T2 tot en met T5. Deze lijn noemt men de 'common base line'. De vijf transistoren hebben, als gevolg van het integratieproces, volledig identieke eigenschappen. Tussen de respectievelijke emitters en de negatieve voeding -Ub staan vier weerstanden die een gewogen waarde hebben (verhouding is gelijk aan 1/2/4/8). Bovendien is de grootste van deze weerstanden gelijk aan de emitterweerstand van T1. Omdat alle transistoren op dezelfde basisspanning staan en bovendien identieke basis/emitter-spanningen hebben (gelijke eigenschappen!) staan over alle weerstanden gelijke spanningen.
Het gevolg is dat door de transistoren stromen vloeien die gelijk zijn aan respectievelijk lxIref, 2xIref, 4xIref en 8xIref. Deze stroomverhouding is volledig en uitsluitend afhankelijk van nauwkeurigheid van de weerstanden!
De collectoren van T2 tot en met T5 zijn verbonden met de uitgangslijn Iuit. Door deze lijn zal dus de totale somstroom vloeien van alle geleidende transistoren. Het al dan niet geleiden van deze transistoren wordt gecontroleerd door de schakeltrappen in het besturingsblok.
Bij het doorlopen van de digitale code van 'L-L-L-L' naar 'H-H-H-H' wordt de uitgangsstroom Iuit in zestien trappen ingesteld tussen 0 en 15xIref. Deze stroom kan met de operationele versterker worden omgezet in een gewogen uitgangsspanning.
De DAC met dynamic element matching
Inleiding
In feite zijn de besproken systemen te beschouwen als een samenstelling van een aantal stroombronnen die stromen leveren met een onderlinge verhouding van Iref tot 2xIref tot 4xIref tot 8xIref enzoverder.
Als het aantal bits toeneemt zal ook de verhouding tussen de laagste en de hoogste stroom erg toenemen. Bij een acht bit systeem bestaat er reeds een stroomverhouding tussen de kleinste en de grootste stroom van 1 op 256! Als het aantal te verwerken bits stijgt, krijgt men problemen met de tolerantie op de weerstanden. Deze afwijkingen bepalen immers in zeer grote mate de onderlinge verhouding van de stromen. Fouten op de weerstandswaarden komen tot uiting in fouten in de stroomverdeling.
Dat gegeven heeft ontwerpers op het idee gebracht niet even veel verschillende stroombronnen in de DAC in te bouwen als er bits te verwerken zijn, maar slechts één. De stroom van deze bron wordt door speciale schakelingen steeds opnieuw heel precies door twee gedeeld, zodat uiteindelijk toch de juiste stroomverhoudingen ontstaan.
Dit principe wordt door de ontwerpers 'Dynamic Element Matching' (DEM) genoemd.
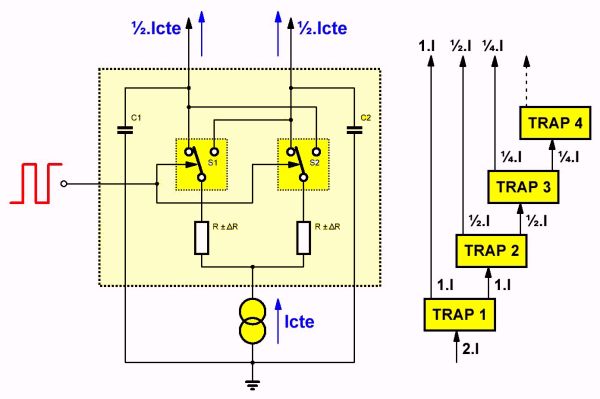
Principe van Dynamic Element Matching
Het principe van deze techniek is geschetst in de onderstaande figuur. Een stroombron Icte levert een stroom aan twee identieke weerstanden R. Natuurlijk zijn deze weerstanden niet echt identiek, omdat deze onderdelen ieder geteisterd worden door een bepaalde tolerantie ±ΔR.
De stroom I van de stroombron zal dus omgekeerd evenredig met de reële waarde van de weerstanden over beide ketens verdeeld worden. De twee niet gelijke stromen die door de weerstanden vloeien worden door middel van twee elektronische schakelaars snel heen en weer geschakeld tussen de twee uitgangen van de schakeling. Dat heen en weer schakelen moet met een duty-cycle van precies 50 % gebeuren. Technisch is dat geen probleem omdat men de schakelaars kan sturen uit de uitgangen van een geclockte type-JK flip-flop. Deze levert per definitie een mooie symmetrische uitgangspuls.
Het zal nu duidelijk zijn dat de gemiddelde stromen die naar de uitgangen stromen heel nauwkeurig aan elkaar gelijk zijn. De linker stroom bestaan immers voor 50 % uit de stroom die door de linker weerstand wordt geleverd en voor 50 % uit de stroom die door de rechter weerstand wordt geleverd. Voor de rechter uitgang geldt precies hetzelfde.
Het volstaat de twee stromen door middel van condensatoren te middelen om twee gelijkstromen te verkrijgen die heel nauwkeurig aan elkaar gelijk zijn. Het probleem is verlegd naar het openen en sluiten van elektronische schakelaars met een duty-cycle van precies 50 %. Een digitaal probleem dat zonder moeilijkheden is op te lossen als de schakelfrequentie niet te hoog is.
 |
| Het principe van het 'Dynamic Element Matching' systeem. (© 2020 Jos Verstraten) |
Meerdere bits
Met één DEM-schakeling kan men een stroom 2.I omzetten in twee stromen 1.I. Door diverse identieke schakelingen te cascaderen volgens het rechter schema kan men uit de ene basis stroombron 2.I stromen genereren van 1.I, ½.I, ¼.I, etc.
Praktische schakelingen
In de praktische DEM-schakelingen wordt het principe verder uitgewerkt. Een stroom 4.l wordt nu door een ingewikkelder schakelaarsysteem omgezet in drie stromen van respectievelijk 1.I, 1.I en 2.I.
Een van de stromen 1.I wordt dan weer gebruikt als basis voor het volgende element uit de gecascadeerde keten, zodat stromen van ¼.I, ¼.I en ½.I ontstaan.
De DAC met geïntegreerde variabele pulssturing
Principe van het systeem
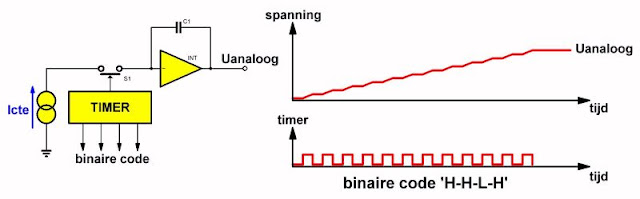
Andere fabrikanten hebben een ander alternatief ontwikkeld voor het stroom gestuurde R-2R systeem. Er wordt, net zoals bij het vorige systeem, uitgegaan van slechts één stroombron. Het basisprincipe van het systeem, voor de eenvoud toegepast op een vier bit systeem, is getekend links in de onderstaande figuur. De stroombron Icte is via een elektronische schakelaar S1 aangesloten op een integrator. Als een integrator gestuurd wordt met een constante stroom, dan zal de uitgangsspanning van de schakeling een lineair stijgende spanning zijn waarvan de stijgtijd evenredig is met de grootte van de constante stroom.
De binaire code op de ingangen wordt door een timer omgezet in een eenmalige pulstrein. Het aantal pulsjes in deze trein is gelijk aan het binaire gewicht van de digitale code. Als de code 'L-L-L-L' is levert de timer géén pulsjes. Is de code gelijk aan 'L-L-L-H' dan zal de timer één smal pulsje leveren dat de schakelaar S1 even sluit. Is de code gelijk aan 'H-H-L-H' dan levert de timer, zie rechts in de bovenstaande figuur, een pulstrein die is samengesteld uit 12 pulsjes.
De uitgangsspanning Uanaloog zal nu recht evenredig zijn met het aantal pulsjes in de pulstrein, daar zorgt de integrator wel voor. Zorgen 15 pulsjes voor een uitgangsspanning van 150 mV dan zal een pulstrein met slechts 7 pulsjes een analoge uitgangsspanning van 70 mV tot gevolg hebben. Het analoge probleem van de nauwkeurigheid van de stroombron(nen) wordt ook nu handig omzeild en verlegd naar een digitaal probleem, namelijk zet de binaire code op de ingangen om in een pulstrein. Een probleem dat zonder enige onnauwkeurigheid opgelost kan worden!
 |
| De DAC met geïntegreerde variabele pulssturing. (© 2020 Jos Verstraten) |
Sample-and-hold noodzakelijk
Op de uitgang verschijnt gedurende de digitaal naar analoog omzetting een trapvormig verlopende spanning. Alleen de eindwaarde van deze spanning is echter van belang. Het zal duidelijk zijn dat het noodzakelijk is deze eindwaarde na het omzettingsproces te bewaren in een sample-and-hold schakeling (S&H). Nadat de volgende conversie is voltooid is volstaat het de nieuwe topwaarde van de trapvormige spanning weer in de S&H in te lezen.
Over sample-and-hold schakelingen is op dit blog een eigen artikel geschreven, lees: Componenten: sample and hold.
Voor- en nadelen van het systeem
Enig bezwaar van de schakeling is dat de frequentie van de pulsjes uit de pulstrein gelijk moet zijn aan het aantal codecombinaties dat de digitale ingangscode kan bevatten, vermenigvuldigd met het aantal codecombinaties dat per seconde aan de DAC wordt aangelegd.
Voordeel is echter dat de schakeling absoluut geen last heeft van glitches (lees verder), dit vanwege de integrator en de noodzakelijke sample and hold.
Deglitching technieken
Inleiding
Een verhaal over digitaal naar analoog omzetting kan niet geschreven worden zonder aandacht te besteden aan het verschijnsel 'glitching'. Een fundamenteel probleem bij alle schakelaar gestuurde digitaal naar analoog omzetters is dat er gedurende de overgang van de ene naar de volgende ingangscode op de analoge uitgang van de schakeling korte, onvoorspelbare stoorpulsen ontstaan. Deze pulsen worden 'glitches' genoemd en deze storingen moeten in de meeste gevallen uit het analoge signaal worden verwijderd.

Het ontstaan van glitches
Glitches ontstaan doordat niet alle elektronische stroomschakelaars in de DAC even snel van de ene naar de andere toestand schakelen. Bij het aanpassen van de analoge uitgangsspanning aan een nieuwe digitale code op de ingangen zal in het gunstigste geval slechts één schakelaar van stand verwisselen. Het kan echter ook zijn dat alle schakelaars moeten omschakelen.
Het gevolg is dat de glitches niet allemaal even groot en breed zijn. Een onregelmatig stoorsignaal heeft een zeer brede bandbreedte en is dus rijk aan harmonischen. Bij audio-toepassingen zullen de glitches zorgen voor een typisch ruisgeluid dat met de bekende filtertechnieken nauwelijks is te onderdrukken.
In de onderstaande figuur is de situatie geschetst die bij een acht bit brede DAC ontstaat als de ingangscode omschakelt van 'L-H-H-H-H-H-H-H' naar 'H-L-L-L-L-L-L-L'. Op dat moment doet zich, althans wat glitches betreft, de slechtst mogelijke situatie voor omdat alle stroombron schakelaars in de DAC moeten omschakelen. Nu werken deze schakelaars niet even snel. Het kan dus gebeuren dat eerst de schakelaar van het MSB omschakelt, waardoor het lijkt alsof de digitale code even gelijk wordt aan 'H-H-H-H-H-H-H-H'. De analoge uitgang zal naar de hoge spanning willen schakelen die overeen komt met deze code. De uitgangsspanning van de DAC gaat dus plotseling stijgen. Alvorens echter de eindwaarde van deze foutieve code is bereikt zullen ook de andere stroombron schakelaars omgeschakeld zijn. De analoge uitgang gaat dan terug dalen naar de waarde die overeen komt met de nieuwe ingangscode. Op de uitgang ontstaat dus een zeer smalle positieve piek, een positieve glitch.
Als echter de MSB-schakelaar als laatste omschakelt ontstaat even een situatie waarbij het lijkt alsof de ingangscode gelijk is aan 'L-L-L-L-L-L-L-L'. Op dezelfde manier kunt u aantonen dat er nu een negatieve glitch ontstaat.
Het tijdsinterval waarin deze verschijnselen zich afspelen wordt de 'skew tijd' genoemd.
 |
| Het ontstaan van glitches. (© 2020 Jos Verstraten) |
HF-filteren
Glitches zijn zeer smalle pulsen en dus per definitie zeer hoogfrequent. Door achter de DAC een scherp afsnijdend laagdoorlaat filter op te nemen zal de bandbreedte van het uitgangssignaal beperkt worden, waardoor de hoogfrequente componenten waaruit de glitches bestaan worden verzwakt. Zeer scherp afsnijdende filters hebben echter een aantal nadelen. Op de eerste plaats veroorzaken zijn vertragingen hetgeen bij snel werkende DAC's ontoelaatbaar is. Op de tweede plaats veroorzaken zij faseverschuivingen waardoor vervormingen op het analoge uitgangssignaal kunnen ontstaan. Op de derde plaats hebben zij een zeer slechte respons op pulsen, waardoor overshoots op de uitgang ontstaan.
Analoge laagdoorlaat filters zijn dan ook alleen toepasbaar als er aan de schakelingen niet al te hoge eisen worden gesteld.
Speciale deglitcher schakelingen
Het principe van deze schakelingen is getekend in de onderstaande figuur. Het analoge uitgangssignaal van de DAC wordt aan een zeer snelle sample-and-hold aangeboden. Deze slaat het uitgangssignaal van de DAC op in een kleine condensator. De sample-schakelaar wordt geopend op het moment dat een nieuwe digitale code in de DAC wordt ingelezen. De glitches, die op dat moment op de uitgang van de DAC ontstaan, worden dus niet doorgegeven naar de condensator. Nadat de skew tijd verstreken is wordt de schakelaar gesloten, de condensator wordt snel opgeladen tot de nieuwe waarde van de analoge uitgangsspanning.
 |
Het principe van een deglitcher. (© 2020 Jos Verstraten) |
Op deze manier zou men in theorie helemaal geen last mogen hebben van de glitches. De goede werking van de schakeling is echter volledig afhankelijk van de timing tussen de puls die de nieuwe digitale gegevens in de DAC inleest en de puls die de elektronische schakelaar in de deglitcher bestuurt. Als dit stuursignaal te laat arriveert, bijvoorbeeld door systeemvertragingen, dan zal de schakelaar te laat openen en zal toch nog een deel van de glitches tot de condensator doordringen.
Bovendien heeft een S&H in de HOLD-stand een bepaalde doorkoppeling van de ingang naar de uitgang. De capaciteit van de schakelaar zal een deel van de hoogfrequente glitchpulsen toch naar de hold-condensator doorkoppelen.
Bestel uw behuizingen bij Amazon
