Het oppervlak van de compact disk
Van analoge audio naar 2 x 16 bit
Zoals u ongetwijfeld weet worden de twee analoge audiosignalen links en rechts digitaal op een audio-CD geperst. Er worden van beide signalen iedere seconde 44.100 samples genomen. Deze samples worden omgezet in 16 bit brede digitale woorden volgens een proces dat 'lineaire PCM' heet. Ieder sample wordt op dezelfde manier gedigitaliseerd. Zelfs als een sample niets anders dan wat achtergrondruis bevat wordt het tóch omgezet in een 16 bit breed digitaal woord. Dat de meeste bits van zo'n woord 'L' zijn wordt voor lief genomen, bij het ontwikkelen van het audio-CD systeem was men nog niet zo ver dat er op een intelligente manier gedigitaliseerd kon worden.
1.411.200 audio-bits per seconde
Dat betekent dus dat er per seconde speelduur niet minder dan 1.411.200 audio-bits in het oppervlak van de audio-CD worden geperst. Reken maar na! Twee keer digitaliseren met 16 bits levert 32 bits op per sample. Als dat 44.100 keer per seconde gebeurt levert dat inderdaad een datastroom van 1.411.200 bits per seconde op.
Natuurlijk staan er nog meer gegevens op de audio-CD, zoals de namen van de muzieknummers, uitvoerenden, lengte van de nummers, gegevens over de plaats van de nummers op de spiraal, foutcorrecties, etc.
De informatiedrager van de audio-CD
De audio compact disk bestaat uit een ongeveer 1,2 mm dikke plaat uit acrylplastic met een diameter van 12 cm. De audio-informatie is aan de bovenzijde van deze plaat aanwezig onder de vorm van een groot aantal zogenaamde nokken en dammen. De nokken (pits) zijn microscopisch kleine putjes die in het oppervlak van de plaat worden geperst. De dammen (lands) vormen het onaangetaste plaatoppervlak tussen de nokken. De overgangen tussen de nokken en de dammen noemt men de tikken. Iedere nok heeft dus twee tikken, een bij het begin van de nok en een bij het einde van de nok. Niet de nokken of de dammen, maar de tikken vormen de belangrijkste informatiebron van de audio-CD.
De nokken zijn uiteraard niet willekeurig op het oppervlak aangebracht, maar volgens een spiraalvormig spoor. Deze spiraal heeft gemiddeld 20.000 windingen hetgeen overeen komt met ongeveer 600 windingen per millimeter. De windingen van de spiraal hebben een onderlinge afstand van 1,6 μm. De nokken hebben een diepte van 0,12 μm, een breedte van 0,6 μm en een lengte van 0,8 μm tot 3,5 μm.
Voor de duidelijkheid: één micrometer is éénduizendste van een millimeter.
Nadien wordt er een aluminium laag opgedampt, zodat het oppervlak van de audio-CD reflecterend wordt.
 |
| Het oppervlak van een audio-CD onder de elektronenmicroscoop. (© 2007 Wikimedia Commons) |
De nokken worden bij de fabricage van de plaat onder grote druk in het half vloeibare dragermateriaal geperst. Om zoveel mogelijk informatie op één plaatje te persen moeten de nokken zo klein mogelijk zijn. Er worden echter technologische en systematische beperkingen gesteld aan de minimale afmetingen van de nokjes. De voornaamste systematische beperking is de zogenaamde numerieke apertuur van het optische systeem dat met een laserstraal de audio-CD aftast. Deze grootheid is gelijk aan het product van de openingshoek van de lichtstraal en de brekingsindex van de tussenstof.
Uit de optische theorie kan men berekenen dat voor het gegeven systeem een numerieke apertuur van 0,5 haalbaar is. Dat wil zeggen dat de afmeting van de lichtvlek in het brandpunt gelijk is aan 1 μm. Om deze kleine lichtvlek nog goed te kunnen detecteren mogen de nokken niet smaller zijn dan ongeveer 0,5 μm en moet de minimale lengte gelijk zijn aan 0,8 μm. De positie van de nokken en de dammen op het plaatoppervlak is nog eens overzichtelijk samengevat in de onderstaande figuur.
 |
| De afmetingen van de datadragers op de audio-CD. (© 2020 Jos Verstraten) |
Het uitlezen van de spiraal
Door technologische beperkingen hebben de nokken geen scherpe randen maar zijn enigszins afgerond. Dat heeft vervelende consequenties voor het signaal dat wordt uitgelezen en is de oorzaak van een van de vele noodzakelijke code-omzettingen. De spiraal wordt beschenen door rood laserlicht. Zoals u weet is het oppervlak van de schijf spiegelend. Het rode licht reflecteert op dit oppervlak. De mate van reflectie is echter afhankelijk van het gegeven dat de straal op een nok, een dam of een tik kan vallen. De gereflecteerde straal wordt in de optische pick-up opgevangen door een aantal gevoelige fotodiodes. Op deze manier wordt de informatie die op de audio-CD is geperst omgezet in een elektrische signaal.
Dit signaal bestaat dus uit een seriële datastroom. In principe zou deze stroom moeten bestaan uit mooie scherpe pulsen. Door de afgeronde en gerafelde kanten van de nokken is dat niet het geval. Het elektrische signaal heeft zelfs een tamelijk grote stijgtijd. De vorm van het uitgelezen signaal is weergegeven in de onderstaande figuur. Het signaal is enigszins driehoekvormig en bovendien niet constant in grootte. De grote stijg- en daaltijden worden bepaald door de onscherpe overgang tussen nok en dam. Dat de grootte van de puls afhankelijk is van de lengte van de nok heeft te maken met de fysische en elektronische beperkingen van de fotodetectoren in de pick-up. In ieder geval blijkt dat het uitgelezen signaal geen mooie digitale blokgolf is, maar eerder een analoog signaal. Er moet dus een soort schmitt-trigger tussen geschakeld worden. Zoals later zal blijken kan deze schakeling alleen goed werken als er iets speciaals wordt gedaan met de codering van het signaal.
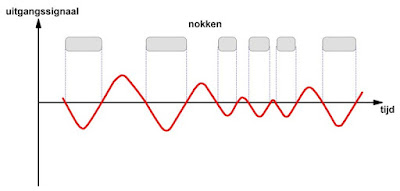 |
| Het elektrisch signaal dat de optische pick-up levert. (© 2020 Jos Verstraten) |
Het gegevensformaat op de audio-CD
De tikken staan voor logisch 'H'
Een van de grootste misverstanden die er bij de interpretatie van het audio-CD systeem wordt gemaakt is dat men denkt dat de nokken en de dammen corresponderen met 'L' en 'H' uit de digitale code. Niets is echter minder waar! Zoals uit de onderstaande figuur blijkt staan zowel de nokken als de dammen op de plaat voor logisch 'L'. Alleen de niveau-overgangen, dus de tikken, staan voor logisch 'H'. Dat heeft de nogal absurde consequentie dat er nooit twee opeenvolgende logische 'H'-signalen in de datastroom kunnen voorkomen. Wij komen daar later op terug.
 |
| Het verband tussen de seriële datastroom en de nokken en dammen op de plaat. (© 2020 Jos Verstraten) |
De twee analoge audiosignalen worden bij het audio-CD systeem bemonsterd met een snelheid van 44,1 kHz en omgezet in twee 16 bit lange digitale monsters. Alvorens deze audiocodes echter op de CD worden gezet, ondergaan de monsters een heleboel bewerkingen en worden aangevuld met een heleboel extra gegevens. Dat zijn:
- Een SYNC-code, die in de CD-speler gebruikt wordt voor het herwinnen van de klokfrequentie waarmee de bits op de CD zijn geschreven.
- De zogenaamde C&D-code, waarin extra informatie wordt ondergebracht, onder andere over de speelduur en het volgnummer van het muziekstuk dat gespeeld wordt.
- Acht in twee groepen van vier samengevoegde pariteit-codes, waarmee de elektronica van de CD-speler in staat is te onderzoeken of een uitgelezen code foutloos is ontvangen. Is dat niet het geval dan kan de elektronica aan de hand van de gegevens in deze codes de foutieve code herstellen, zodat het geluid niet wordt vervormd.
- Een packing-code, die noodzakelijk is voor het optimaal omzetten van het analoge uitgangssignaal van de pick-up in een digitale puls.
Al deze digitale gegevens worden in een specifiek patroon in de spiraal van de audio compact disk aangebracht. Eén zo'n patroon noemt men een raster of frame en de samenstelling is getekend in de onderstaande figuur.
Per frame worden er zes monsters van beide audiokanalen verwerkt. Omdat er, zoals reeds bekend, bemonsterd wordt met een frequentie van 44,1 kHz moeten er dus 44.100 gedeeld door 6 is gelijk aan 7.350 rasters per seconde op de plaat worden gezet.
Ieder vierkantje in de tekening stelt één CD-byte voor. De 2 x 6 audiomonsters worden ondergebracht in 2 x 12 CD-bytes om de heel eenvoudige reden dat het te complex zou zijn om de 16 bit lange woorden van het gedigitaliseerde geluid in één keer te verwerken. In totaal bevat een frame dus:
- 1 x SYNC-byte
- 1 x C&D-byte
- 12 x AUDIO-bytes
- 4 x PARITY-bytes
- 12 x AUDIO-bytes
- 4 x PARITY-bytes
De genoemde packing-code zit verweven in de bytes en is niet afzonderlijk in de samenstelling van het frame terug te vinden.
Het CD-byte
Om redenen die later worden toegelicht bestaat een fundamenteel CD-byte niet uit 8 bit, zoals gebruikelijk in de digitale techniek, maar uit niet minder dan 17 bits. Daarvan dragen 14 bits de eigenlijke informatie en worden drie extra bits toegevoegd (de packing-code) om redenen die later aan de orde komen.
 |
| De samenstelling van één frame op de audio-CD. (© 2020 Jos Verstraten) |
In de volgende paragrafen zal uitvoerig worden ingegaan op het nut, de noodzaak, de samenstelling en de consequenties van alle genoemde extra coderingen.
De digitalisatie van het audiosignaal
Inleiding
Allereerst moet men uiteraard de twee analoge audiosignalen digitaliseren. Dit proces omvat:
- Het bemonsteren van de analoge signalen tot 16 bit brede woorden.
- Het splitsen van de twee 16 bit lange bemonsteringscodes in 4 x 8 bit brede bytes.
- Het verzamelen van de gegevens van zes opeenvolgende monsters.
- Het groeperen van de even en oneven bytes uit deze monsters.
- Het aan elkaar rijgen van al deze gegevens tot een seriële code.
Het signaal wordt 44.100 keer per seconde bemonsterd met een resolutie van 16 bit, zodat er in totaal 2 · 44.100 · 16 = 1.411.200 bit per seconde verwerkt moeten worden.
Samenstelling van de code
De twee 16 bit woorden per monster worden gesplitst in een LSB en een MSB, die beide uit 8 bit bestaan. Deze vier bytes vormen de digitale representatie van één bemonstering en de 32 bit worden één audiosymbool genoemd. De audiosymbolen van zes opeenvolgend bemonsteringen worden tot slot samengevoegd tot één raster. Dit raster bestaat dus uit 32 audiosymbolen van ieder 8 bit.
De hoogst noodzakelijke foutcorrectie
Inleiding
Het is uitgesloten dat er ook maar één audio-CD wordt geperst, waarop niet duizenden van de miljarden aanwezige nokjes beschadigd zijn. Het is voldoende dat er tijdens het opdampen van de aluminium reflecterende laag een uiterst klein stofdeeltje op het oppervlak terecht komt om tientallen nokjes niet reflecterend te maken en dus niet uitleesbaar.
Grote audio vervorming
Ieder fout uitgelezen bit vervormt de uiteindelijk herwonnen analoge audiomonsters. Als zo'n beschadigde code door de DAC in de CD-speler in een analoog signaal wordt omgezet kan dit tot gevolg hebben dat er zeer korte maar zeer steile pieken in het analoge uitgangssignaal ontstaan. Iedere foutief uitgelezen code genereert dus een tik in de weergave. Zonder uitgebreide foutcorrectie systemen zou een audio-CD waarschijnlijk nog harder spetteren en tikken dan zelfs de slechtste analoge vinyl plaat!

Digitale foutcorrectie
Bij digitale geluidsverwerking is het gelukkig geen enkel probleem zo veel foutcorrectie systemen in te bouwen als men wil. Er moet uiteraard wel een compromis gevonden worden tussen de kans dat er toch nog foutieve codes in de DAC terecht komen en de extra elektronica die noodzakelijk is in de weergave apparatuur.
Bij het audio-CD systeem heeft men gekozen voor twee correctietechnieken:
- Het invoegen van parity-bits:
Deze bits worden berekend aan de hand van de samenstelling van de audio-bytes. Er wordt gekeken hoeveel bits in een matrix 'L' of 'H' zijn. Door middel van de parity-bits wordt dit aantal even of oneven gemaakt. - CIRC-codering van de digitale datastroom:
CIRC staat voor 'Cross Interleaved Reed-Solomon Code'. In deze stap worden opeenvolgende bytes van de datastroom op een zeer ingewikkelde manier door elkaar gehusseld. De bedoeling hiervan is dat fouten in het medium, die opeenvolgende bytes aantasten, geen enkele fundamentele code zo zwaar beschadigen dat deze niet meer hersteld kan worden.
Invoegen van de pariteit-bits Q
Inleiding
Het zal duidelijk zijn dat een enkele foutcorrectie met pariteit-bits niet voor 100 % betrouwbaar is. Er zouden immers twee of meerdere bits foutief kunnen zijn uitgelezen, waardoor de controle van het even aantal 'H'-bits toch klopt. Vandaar dat er twee pariteit-controles worden uitgevoerd. Er worden twee soorten parity-bits in de digitale data-stroom ingevoegd:
- de Q-parity
- de P-parity
De Q-bits worden voor de CIRC-codering aangebracht, de P-bits nadien.
Matrixcodering en toevoegen bits
De Q-parity is de eerste stap in het ingewikkelde systeem van de totale foutcorrectie. De systematiek in het samenstellen van deze bytes is vrij eenvoudig en wordt vereenvoudigd uitgelegd aan de hand van de onderstaande figuur. De digitale audio-codes worden omgezet in een matrix die bestaat uit een aantal horizontale en een aantal verticale lijnen. Op ieder snijpunt van een horizontale met een verticale lijn wordt een bit geplaatst.
In de illustratie is dat op vereenvoudigde schaal voorgesteld door de bits X1 tot en met X12, die zijn opgenomen in een matrix met drie horizontale en vier verticale lijnen. Aan iedere rij en aan iedere kolom wordt nu een Q pariteit-bit toegevoegd (Q1 tot en met Q3 en Q5 tot en met Q8) dat ervoor zorgt dat het aantal 'H'-bits in iedere rij en in iedere kolom even is. Als bijvoorbeeld in de bovenste rij X1 tot en met X4 maar één bit 'H' is, dan zal het pariteit-bit Q1 ook 'H' worden om het aantal hoge bits in deze rij even te maken. Tot slot wordt de matrix aangevuld met het pariteit-bit Q4 dat ervoor zorgt dat het aantal hoge bits ook in het pariteit-byte even is.
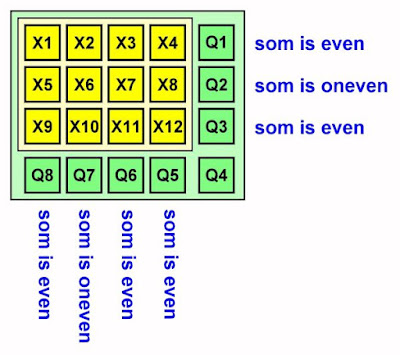 |
| De samenstelling van het Q pariteit-byte. (© 2020 Jos Verstraten) |
In de CD-speler zijn schakelingen aanwezig die in eerste instantie nagaan of het aantal hoge bits in de pariteit-bytes even is. Is dat niet het geval, dan zit er een fout in het pariteit-byte zélf en kan de foutcorrectie niet worden toegepast. Is het aantal hoge bits wel even, dan is het pariteit-byte betrouwbaar en kan de decodering de matrix samenstellen en controleren of er in iedere rij en in iedere kolom een even aantal hoge bits is ontvangen. Is dat het geval, dan wordt het byte goed verklaard. Is dat echter niet het geval, dan kan de logica op een vrij eenvoudige manier vaststellen welk bit verkeerd is uitgelezen. Stel bijvoorbeeld, zoals getekend in de bovenstaande figuur, dat in de tweede rij en in de tweede kolom een oneven aantal 'H'-bits wordt vastgesteld. De elektronica weet dan met stelligheid te melden dat bit X6 foutief is uitgelezen. Dit bit kan hersteld worden en de fout is gecorrigeerd.
De CIRC-codering
Inleiding
Het systeem met de parity-bytes werkt prima zolang er maar enkele bits uit een byte verkeerd overkomen. De ruimte die de bits op de spiraal innemen is echter zo klein dat het in de praktijk zelden zal voorkomen dat slechts enkele bits beschadigd zijn. Bij een beschadiging van de audio-CD worden volledige bytes of zelfs volledige audio-samples foutief uitgelezen en tegen dergelijke codebeschadigingen is het parity-systeem niet opgewassen.
Reed en Solomon
Twee statistici, verbonden aan de researchafdeling van Sony, bedachten reeds in 1960 een oplossing voor dit probleem. Deze oplossing werd door Sony en Philips geselecteerd als het voornaamste foutcorrectie algoritme voor het audio-CD systeem. De kans dat een volledig zestien bit breed audiomonster foutief wordt uitgelezen wordt minder groot als de informatie in deze bytes over een langere lengte van de spiraal wordt verspreid. Als dat niet kan door de individuele bits langer te maken, dan moet het maar gebeuren door de digitale informatie van verschillende opeenvolgende monsters door elkaar te husselen waardoor de informatie van één audio-monster over een grote afstand op de spiraal wordt geschreven.
CIRC: Cross Interleaved Reed–Solomon Coding
De twee genoemde wiskundigen hebben een procédé ontwikkeld waarbij een zo gunstig mogelijk compromis wordt bereikt tussen enerzijds de noodzakelijke decodeerelektronica in de CD-speler en anderzijds een maximale kans op herstel van fouten in de code. Het systeem heet 'CIRC' en hoe dit aan de codeerzijde, dus in de studio, wordt toegepast is schematisch voorgesteld in de onderstaande figuur.
De audio-bytes en de Q parity-bytes worden door vertragingsschakelingen gestuurd. Deze zijn schematisch voorgesteld door de grote driehoek. Ieder byte krijgt een andere vertragingstijd. Bij digitale systemen is dit geen enkel probleem. Het volstaat immers alle bytes aan seriële schuifregisters aan te bieden, die ieder uit een bepaald aantal cellen bestaan. Alle registers worden met de systeemklok gestuurd. Als een register uit 8 cellen bestaat zal het byte dat aan de ingang wordt aangelegd 8 klokperioden later op de uitgang verschijnen. Er ontstaat dus een vertraging over 8 perioden. Het gevolg is dat op de uitgangen van de schuifregister weliswaar audio-monsters en Q parity-bytes worden terug gevonden, maar dat deze niet allemaal afkomstig zijn van hetzelfde frame. Terwijl de bovenste audio-monsters de vertragingslijn alweer hebben verlaten, zitten de onderste monsters nog ergens in hun schuifregisters. Op de uitgangen van deze lange registers staan de audio-bytes van de vorige monsters.
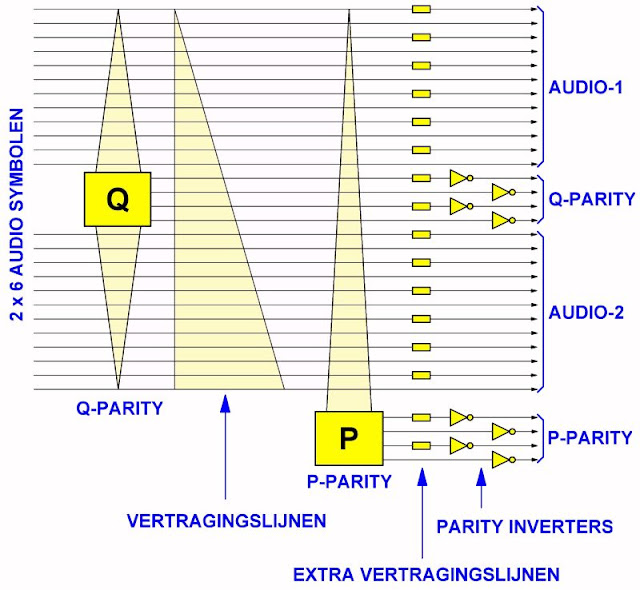 |
| Het CIRC-procédé symbolisch voorgesteld. (© 2020 Jos Verstraten) |
Invoegen van de parity-bits P
Op de door elkaar gehusselde bytes wordt in een volgende fase een tweede pariteit-controle P toegepast. De vier berekende P parity-bits worden achter de laatste serie audiogegevens opgenomen.
De resultaten van de foutcorrectie
Twee soorten leesfouten
Bij het uitlezen van een audio-CD kunnen er twee soorten fouten ontstaan:
- korte fouten
- lange fouten.
Korte leesfouten
De even/oneven vertraging van de bytes, waardoor de gegevens van door elkaar gehusselde monsters in twee opeenvolgende datablokken worden opgenomen is ideaal voor het corrigeren van kleine foutjes in het bitbereik. De decoder in de CD-speler kan aan de hand van de gegevens in de P parity-bytes de foutieve bits snel herkennen en herstellen.
Lange leesfouten
Grotere beschadigingen op het oppervlak van de audio-CD hebben tot gevolg dat meerdere datablokken volstrekt onbruikbaar worden. Er wordt dan gebruik gemaakt van het feit dat de gegevens van één oorspronkelijk monster door elkaar gehusseld verspreid zijn over een groot aantal opeenvolgend datablokken. De decoder in de CD-speler zal dus altijd wel wat gegevens van twee opeenvolgende audiomonsters onbeschadigd terug vinden in die vele datablokken. Uit deze informatie en met behulp van de Q parity-bytes wordt in eerste instantie gepoogd zoveel mogelijk bytes te herstellen. Lukt dat niet, dan wordt een interpolatietechniek ingeschakeld waarbij de ontbrekende gegevens worden berekend door het gemiddelde te nemen van het vorige en volgende monster.
Herstelcapaciteit van het CIRC-procédé
Met het CIRC-procédé is het mogelijk aan de hand van de pariteit-controle fouten tot 4.000 bit te herstellen. Door het inschakelen van de interpolatietechniek is het zelfs mogelijk te corrigeren over 12.000 bit. Bij een audio-CD komt dat overeen met ongeveer 7,5 mm spoorlengte!
Het C&D-byte
Inleiding
'C&D' is de afkorting van 'Control and Display'. Dit ene byte per frame bevat een heleboel informatie over de inhoud van de CD, tijdcoderingen en zelfs alfanumerieke gegevens die op het scherm van een CD-speler met display weergegeven kunnen worden. Al deze gegevens kunnen gemakkelijk in dat ene byte per frame geschreven worden. Vergeet niet dat er 7.350 frames per seconde worden geschreven zodat er ook 7.350 C&D-bytes per seconde worden uitgelezen. De afzonderlijke C&D-bytes staan niet op zichzelf, maar worden verzameld in zogenaamde subcode datablokken. Ieder datablok bestaat uit 98 C&D-bytes, verzameld uit 98 opeenvolgende frames. In totaal worden er dus 7.350 gedeeld door 98 is gelijk aan 75 datablokken per seconde uitgelezen.
De samenstelling van de datablokken
De samenstelling van de datablokken is getekend in de onderstaande figuur. De bytes worden ingelezen in een matrix, opgebouwd uit 8 kolommen en 98 rijen. De twee eerste rijen, dus de twee eerste bytes van het blok, bevatten de synchronisatiepulsen S0 en S1. Deze hebben een unieke samenstelling, zodat de elektronica in de CD-speler deze bytes gemakkelijk kan identificeren.
De overige gegevens worden per rij uitgelezen. Een datablok bevat acht woorden, die ieder uit 96 bit bestaan. De woorden worden gekenmerkt door lettercodes P, Q, R, S, T, U, V en W. Van deze woorden zijn de P- en de Q-woorden het belangrijkst.
 |
| De samenstelling van een subcode datablok uit 98 C&D-bytes. (© 2020 Jos Verstraten) |
Het P-woord bevat gegevens waaruit de CD-speler kan afleiden dat er een nieuw muzieknummer wordt gestart of dat er een nieuwe passage uit een klassiek stuk aan de beurt komt. Deze zogenaamde 'startflag' bestaat uit het gedurende twee seconden opnemen van P-woorden die volledig gevuld zijn met 'H'. De microprocessor in de CD-speler kan zeer snel van de ene naar de andere startflag overschakelen. Dank zij de lange duur van deze flag moeten niet alle windingen van de informatiespiraal afgetast worden. De optische pick-up kan dus snel heen en weer over het oppervlak worden bewogen omdat de startflag vele windingen lang is.
Een tweede functie van het P-woord is het informeren van de elektronica dat de plaat is afgelopen. In de laatste windingen van de spiraal wordt het P-woord met een frequentie van 2 Hz gemoduleerd met enen en nullen. De microprocessor in de speler herkent deze code en treft de noodzakelijke maatregelen om het aftasten van de plaat te beëindigen, om de CD opnieuw af te spelen als de 'REPLAY'-functie is gekozen of om in CD-wisselaars de volgende audio-CD op de draaitafel te leggen.
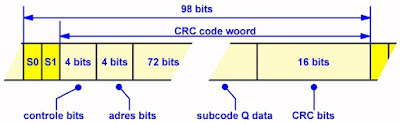 |
| De samenstelling van het Q-woord. (© 2020 Jos Verstraten) |
De samenstelling van dit woord is getekend in de bovenstaande figuur. De eerste twee bits maken deel uit van de synchronisatie S0 en S1 en hebben geen betekenis voor de samenstelling van het woord. Nadien volgen vier groepen bits, die de volgende betekenis hebben:
- Control bits:
Deze vier bits geven informatie over de samenstelling van de compact disk. De betekenis van alle bits is gegeven in de tabel van de onderstaande figuur. Hieruit blijkt dat men rekening heeft gehouden met het op de markt komen van vierkanaals systemen, dat de mogelijkheid bestaat copieerbeveiligingen in een CD-speler in te bouwen en dat zelfs rekening is gehouden met de uit de vinyltechniek bekende emphasís filtertechnieken voor de verbetering van de weergave van hoge tonen. - Adress bits:
Volgens de codering die gegeven is in de tabel bepaalt de samenstelling van de vier adress bits de mode van het Q-woord. Deze mode geeft aan wat de inhoud van de Q data bits voorstelt.
 |
| De samenstelling van de control en adress bits. (© 2020 Jos Verstraten) |
De drie modes die in de adress bits gedefinieerd worden hebben de onderstaande betekenis:
- MODE 1:
In MODE 1 geven de 72 bit van de Q-data informatie over de starttijd, de lengte en het nummer van het muziekstuk dat wordt gespeeld. Dank zij deze gegevens kan de CD-speler heel erg snel een bepaald nummer selecteren. Bovendien wordt in de Q-data een timer bijgehouden die de totale speelduur van de audio-CD weergeeft. - MODE 2:
In MODE 2 geven de D-data het zogenaamde 'Disc Catalogue Number', een soort ISBN-code voor audio-CD's waaruit onmiddellijk alle gegevens zoals uitgiftedatum, producent en uitvoerenden kunnen worden afgeleid. Dit nummer kan in 52 bit worden ondergebracht, zodat er plaats genoeg is in het woord om de timer van MODE 1 te kopiëren. - MODE 3:
In MODE 3 bevatten de data in de D-data de zogenaamde 'International Standard Recording Code ISRC'. Deze code is samengesteld uit vijf alfanumerieke karakters en zeven numerieke karakters. De ISRC is een unieke en permanente identificatie van een bepaalde opname en kan als een digitale vingerafdruk in een uitgave van die opname worden gecodeerd. Dit maakt het mogelijk om opnamen automatisch te identificeren bijvoorbeeld met het oog op het beheren van royalty's (innen van auteursrechten). De ISRC is verbonden aan de opname zélf en niet aan de fysieke vorm daarvan. Eenzelfde opname die wordt uitgebracht op audio-CD en DVD-audio heeft één en dezelfde ISRC.
Eight to Fourteen Modulation
Inleiding
Zoals reeds opgemerkt levert de optische pick-up geen signaal af met een constante amplitude. De grootte van het signaal is afhankelijk van de lengte van de nokken. Dat heeft tot gevolg dat het onmogelijk is de digitale waarde (het 'L' of 'H' zijn) van het signaal al te leiden van de amplitude. Vandaar dat men heeft besloten de tikken, dus de overgangen tussen nokken en dammen en tussen dammen en nokken, de digitale waarde 'H' te geven en zowel de nokken als de dammen gelijk te stellen aan digitaal 'L'. Men moet dan alleen de overgangen in het signaal detecteren om de digitale code te herwinnen, hetgeen op een vrij eenvoudige manier met een comparator kan worden uitgevoerd.
Verhogen van de klokfrequentie
De geschetste toekenning van digitale 'H' aan de tikken heeft een bijkomend voordeel. Een tik is veel smaller dan een nok. Een digitale 'H' moet dus niet langer worden voorgesteld door een nok met een minimale lengte van 0,8 μm, maar kan veel korter zijn. Daar heeft men dankbaar gebruik van gemaakt en men heeft de klokfrequentie waarmee het signaal op de audio-CD wordt geschreven verhoogd tot 4,3218 MHz.
Zoals bekend levert de ADC per seconde 2 x 16 x 44.100 = 1.411.200 bits. De frequentie van de audio datastroom is dus gelijk aan 1,4112 MHz. De klokfrequentie kan bijgevolg een factor drie verhoogd worden, waaruit men zou kunnen besluiten dat er drie keer zoveel informatie op een compact disk past. Dat dit echter niet het geval is zal dadelijk blijken.
Acht bit code te klein
De 32 bytes uit een raster bestaan allemaal uit 8 bits. Alle 256 mogelijke codecombinaties kunnen voorkomen. Er zullen dus tal van bytes bestaan waar twee of meerdere opeenvolgende bits 'H' zijn. Als men echter besluit een 'H'-bit voor te stellen door een tik, dan kan men alleen maar gebruik maken van de hogere klokfrequentie als er geen twee hoge bits achter elkaar voorkomen. Zo'n twee opeenvolgende 'H'-bits moeten immers worden voorgesteld door twee tikken, dus door een dam-nok-dam overgang. Een bit komt dan toch weer overeen met een schrijflengte van 0,8 μm en het voordeel van de zeer kleine ruimte (een tik) die nodig is voor het schrijven van een 'H' en de daaruit volgende hogere maximale klokfrequentie gaat weer verloren.
Van acht naar veertien
Om dit probleem op te lossen heeft men een nieuwe code ingevoerd, waarin nooit twee 'H'-bits achter elkaar voorkomen. Bovendien mogen in deze code nooit minder dan twee 'L'-bits achter elkaar optreden en mogen er ook nooit meer dan tien 'L'-bits achter elkaar aanwezig zijn.
Twee 'H'-bits worden dus minstens gescheiden door twee 'L'-bits, zodat de sequentie 'H-L-L-H' voorgesteld kan worden door één nok met de minimale breedte van 0,8 μm. Deze code kan dus zonder bezwaar met 4,3218 MHz op de plaat geschreven worden.
De grens van maximaal tien 'L'-bits achter elkaar wordt bepaald door de synchronisatiegrens in de CD-speler. De 'H'-bits worden immers mede gebruikt voor het synchroniseren van de klokoscillator in de CD-speler met de klok op de audio-CD en als er te lang geen 'H' verschijnt zou deze schakeling uit synchronisatie kunnen komen.
Blijft de vraag uit hoeveel bits deze nieuwe code moet bestaan. Men heeft berekend dat uit de 16.384 codecombinaties die een veertien bit woord kan bevatten er 267 aan de gestelde drie eisen voldoen. Daar passen de 256 acht bit codes die in een byte kunnen voorkomen mooi in! De acht bits brede audio-bytes worden dus omgezet in bepaalde veertien bits lange CD-bytes. Voor deze omzetting is uiteraard een gestandaardiseerde codetabel ontworpen, zodat in alle studio's waar audio-informatie wordt omgezet in CD-codering met dezelfde code-omzetting wordt gewerkt.
Deze stap in de codering wordt 'Eight to Fourteen Modulation', meestal afgekort tot 'EFM', genoemd. In de onderstaande figuur is het verband getekend tussen een audio-byte, het CD-byte en het patroon van nokken en dammen dat in de audio-CD wordt geperst.
 |
| Het verband tussen een audio-byte, een CD-byte en de nokken en dammen in de spiraal. (© 2020 Jos Verstraten) |
Invoegen van packing-bits
Inleiding
Zoals reeds opgemerkt levert de optische pick-up geen mooi signaal af, maar een soort sinusvormige spanning waarvan de amplitude afhankelijk is van de lengte van de nokken. In de onderstaande figuur is het typische beeld getekend dat op het scherm van een oscilloscoop verschijnt als u de uitgangsspanning van de optische pick-up met triggering op 0 V meet.
 |
| Het uitgangssignaal van de optische pick-up op het scherm van een scoop. (© 2020 Jos Verstraten) |
Dat is voorgesteld in de bovenste grafiek van de onderstaande figuur. In dit voorbeeld worden twee CD-bytes uitgelezen die meer laag dan hoog zijn. Het gevolg is dat de gemiddelde gelijkspanningswaarde van het pick-up signaal tamelijk negatief wordt.
Dat offsetverschijnsel is zeer ongewenst. Er kunnen namelijk timingfouten ontstaan in de schakeling die de uitgangsspanning van de optische pick-up omzet in een mooi digitaal signaal. Omdat de voor- en de achterflanken van het signaal tamelijk vlak verlopen zal het moment waarop de comparator omschakelt in bepaalde mate afhankelijk worden van de gelijkspanningsinhoud van het signaal. Dat is absoluut ongewenst omdat daardoor de verhouding tussen 'L' en 'H' kan worden verstoord.

De packing-bits en DSV-compensatie
Om deze CD-offset, die een gevolg is van de 'Digital Sum Value' (DSV) van de digitale code, zo gering mogelijk te houden worden er drie extra bits aan ieder CD-byte gekoppeld. Deze bits noemt men de 'packing-bits'. Het principe noemt men de 'DSV-compensatie'. Zoals voorgesteld in de onderste grafiek van de bovenstaande figuur wordt de inhoud van deze bits zo berekend dat de gemiddelde DSV zo gering mogelijk is. Het gevolg is dat het analoge uitgangssignaal van de optische pick-up geen offset heeft en de gemiddelde waarde de nul zo veel mogelijk benadert. In het getekende voorbeeld zorgen deze drie extra bits ervoor dat de polariteit van het tweede raster inverteert. Dammen worden nokken, nokken worden dammen. Omdat dammen en nokken voor logische lage niveaus staan heeft dat geen gevolgen voor de samenstelling van de code.
Het gevolg van deze invertering is wel dat de gemiddelde waarde van het signaal, die eerst door het uitlezen van het eerste frame tamelijk negatief was geworden, zich nadien weer naar de nul begeeft.
De tweede functie van de packing-bits
Zoals bekend mogen er nooit twee hoge bits achter elkaar voorkomen in de datastroom. Nu zou het echter kunnen zijn dat een CD-byte eindigt op een 'H' en het volgende begint met een 'H'. In dat geval zullen de drie packing-bits de samenstelling 'L-L-L' of 'L-L-H' krijgen waardoor de twee hoge bits door minstens twee lage bits worden gescheiden. Het derde bit wordt dan gebruikt voor het minimaliseren van de DSV.
Het SYNC-byte
Twee functies
Het SYNC-byte dat de aanvang van een nieuw frame aangeeft heeft twee functies. Op de eerste plaats weet de microprocessor uit de detectie van het byte dat een nieuw frame start. Op deze manier is de schakeling in staat de subcode te scheiden van de audio-informatie en de na het subcode byte ontvangen gegevens te splitsen in 12 audio-bytes, 4 Q parity-bytes, weer 12 audio-bytes en tot slot 4 P parity-bytes. Al deze bytes worden dan op de juiste manier in de schakeling gestuurd die zorgt voor het decoderen van de code.
Op de tweede plaats wordt de SYNC-puls, de naam zegt het zelf, gebruikt voor het synchroniseren van de locale oscillator met de klok van de gegevens op de audio-CD. In feite bevat de CD alleen duidelijke informatie over de hoge bits in de code. Dat zijn de tikken. De lage bits zijn niet aanwezig en moeten door de schakeling in de CD-speler terug tussen de hoge bits worden ingevoegd. Om dit zonder fouten te kunnen doen moet de klokfrequentie waarmee de CD beschreven is zo nauwkeurig mogelijk worden gereconstrueerd.
De samenstelling van het SYNC-byte
Dit byte bestaat als enige byte uit 27 klokperioden. Het is dus onmiddellijk door de elektronica in de CD-speler te herkennen. Zoals uit de onderstaande figuur blijkt is de informatie 24 bits lang. Deze wordt uiteraard aangevuld met de drie DSV-bits. Omdat dit byte precies 27 klokperioden bevat kan de microprocessor in de CD-speler de juiste frequentie van de CD-klok berekenen en de locale oscillator door middel van een PLL-schakeling desgewenst corrigeren.
 |
| De samenstelling van het SYNC-byte. (© 2020 Jos Verstraten) |
Samenvatting
De 136 μs van een frame
Omdat de volledige samenstelling van de digitale code die op het oppervlak van een audio-CD wordt geschreven zo complex is, herhalen wij tot slot nog eens de belangrijkste gegevens.
Een totaal audio-CD frame bevat:
- 27 clock-perioden voor het SYNC-byte
- 17 clock-perioden voor het C&D-byte
- 204 clock-perioden voor de eerste 12 audio-bytes
- 68 clock-perioden voor de Q-parity
- 204 clock-perioden voor de tweede 12 audio-bytes
- 68 clock-perioden voor de P-parity
Een frame neemt dus 588 clockperioden in beslag. De CD-clock heeft een frequentie van 4,3218 MHz. Een periode heeft dus een duur van 0,231 ns. Uit deze gegevens kunt u af leiden dat één frame een tijdsduur van 136 μs heeft.
Waarmee bewezen wordt dat er inderdaad 7.350 frame's per seconde worden geschreven!
Grafische samenvatting
Tot slot van dit vrij ingewikkeld verhaal geeft de onderstaande figuur een gedetailleerde beschrijving van de samenstelling van één frame uit de spiraal van een audio-CD.
 |
| De gedetailleerde samenstelling van één frame. (© 2020 Jos Verstraten) |
Bestel elektronica boeken bij Amazon



