Eerst wat theoretische achtergrondinformatie
Algemeen blokschema
Een oscillator is volgens het blokschema van de onderstaande figuur samengesteld uit een versterker, een meekoppeling, een amplitudebegrenzing en een frequentiebepalend netwerk. De meekoppeling bestaat uit een terugkoppeling van de uitgang naar de ingang, waarbij een deel van de uitgangsspanning in fase met de ingangsspanning aan de ingang wordt aangeboden. Door deze terugkoppeling zal het signaal aan de ingang vergroten. Deze hogere ingangsspanning wordt weer versterkt door de versterker en een deel van het versterkte signaal wordt weer in fase aan de ingang aangeboden. Zonder de amplitudebegrenzing zou het signaal dat in fase naar de ingang wordt teruggekoppeld er voor zorgen dat de uitgangsspanning binnen de kortste keren zou vastlopen tegen de massa en de voedingsspanning. De begrenzer zorgt ervoor dat het signaal op de uitgang zich stabiliseert op een bepaalde maximale waarde, waardoor het vastlopen wordt voorkomen en op de uitgang een mooie sinus ontstaat.
 |
| Algemene voorstelling van een oscillator. (© 2020 Jos Verstraten) |
Wil een schakeling kunnen oscilleren, dan moet aan twee belangrijke voorwaarden voldaan worden:
- De amplitude voorwaarde
De oscillatie ontstaat en zal in stand blijven, dan en slechts dan als de rondgaande versterking minstens gelijk is aan 1. In formulevorm: K • A ≥ 1. K is de koppelfactor, A de versterking van de versterker. Als K kleiner is dan A-1, dan zal de schakeling na het aanzetten niet gaan oscilleren. Als u de schakeling door een externe impuls toch in oscillatie brengt zal het signaal op de uitgang langzaam maar zeker uitsterven. - De fase voorwaarde
Een deel van de uitgangsspanning moet in fase op de ingang van de schakeling verschijnen. Onder de vorm van een formule: φ = 0°.
Het is niet zo moeilijk aan de amplitude voorwaarde te voldoen. U zou immers de versterking erg hoog kunnen maken. Maar dit heeft als nadeel dat de schakeling zal vastlopen, hetgeen grote vervormingen met zich meebrengt. In feite moet dus na de start van de oscillatie de voorwaarde aangepast worden in K • A = 1.
Dit kan alleen maar door gebruik te maken van automatische versterkingsregelingen. U kunt immers nooit een versterking zo nauwkeurig afregelen dat onder alle voorwaarden aan de gestelde formule wordt voldaan.
De fase voorwaarde
U kunt aan de fase voorwaarde voldoen door een afgestemde kring in de terugkoppeling of in de uitgang van de versterker op te nemen. De frequentie waarop de schakeling zal oscilleren, is alleen afhankelijk van de eigenschappen van deze afgestemde kring. Voorwaarde is dat deze kring voor slechts één frequentie een faseverschuiving van 0° heeft. U kunt zowel RC- als LC-kringen toepassen. De eerste treft u voornamelijk aan in laagfrequente schakelingen, de tweede in hoogfrequente oscillatoren.
Seriële of parallelle voeding
De voedingsspanning van de oscillatorschakeling kan zowel in serie als parallel met de afgestemde kring worden aangeboden. Bij de serie-voeding zijn de transistor, de afgestemde kring en de voeding volgens het schema van de onderstaande figuur in serie geschakeld. Nadeel van deze methode is dat er een gelijkstroom door de spoel van de afgestemde kring vloeit en dat dit de magnetische eigenschappen van de kern van de spoel kan beïnvloeden. Zou door deze gelijkstroom de kern van de spoel in magnetische verzadiging gestuurd worden, dan zal de inductantie van de spoel wijzigen en daarmee natuurlijk ook de frequentie. De condensator C3 zorgt voor een effectieve wisselspanningsontkoppeling van de resonantiekring, waardoor de wisselstroomketen gesloten wordt.
 |
| Seriële voeding via de afgestemde kring. (© 2020 Jos Verstraten) |
 |
| Principe van de parallelle voeding van de trap. (© 2020 Jos Verstraten) |
Er beslaan ontelbare soorten oscillatoren, waarvan de meeste genoemd zijn naar de man (of vrouw) die de schakeling ontwerpen heeft. In dit artikel worden de onderstaande basisschakelingen besproken:
- De Meißner oscillator.
- De Colpitts oscillator.
- De Hartley oscillator.
- De capacitieve terugkoppeling oscillator.
- De Wien brug oscillator.
- De faseverschuiving oscillator.
- De kristal oscillator.
Transistoren of op-amp's?
U kunt laagfrequent oscillatoren zowel met transistoren als met op-amp's opbouwen. Als u echter hoger dan 1 MHz moet gaan kunt u het gebruik van op-amp's rustig vergeten en moet u het met transistoren doen. De meeste populaire op-amp's hebben immers maar een beperkte bandbreedte en laten het afweten in het MHz-bereik. Bovendien zijn bepaalde schakelingen in de praktijk uitsluitend geschikt voor het samenstellen van HF-oscillatoren. Voor lagere frequenties zou u onhandelbaar grote spoelen of zelfinducties moeten gebruiken.
De Meißner oscillator
De werking
Bij dit type oscillator wordt het teruggekoppelde signaal bij gebruik van een emitter-schakeling naar de basis terug geleid en bij gebruik van een basis-schakeling naar de emitter. In de onderstaande figuur is het principeschema van beide schakelingen weergegeven.
Met de potentiometer R2 kunt u het werkpunt van de transistor instellen, de waarde van de potentiometer R4 bepaalt de mate van terugkoppeling. De condensator C1 zorgt ervoor dat de gelijkspanning niet via L1 kortgesloten kan worden. De terugkoppelspoel L1 heeft, vanwege de zeer lage ingangsimpedantie van de transistor, slechts enige windingen. Bij de basis-schakeling wordt inductief teruggekoppeld naar de emitter. De condensator C4 legt de basis voor signaalspanningen aan de massa.
 |
| Principe van de Meißner oscillator, links met emitter-schakeling, rechts met basis-schakeling. (© 2020 Jos Verstraten) |
U kunt de demping van de kring door de collectorbelasting aanmerkelijk reduceren als u, zoals in de schema's getekend, de collector op een aftakking van de primaire spoel L2 aansluit. Bovendien wordt door deze aftakking de uitgangsimpedantie van de schakeling omhoog getransformeerd.
De Colpitts oscillator
De werking
Deze oscillatorschakeling werkt volgens het principe van de capacitieve driepunt schakeling. Zoals uit de onderstaande schema's blijkt is de resonantiekring samengesteld uit twee in serie geschakelde condensatoren C1 en C2 en één spoel L1. De terugkoppeling vindt plaats van de collector naar de basis bij de emitter-schakeling en van de collector naar de emitter in de basis-schakeling. Het derde element (respectievelijk de emitter en de basis) wordt door een condensator ontkoppeld naar de massa. Bij de emitter-schakeling is dat C4, bij de basisschakeling C3.

Opmerking
Bij de basis-schakeling zijn de in- en de uitgangskringen volledig van elkaar gescheiden door de voor wisselspanning aan de massa liggende basis van de transistor. Daardoor wordt een wederzijdse beïnvloeding volledig uitgesloten.
De koppelfactor
De koppelfactor wordt bepaald door de verhouding van de condensatoren C1 en C2.
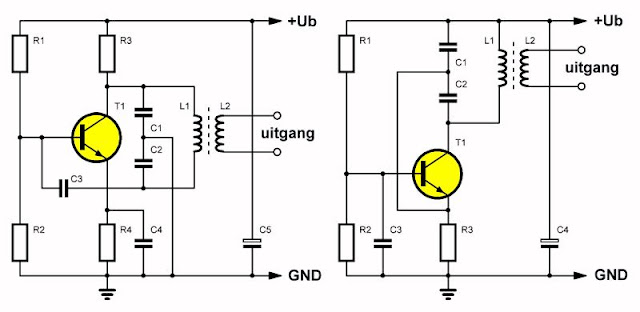 |
| Principe van de Colpitts oscillator, links met emitter-schakeling, rechts met basis-schakeling. (© 2020 Jos Verstraten) |
In de voorgaande schema's wordt gebruik gemaakt van een HF-transformator om het uitgangssignaal uit de schakeling te halen. Dit hoeft niet, in het onderstaande schema is een Colpitts oscillator getekend waarbij het signaal rechtstreeks van de collector van de transistor wordt afgetakt.
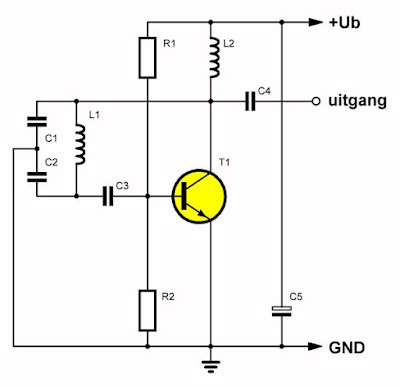 |
| Een Colpitts oscillator met signaaluitgang op de collector. (© 2020 Jos Verstraten) |
De Colpitts oscillator wordt voornamelijk gebruikt voor frequenties boven 10 MHz. U treft deze schakeling regelmatig aan in oscillatoren in kortegolf zenders en ontvangers.
De Hartley oscillator
De werking
Deze schakeling werkt volgens het inductieve driepunt principe. De spoel is nu volgens het spaartrafo principe opgebouwd. De basis en de collector van de transistor zijn verbonden met aftakkingen op de spoel. Dit geldt voor de gemeenschappelijke emitter-schakeling. De volledige kring staat tussen de basis en de collector. De teruggekoppelde spanning wordt via de condensator C2 aan de basis aangeboden. Deze condensator en de voeding vormen voor de signaalspanning immers een kortsluiting.
In de gemeenschappelijke basis-schakeling (rechts) wordt de uitgang via de condensator C2 teruggekoppeld naar de emitter. U kunt de emitterweerstand R3 niet te klein maken, omdat deze weerstand de resonantiekring rechtstreeks belast.
 |
| Principe van de Hartley oscillator, links met emitter-schakeling, rechts met basis-schakeling. (© 2020 Jos Verstraten) |
De koppelfactor wordt nu bepaald door de plaats van de aftakking op de spoel.
Toepassing
U zult de Hartley oscillator voornamelijk aantreffen bij midden en hoge frequenties, zoals bijvoorbeeld in ontvangers.
Capacitieve terugkoppeling oscillator
Inleiding
Bij de besproken schakelingen zijn in- en uitgangsspanningen bij de lage frequenties in fase. Naarmate de frequentie stijgt moet u rekening houden met de basis/emitter-capaciteit. Deze vormt met de ingangsimpedantie van de schakeling een frequentie-afhankelijk netwerk. Dit netwerk introduceert een faseverschuiving tussen de in- en de uitgang. De waarde van deze fasehoek is afhankelijk van de frequentie en van de karakteristieken van de transistor. Van dit verschijnsel wordt gebruik gemaakt in de schakeling van de onderstaande figuur.
De werking
Met de parallel aan de ingangsimpedantie liggende spoel L1 kunt u de fasehoek extra verschuiven, zodat voor een bepaalde frequentie aan de oscillatie voorwaarden wordt voldaan. De terugkoppelcondensator is gedeeltelijk opgebouwd uit de inwendige collector/emitter-capaciteit Cce van de transistor. De parallel aan deze capaciteit geschakelde externe condensator C3 is zeer klein, meestal bedraagt de waarde van dit onderdeel slechts enkele pF. De condensator C4 is noodzakelijk om te verhinderen dat de instelspanning van de transistor via L3 wordt kortgesloten naar de massa. De spoel L2 verhindert dat de signaalspanning afvloeit naar de massa via de lage impedantie van de voeding.
 |
| Principe van de oscillator met capacitieve terugkoppeling. (© 2020 Jos Verstraten) |
De Wien brug oscillator
Inleiding
De tot nu toe behandelde schakelingen werken allemaal met LC-schakelingen als afgestemd netwerk en zijn ideaal voor het genereren van sinussen in het MHz-bereik. Voor lagere frequenties kunt u deze schakelingen niet meer gebruiken omdat de waarde van de spoelen te groot zou worden.
In laagfrequent oscillatoren zult u dan ook uitsluitend RC-netwerken aantreffen. Een RC-netwerk is in staat een faseverschuiving van maximaal 90° te veroorzaken (althans in theorie). Om aan de oscillatie voorwaarden te voldoen moet u dan ook verschillende RC-netwerken in serie schakelen of gebruik maken van een brugschakeling.
Het basisschema
In de Wien brug oscillator wordt van de twee methode gebruik gemaakt. Zoals uit het schema van de onderstaande figuur volgt, is deze brug samengesteld uit een parallel schakeling van een weerstand en een condensator (R2/C2) en een serie schakeling van identieke componenten (R1/C1).
Als beide weerstanden en beide condensatoren even groot zijn, kunt u de oscillatiefrequentie berekenen uit de formule:
fo = 1 / [2 • π • R • C]
Deze formule is afgeleid van de oscillatie voorwaarde:
R = 1 / [ω • C]
De teruggekoppelde spanning is in fase met de uitgangsspanning over R9.
 |
| Basisschema van een oscillator met een brug van Wien. (© 2020 Jos Verstraten) |
Deze schakeling vereist het gebruik van twee versterkertrappen omdat de 180° fasedraaiing, die door de eerste trap wordt geïntroduceerd, door de tweede trap moet worden opgeheven. In- en uitgang van de versterker moeten dus in fase zijn!
De amplitude voorwaarde
Om aan de amplitude voorwaarde te voldoen moet de totale versterking groter dan drie zijn. Dit is een gevolg van de spanningsdeling die door het netwerk van de brug van Wien tussen de uitgang en de ingang ontstaat en het teruggekoppelde signaal verzwakt.
Met de weerstand R9 kunt u de koppelfactor instellen en de schakeling aan de amplitude voorwaarde (versterking groter dan 3) laten voldoen. Om de waarde van de versterkingsfactor op precies deze drie te stabiliseren moet de schakeling worden voorzien van een aantal terugkoppelingen. Bij de getoonde schakeling (een van de vele) wordt er zowel aan spanning- als aan stroomtegenkoppeling gedaan. De weerstand R3 stabiliseert de eerste versterkertrap, de weerstanden R5 en R10 zorgen voor een stroomtegenkoppeling in de emitterleidingen van de twee halfgeleiders.

Instellen van de frequentie
U kunt de frequentie van de schakeling variëren door ofwel de twee weerstanden ofwel de twee condensatoren van de brug in gelijke mate te veranderen. In de praktijk zal men meestal met behulp van een dubbele omschakelaar een aantal identieke condensatoren in het netwerk opnemen. Als u deze een 1 op 10 verhouding geeft kunt u dan de frequentie van de schakeling met deze schakelaar decadisch instellen. De twee vaste weerstanden worden vervangen door een stereo-potentiometer, waarmee u de frequentie in iedere decade op iedere gewenste waarde kunt instellen.
Een eigen artikel op dit blog
Over de Wien brug oscillator is op dit blog een eigen artikel geschreven met bruikbare voorbeeldschakelingen zie:
https://verstraten-elektronica.blogspot.com/p/sinusgeneratoren.html
De faseverschuiving oscillator
Inleiding
Deze oscillatoren bestaan in de regel uit één versterkertrap waarvan de uitgangsspanning door middel van drie in serie geschakelde RC-netwerken terug wordt gekoppeld naar de ingang.
Het basisschema
Het schema in de onderstaande figuur geeft het basisschema van dit soort oscillatoren. In dit voorbeeld zijn de condensatoren in serie geschakeld tussen de uitgang en de ingang en liggen de weerstanden naar de massa
geschakeld, maar er zijn ook schakelingen waar dit omgekeerd is.
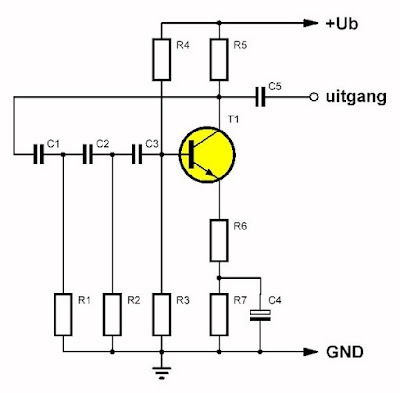 |
| Basisschema van de faseverschuiving oscillator. (© 2020 Jos Verstraten) |
De RC-netwerken werken als frequentie-afhankelijke spanningsdelers, waarbij de spanning op het knooppunt tussen weerstand en condensator een faseverschuiving tussen 0° en 90° heeft ten opzichte van de ingangsspanning. De mate van verschuiving is afhankelijk van de waarde van de onderdelen en van de frequentie.
Bij een transistortrap, geschakeld in de gemeenschappelijke emitter configuratie, bestaat er een faseverschuiving van 180° tussen de ingangsspanning op de basis en de uitgangsspanning op de collector. Het faseverschuivende netwerk moet daar dus nog eens 180° aan toevoegen om aan de oscillatie voorwaarde te kunnen voldoen. Voor het bereiken van deze 180° zijn drie RC-netwerken noodzakelijk. In de praktijk kiest men drie identieke weerstanden en drie identieke condensatoren.
De RC-kringen wordt belast door de volgende RC-kring. De faseverschuivingen van de drie netwerken zijn daardoor niet even groot. De frequentie waarbij aan de fase voorwaarde wordt voldaan hangt af van de manier waarop het netwerk is samengesteld.
Bij het systeem van de bovenstaande figuur wordt de frequentie gegeven door:
fo = 1 / [15,4 • R • C]
Een alternatieve schakeling
De onderstaande figuur geeft een schema waarbij de condensatoren en weerstanden van plaats zijn verwisseld. Bij dit systeem wordt de frequentie gegeven door de formule:
fo = 1 / [2,56 • R • C]
De schakeling wordt gestabiliseerd door de niet ontkoppelde emitterweerstand. Door de waarde van deze weerstand te variëren kunt u de versterking van de trap instellen. Door in serie met een van de RC-netwerken een instelbare weerstand op te nemen (R4 in de figuur) kunt u de frequentie in geringe mate instellen.
 |
| Een alternatieve schakeling volgens het faseverschuiving principe. (© 2020 Jos Verstraten) |
Het is vrij moeilijk de frequentie bij deze schakelingen in een groot bereik te regelen. U moet immers gebruik moeten maken van drie draaibare condensatoren, die mechanisch zijn gekoppeld. Het is namelijk niet mogelijk de waarde van de weerstanden over een groot bereik te veranderen omdat daardoor de gelijkspanningsinstelling van de trap in het gedrang komt. U zult deze schakeling dan ook hoofdzakelijk tegenkomen op plaatsen waar een sinusoscillator met vaste frequentie nodig is.
De kristal oscillator
Inleiding
In kristalgestuurde oscillatoren wordt het frequentiebepalend LC-netwerk vervangen door een kristal. Deze onderdelen hebben een door hun fysische kenmerken bepaalde zeer stabiele resonantiefrequentie. De maximale afwijking bedraagt minder dan 0,0001%. Deze elementen lenen zich dus uitstekend in die toepassingen waar u over een signaal met een zeer stabiele frequentie moet beschikken. De gegenereerde frequentie is daarbij volledig onafhankelijk van de voedingsspanning, de belasting, de terugkoppeling en de omgevingstemperatuur.
Wat zijn kristallen?
Kristallen zijn kleine plaatjes siliciumdioxide (Si02), die ofwel kunstmatig worden vervaardigd of geslepen uit natuurlijke kristallen. Op twee tegenover elkaar liggende vlakken worden elektrische contacten aangebracht. Verbindt u deze contacten met een wisselspanning, dan zal het kristal vanwege de piëzo-elektrische eigenschappen gaan trillen. De frequentie van deze trillingen wordt bepaald door de fysische eigenschappen van het plaatje, door zijn samenstelling, afmetingen en manier waarop het geslepen is.
Het equivalent schema van een kristal
U kunt een equivalent schema van een kristal opstellen, zie de onderstaande figuur links. U kunt hieruit afleiden dat een kristal elektrisch te vergelijken is met een afgestemde kring met LC-samenstelling. Het grote voordeel is dat de kwaliteitsfactor van een kristal vele malen groter en dus beter is dan deze van met 'echte' inducties en condensatoren samengestelde afgestemde kringen.
De impedantie/frequentie-karakteristiek
In de figuur is rechts de impedantie/frequentie-karakteristiek van een kristal voorgesteld. Er bestaat één frequentie waarbij de impedantie minimaal is, deze noemt men de serie-resonantie frequentie fs. Bij de parallel-resonantie frequentie fp gaat de impedantie van het kristal naar een maximale waarde. De serie-resonantie is steeds lager dan de parallel-resonantie.
 |
| Equivalent schema en frequentiekarakteristiek van een kristal. (© 2020 Jos Verstraten) |
In principe wordt de resonantiefrequentie bepaald door de afmetingen van het kristalplaatje. Hoe kleiner het plaatje, hoe hoger de frequentie. Nu bestaan er natuurlijk technologische grenzen aan de minimale afmetingen van een kristal. Gelukkig kunt u een kristal ook laten oscilleren op de oneven hogere harmonischen van de eigen resonantiefrequentie. Van dit verschijnsel maakt men gebruik bij kristal oscillatoren van meer dan 30 MHz. U kunt bijvoorbeeld een 30 MHz kristal laten oscilleren op de derde, vijfde of zevende harmonische en zodoende stabiele frequenties van 90, 150 of 210 MHz opwekken.
De basisschakelingen
U kunt in theorie alle schakelingen die gebruik maken van een LC-resonantiekring ook gebruiken voor het samenstellen van een kristal oscillator. Tóch heeft men een aantal schakelingen specifiek ontwikkeld met een kristal als frequentiebepalend element:
- De Heegner oscillator.
- De Fränklin oscillator.
- De Pierce oscillator.
De Heegner oscillator
De onderstaande figuur geeft het basisschema van een Heegner oscillator. Het kristal wordt hierbij als serie-resonator gebruikt. De waarde van de weerstanden R1 en R2 moet gelijk of kleiner zijn dan de serieweerstand van het kristal zélf.
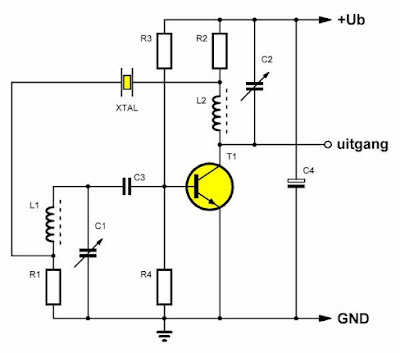 |
| Het basisschema van een Heegner oscillator. (© 2020 Jos Verstraten) |
In de onderstaande figuur ziet u het basisschema van de Fränklin oscillator. In deze tweetrap schakeling wordt de terugkoppeling gesloten via condensator C3, condensator C2 en het kristal XTAL. Ook bij deze schakeling trilt het kristal op zijn serie-resonantiefrequentie.
 |
| De basis uitvoering van de Fränklin oscillator. (© 2020 Jos Verstraten) |
FET's hebben een hoge ingangsimpedantie en een lage ingangscapaciteit. Dit heeft als voordeel dat het kristal nauwelijks belast wordt en de hoge kwaliteitsfactor van het kristal zélf in de schakeling gehandhaafd kan blijven.
De onderstaande figuur geeft het basisschema van een Pierce oscillator. Deze schakeling heeft als groot voordeel dat u kristallen in een breed frequentiebereik in de schakeling kunt opnemen zonder dat u iets aan het schema moet wijzigen.
 |
| De basis uitvoering van de Pierce oscillator. (© 2020 Jos Verstraten) |
Hoewel de resonantiefrequentie van een kristal vast ligt door de constructieve en fysische eigenschappen van het kristalplaatje kunt u deze grootheid toch in geringe mate wijzigen door in serie met of parallel over het kristal een condensatortrimmer of een afstembare spoel op te nemen. Dat kan door de ferriet kern min of meer in of uit de spoel te draaien. Door deze schakelingen kunt u de fabricagetoleranties op de eigen frequentie van het kristal compenseren, hetgeen natuurlijk bij een aantal voor de hand liggende toepassingen absoluut noodzakelijk is. Denk maar aan een elektronisch uurwerk, waar iedere minimale afwijking van de theoretische frequentie op de lange termijn ontoelaatbare tijdfouten tot gevolg heeft.
 |
| Het afregelen van een kristal in een oscillator schakeling. (© 2020 Jos Verstraten) |
U moet er echter wel rekening mee houden dat u aan de onderdelen die voor het 'trimmen' van de kristalfrequentie worden gebruikt de hoogst mogelijke stabiliteitseisen moet stellen!
Soldeerbout met temperatuurindicatie


