|
Kristallen worden in vrijwel ieder elektronisch apparaat gebruikt. Zij vormen het hart van de klokoscillator van de microcontroller of microprocessor in het apparaat.
|
Inleidende begrippen
Frequentiereferenties
Voor diverse doeleinden moet u in de elektronica beschikken over signalen met een zeer stabiele frequentie. Te denken valt daarbij aan:
- Oscillatoren voor chronometers
- Tijdbasissen in digitale frequentiemeters
- Referenties voor frequentie synthesizers
- Lokale oscillatoren in heterodyne ontvangers
- Klokoscillatoren in microprocessorsystemen
- Tijdbasis in digitale oscilloscopen
Met RC-oscillatoren is een frequentiestabiliteit tot 0,1 % haalbaar, met LC-oscillatoren is 0,01 % mogelijk. Als u een nog grotere frequentiestabiliteit nodig hebt is een kristaloscillator de enige oplossing. Ondanks dat het kristal, zoals dat op dit moment wordt gefabriceerd, een zeer oud elektronisch onderdeel is, neemt de belangrijkheid ervan nog steeds toe.
Terminologie
De onderdelen die in dit artikel worden besproken worden algemeen aangeduid met de term 'kristal'. Soms treft men ook de term 'kwartskristal' aan, hoewel de kans dat het onderdeel écht is gemaakt van kwarts tegenwoordig uiterst klein is. In het Engels wordt het woord 'crystal' gebruikt, vaak afgekort tot 'xtal'. Soms worden 'piëzoceramische resonatoren' en 'stemvorken' ook kristallen genoemd, hoewel er duidelijk verschillen tussen deze soorten onderdelen bestaan.
Fabricage van een kristal
Bepaalde natuurlijke materialen zoals kwarts vertonen een piëzo-elektrisch effect. Wanneer een plaatje van zo'n materiaal wordt samengedrukt of uitgerekt ontstaat er over het materiaal een elektrische spanning. Als een elektrische spanning over het materiaal wordt gezet dan zal dit samengedrukt of uitgerekt worden. Het materiaal reageert dus op een wisselend elektrisch veld door het uitvoeren van een periodieke beweging. De frequentie waarmee dit gebeurt is afhankelijk van de fysische eigenschappen van het materiaal, met name de dikte van het plaatje.
Door deze eigenschap is het mogelijk een materiaal met piëzo-elektrische eigenschappen te gebruiken voor het genereren van een wisselspanning met een zeer constante frequentie. Als u over een plaatje materiaal met dergelijke eigenschappen een breedbandige ruisspanning zet, dan zal het plaatje één frequentie uit dit signaal gaan versterken. Dat is de frequentie waarop het plaatje maximaal gaat trillen. Door dit trillen en door het genoemde effect zal er over het plaatje namelijk een vrij grote spanning ontstaan waarvan de frequentie gelijk is aan de resonantiefrequentie van het plaatje.
Het piëzo-elektrische effect
Het piëzo-elektrische effect werd in 1880 ontdekt door Jacques en Pierre Curie en werd voor het eerst gebruikt voor het regelen van de frequentie van een elektronische oscillator in 1921 door W. Gady.
Natuurlijke kristallen
Er bestaan ongeveer 3.000 minerale grondstoffen die piëzo-elektrische eigenschappen hebben. De meeste mineralen zijn in hun natuurlijke vorm echter volstrekt onbruikbaar vanwege onzuiverheden die in het materiaal aanwezig zijn. Voor de fabricage van kwartskristallen werd vroeger gebruik gemaakt van ruw kwarts (SiO2), gedolven in Brazilië. Dit kwarts werd gesmolten onder zeer hoge druk en nadien uitgekristalliseerd. Er ontstaan dan grote hexagonale kristallen met de typische vorm die in de onderstaande figuur is geschetst.
 |
| Hexagonale kwartkristallen. (© AliExpress) |
Synthetische kristallen
Tegenwoordig wordt echter hoofdzakelijk gebruik gemaakt van synthetische kristallen. Deze bevatten veel minder kristalfouten en zijn veel zuiverder dan de natuurlijke materialen. Een paar in het laboratorium gemaakte stoffen die ook voor de productie van elektronische kristallen gebruikt kunnen worden zijn:
- Gallium arsenide
- Bismuth/germanium oxide
- Lithium boraat
- Silicium/zink oxide
- Zirconium titanaat
- Gallium fosfaat
Het versnijden van het kristal
De snede (cut)
Uit een basiskristal kunnen duizenden dunne plaatjes worden gezaagd. Deze plaatjes vormen de basis van de elektronische onderdelen die men kristallen noemt. De eigenschappen van het plaatje hangen niet alleen af van de dikte, maar ook van de hoek (de snede of cut) waaronder de plaatjes uit het basiskristal worden gezaagd. Er zijn in de loop der tijd tientallen sneden uitgeprobeerd die ieder iets andere specificaties aan het kristal geven. Dat gaat dan voornamelijk over de verouderingsverschijnselen, de thermische stabiliteit en de frequentie stabiliteit.
De dikte van het plaatje bepaalt de uiteindelijke resonantiefrequentie van het kristal, de snede bepaalt voornamelijk de mate waarin de resonantiefrequentie afhankelijk is van de temperatuur.
In de onderstaande figuur is een overzicht gegeven van de meest gebruikte sneden die worden toegepast.
 |
| Diverse sneden door kristallen. (© 2022 Jos Verstraten) |
De AT-snede
Dit is de oudste snede die reeds in 1934 werd toegepast en ook nu nog de vaakst toegepaste snede is. De AT-snede maakt een hoek van ongeveer 35 graden met de optische lengte-as van het basiskristal. Met deze snede kunnen kristallen worden gemaakt met resonantiefrequenties tussen 0,5 MHz en 300 MHz. In de meeste gevallen worden de gesneden plakjes tot cirkelvormige plaatjes verwerkt die de basis vormen van de meeste kristallen in de standaard behuizingen van de HC-reeks (lees verder).
De Y-snede
Deze snede wordt voornamelijk toegepast bij kristallen die gebruikt worden voor het meten van temperaturen. Deze snede heeft namelijk een temperatuurscoëfficiënt die lineair is in functie van de temperatuur. Zo zal een kristal, gesneden volgens de Y-snede en met een basisfrequentie van 10 MHz, een lineair frequentieverloop hebben van 800 Hz per graad celsius over een breed temperatuurbereik. Schakelingen met een dergelijk kristal worden 'TSXO' genoemd, letterwoord van 'Temperature Sensing Xtal Oscillator'.
De X-snede
Deze snede werd in 1921 door Walter Guyton Cady toegepast in de oudste kristaloscillatoren en in een 50 kHz kristal in een van de eerste kristal-klokken, in 1927 ontworpen door Henry Bishop Horton en Warren Marrison.
Overige sneden
Naast de meest toegepaste AT- en Y-sneden worden er ook nog een heleboel andere sneden gebruikt, zoals de DT-, de BT- en de CT-sneden. Deze worden voornamelijk toegepast voor het fabriceren van kristallen met zeer lage frequenties, maar hebben slechte temperatuur karakteristieken.
De TTC-snede
Een speciale vermelding verdient de TTC-snede, de zogenaamde 'Thermal Transiënt Compensated'-snede. Deze heeft een slechte stabiliteit bij lage temperaturen maar een zeer hoge stabiliteit bij hoge temperaturen. Dergelijke kristallen zijn dus uitermate geschikt voor inbouw in kritische thermostaat geregelde oscillatoren waarbij het kristal op een constante vrij hoge temperatuur wordt gehouden door een elektronische regelschakeling. Dergelijke schakelingen worden 'TCXO' genoemd, letterwoord van 'Temperature Compensated Xtal Oscillator'.
De temperatuurscoëfficiënt van de sneden
De afhankelijkheid van de temperatuurscoëfficiënt van de snedehoek wordt gedemonstreerd aan de hand van de grafiek van de onderstaande figuur.
 |
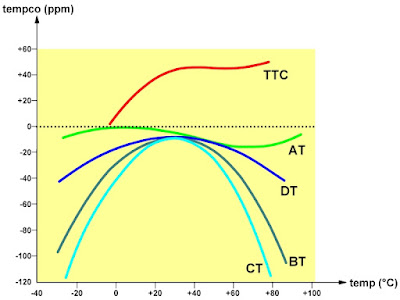| De temperatuurscoëfficiënt van diverse sneden. (© 2022 Jos Verstraten) |
Omdat in de praktijk meestal wordt gewerkt met de AT-snede worden de temperatuur eigenschappen van deze kristallen nader besproken. Zeer kleine variaties in de snedehoek hebben zeer grote invloed op de temperatuurscoëfficiënt. Dit wordt mooi gedemonstreerd in de onderstaande grafiek. De getallen in de grafieken geven de snede-afwijking in graad-minuten aan. Hieruit blijkt duidelijk dat zelfs de geringste afwijking van de ideale snedehoek een grote invloed heeft op de temperatuurscoëfficiënt!
 |
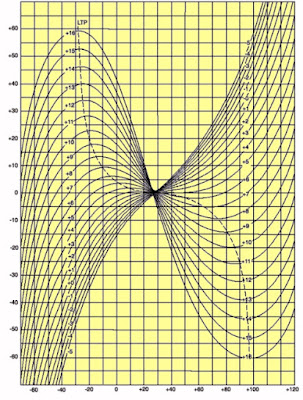Invloed van de snede-hoek op de tempco bij AT-kristallen. |
De frequentie in functie van de snededikte
De resonantiefrequentie van een kristal wordt in eerste instantie bepaald door de snedehoek en door de dikte van het uitgezaagde plaatje. Het zal duidelijk zijn dat de frequentie omgekeerd evenredig is met de dikte van het plaatje! Voor de AT-snede geldt bijvoorbeeld dat de frequentie ongeveer gelijk is aan 1,675 MHz voor een plaatje met een dikte van 1 mm. Nu is kwarts een zeer hard materiaal dat zeer moeilijk te bewerken is. Door het zagen en slijpen van de plaatjes wordt de oppervlaktestructuur van het kristal beschadigd. Dit wordt verholpen door de oppervlakken chemisch te etsen of mechanisch te polijsten. Door deze nabewerkingen zal het plaatje echter iets dunner worden, waardoor de resonantiefrequentie stijgt. Dit kan verholpen worden door een dun goudlaagje op het plaatje op te dampen. Een goudlaag van één atoom dik heeft een invloed van 2 parts per million op de resonantiefrequentie van het plaatje.
De constructie van kristallen
Kristallen met aansluitdraadjes
Kristallen met aansluitdraadjes worden geleverd in standaard behuizingen met een HC-code. Nadat de ronde plaatjes op de juiste dikte zijn gebracht worden deze ingebouwd in metalen of glazen behuizingen. Het plaatje wordt volgens de onderstaande figuur ingeklemd tussen twee elektroden die ieder op een steundraad zijn gelast. De steundraden gaan via een geïsoleerde voetplaat naar buiten. De voetplaat wordt in een metalen of glazen behuizing gemonteerd. De eigenschappen van het praktische kristal worden in niet geringe mate bepaald door de behuizing.
 |
De constructie van een HC-kristal. (© 2022 Jos Verstraten) |
Metalen behuizing
Bij deze behuizing wordt de metalen voetplaat door middel van weerstandslassen bevestigd op een kapje van vernikkeld plaatstaal. Mogelijke problemen als gevolg van kortsluitingen tussen voetplaat en aansluitpennen worden voorkomen door stuksgewijze controle van de stalen voetplaatjes. De hermetische behuizing wordt volledig vertind om corrosie- en soldeerproblemen te vermijden.
De belangrijkste voordelen van de metalen behuizing zijn de lage kostprijs en de eenvoudige toepassing in automatische soldeermachines. Nadeel is echter dat de metalen kap in de loop der tijd stoffen kan afscheiden die zich op het plaatje gaan hechten. Dat proces noemt men het verouderen van het kristal. Gevolg is dat de frequentie van het kristal gaat verlopen en eigenschappen zoals de kwaliteitsfactor nadelig beïnvloed kunnen worden.
Glazen behuizing
De hermetisch gesloten glazen behuizing is in de loop der jaren aanzienlijk geperfectioneerd. Bij de inbouw wordt in een groef van de glazen voetplaat een ringetje van Kovar aangebracht. Na het aanbrengen van de glazen ballon wordt het geheel verhit door een HF-generator, waarbij beide onderdelen onverbrekelijk aan elkaar worden gelast.
Hoewel een kristal in een glazen behuizing veel duurder is dan een in een metalen omhulling heeft deze constructie voordelen:
Tegenwoordig wordt voornamelijk de behuizing HC-49/U gebruikt. Deze is met haar hoogte van 4 mm zo laag dat zij zelfs onder een open IC-voetje past. Wie wel eens Chinese bouwpakketjes heeft gesoldeerd weet dat de ontwerpers daarvan vaak gebruik maken van deze eigenschap en het klokkristal met de twee bijbehorende condensatortjes onder de voet van de microcontroller plaatsen.
Natuurlijk kan het plaatje dan niet meer rechtop in de behuizing worden gemonteerd. Men past dan de onderstaande fabricage toe, waarbij het plaatje horizontaal in de platte behuizing vrijwel op de pennetjes ligt. Het plaatje is nu niet rond, maar rechthoekig en is aan weerszijden voorzien van een opgedampte metalen laag, het zogenaamde 'electrode plating'. Deze lagen zijn met elektrische geleidende lijm gefixeerd op twee steuntjes die eerst op de aansluitdraadjes werden gelast. Deze draadjes gaan via in de behuizing ingesmolten glaspareltjes naar de buitenwereld.
SMD-kristallen
De HC-49 behuizing wordt ook aangeboden in een SMD-uitvoering, zie de onderstaande figuur. Het kristalletje wordt aangebracht op een drager die aan de onderzijde is voorzien van twee koperen strips die iets uitsteken. Deze strips kunt u op de pad's van de print solderen.
Daarnaast kunt u tegenwoordig ook 'echte' SMD-kristallen kopen met veel kleinere afmetingen dan de aangepaste HC-49 types. Er zijn diverse uitvoeringen op de markt, maar de onderstaande afbeelding geeft de uitvoering SMD3225 die u vaak zult tegenkomen op de pagina's van postorder bedrijven. Deze kristalletjes kosten nog geen twintig eurocent! De soldeervlakjes 2 en 4 zijn verbonden met de metalen behuizing van het kristal.
Montage van kristallen
Hoewel het in principe mogelijk is thru-hole kristallen rechtstreeks in een print te solderen wordt aanbevolen gebruik te maken van de speciale voetjes die door diverse fabrikanten worden geleverd. In de onderstaande figuur ziet u zo'n voetje dat door Fischer Elektronik wordt gemaakt. Zo'n voetje is vrij prijzig vergeleken met de prijs van het kristal zélf, namelijk het kost iets meer dan één euro. Deze voetjes kunt u op de print solderen, de kristallen kunnen nadien net zoals een IC in de voetjes worden geprikt.
Verouderen van een kristal
De karakteristieken van een kristal veranderen naarmate het onderdeel ouder wordt. Een van de belangrijkste redenen is al gegeven: het emigreren van verontreinigingen van de behuizing naar het kristalplaatje. Daarnaast zal er ook migratie plaats vinden van het oppervlak van het plaatje naar de behuizing, waardoor het plaatje dus iets dunner wordt. Tot slot zullen de trillingskarakteristieken van het plaatje langzaam veranderen. Het lijkt alsof het plaatje 'stijver' wordt naarmate het langer trilt. Als u al deze effecten bij elkaar optelt komt u uit op een gemiddeld verouderingseffect van ongeveer 10 parts per million per jaar uit voor kristallen in metalen behuizingen en 2 parts per million per jaar voor onderdelen in glazen behuizingen. Dit verouderingseffect is, zoals blijkt uit de grafiek van de onderstaande figuur, geen lineair effect. Het effect is het sterkst in de eerste levensmaanden van het kristal.
Het zal duidelijk zijn dat het verouderingseffect tot gevolg heeft dat zeer kritische kristaloscillatoren, zoals bijvoorbeeld toegepast in zeer nauwkeurige digitale frequentiemeters, regelmatig geijkt moeten worden.
Omgevingseffecten
De levensduur is niet de enige factor die de nauwkeurigheid van een kristal beïnvloedt. Wij noemen alle factoren die de frequentie-nauwkeurigheid kunnen aantasten:
Equivalent schema van een kristal
Van ieder elektronisch onderdeel kunt u een zogenaamd equivalent schema opstellen. Dat is een serie/parallel-schakeling van weerstanden, condensatoren en spoelen die de elektrische eigenschappen van het onderdeel precies nabootst. Het equivalent schema en het symbool van een kristal zijn getekend in de onderstaande figuur. De vier elementen vertegenwoordigen:
- L1, de resonerende massa van het kristalplaatje
- C1, de elastische compliantie van het plaatje
- R1, de wrijvingsverliezen tijdens het oscilleren
- C0, de capaciteit van het kristalplaatje en de capaciteit van de behuizing.
Glazen behuizing
De hermetisch gesloten glazen behuizing is in de loop der jaren aanzienlijk geperfectioneerd. Bij de inbouw wordt in een groef van de glazen voetplaat een ringetje van Kovar aangebracht. Na het aanbrengen van de glazen ballon wordt het geheel verhit door een HF-generator, waarbij beide onderdelen onverbrekelijk aan elkaar worden gelast.
Hoewel een kristal in een glazen behuizing veel duurder is dan een in een metalen omhulling heeft deze constructie voordelen:
- Glas is chemisch inert en scheidt geen stoffen af die het kristalplaatje en de elektroden kunnen aantasten.
- De glazen ballon kan volledig ontgast worden bij temperaturen tot 500 graden onder een hoog vacuüm.
- Glas heeft een kleinere doorlatendheid dan metaal, daardoor is de hermetische afsluiting perfect en kunnen gassen niet doordringen tot het kristalplaatje.
- Glazen kristallen kunnen gebruikt worden tot werktemperaturen van 300 graden.
De genormaliseerde HC-behuizingen voor thru-hole kristallen
Kristallen in metalen behuizingen met aansluitdraadjes (thru-hole) worden aangeboden in genormaliseerde behuizingen. Deze worden meestal volgens de Amerikaanse codering HC-xx/U genoemd, waarbij x een getal is dat de afmetingen bepaalt. In de onderstaande figuur zijn de afmetingen van de vaakst gebruikte HC-behuizingen samengevat.
 |
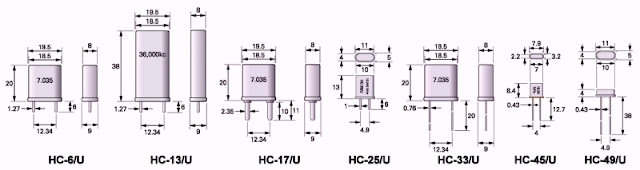| De afmetingen van de HC-behuizingen. (© 2022 Cryptomuseum/Jos Verstraten) |
Tegenwoordig wordt voornamelijk de behuizing HC-49/U gebruikt. Deze is met haar hoogte van 4 mm zo laag dat zij zelfs onder een open IC-voetje past. Wie wel eens Chinese bouwpakketjes heeft gesoldeerd weet dat de ontwerpers daarvan vaak gebruik maken van deze eigenschap en het klokkristal met de twee bijbehorende condensatortjes onder de voet van de microcontroller plaatsen.
Natuurlijk kan het plaatje dan niet meer rechtop in de behuizing worden gemonteerd. Men past dan de onderstaande fabricage toe, waarbij het plaatje horizontaal in de platte behuizing vrijwel op de pennetjes ligt. Het plaatje is nu niet rond, maar rechthoekig en is aan weerszijden voorzien van een opgedampte metalen laag, het zogenaamde 'electrode plating'. Deze lagen zijn met elektrische geleidende lijm gefixeerd op twee steuntjes die eerst op de aansluitdraadjes werden gelast. Deze draadjes gaan via in de behuizing ingesmolten glaspareltjes naar de buitenwereld.
 |
Het interne van een HC-49/U kristal. (© 2022 Jos Verstraten) |
SMD-kristallen
De HC-49 behuizing wordt ook aangeboden in een SMD-uitvoering, zie de onderstaande figuur. Het kristalletje wordt aangebracht op een drager die aan de onderzijde is voorzien van twee koperen strips die iets uitsteken. Deze strips kunt u op de pad's van de print solderen.
 |
| Een HC-49 kristal in SMD-uitvoering. (© Conrad Electronic) |
Daarnaast kunt u tegenwoordig ook 'echte' SMD-kristallen kopen met veel kleinere afmetingen dan de aangepaste HC-49 types. Er zijn diverse uitvoeringen op de markt, maar de onderstaande afbeelding geeft de uitvoering SMD3225 die u vaak zult tegenkomen op de pagina's van postorder bedrijven. Deze kristalletjes kosten nog geen twintig eurocent! De soldeervlakjes 2 en 4 zijn verbonden met de metalen behuizing van het kristal.
 |
| Een 'echt' SMD-kristal in SMD3225 uitvoering. (© Alibaba) |
Montage van kristallen
Hoewel het in principe mogelijk is thru-hole kristallen rechtstreeks in een print te solderen wordt aanbevolen gebruik te maken van de speciale voetjes die door diverse fabrikanten worden geleverd. In de onderstaande figuur ziet u zo'n voetje dat door Fischer Elektronik wordt gemaakt. Zo'n voetje is vrij prijzig vergeleken met de prijs van het kristal zélf, namelijk het kost iets meer dan één euro. Deze voetjes kunt u op de print solderen, de kristallen kunnen nadien net zoals een IC in de voetjes worden geprikt.
 |
Een printvoetje voor een kristal. (© Fischer Elektronik) |
Elektrische eigenschappen van kristallen
Verouderen van een kristal
De karakteristieken van een kristal veranderen naarmate het onderdeel ouder wordt. Een van de belangrijkste redenen is al gegeven: het emigreren van verontreinigingen van de behuizing naar het kristalplaatje. Daarnaast zal er ook migratie plaats vinden van het oppervlak van het plaatje naar de behuizing, waardoor het plaatje dus iets dunner wordt. Tot slot zullen de trillingskarakteristieken van het plaatje langzaam veranderen. Het lijkt alsof het plaatje 'stijver' wordt naarmate het langer trilt. Als u al deze effecten bij elkaar optelt komt u uit op een gemiddeld verouderingseffect van ongeveer 10 parts per million per jaar uit voor kristallen in metalen behuizingen en 2 parts per million per jaar voor onderdelen in glazen behuizingen. Dit verouderingseffect is, zoals blijkt uit de grafiek van de onderstaande figuur, geen lineair effect. Het effect is het sterkst in de eerste levensmaanden van het kristal.
Het zal duidelijk zijn dat het verouderingseffect tot gevolg heeft dat zeer kritische kristaloscillatoren, zoals bijvoorbeeld toegepast in zeer nauwkeurige digitale frequentiemeters, regelmatig geijkt moeten worden.
 |
| Het verouderen van een kristal. (© 2022 Jos Verstraten) |
Omgevingseffecten
De levensduur is niet de enige factor die de nauwkeurigheid van een kristal beïnvloedt. Wij noemen alle factoren die de frequentie-nauwkeurigheid kunnen aantasten:
- Temperatuur
De frequentie van een kristaloscillator is afhankelijk van de temperatuur en u moet daar in de praktijk terdege rekening mee houden. Voor zeer kritische toepassingen moet u de temperatuur van het onderdeel stabiliseren, zo niet is er van een echte frequentiestandaard geen sprake! - Veroudering
Heeft tot gevolg dat u ook een temperatuur gestabiliseerde oscillator regelmatig moet ijken. - Mechanische schokken
Als een kristal wordt onderworpen aan forse versnellingen, dus mechanische schokken, kan de frequentie van het onderdeel verlopen. Dit effect treedt niet alleen op gedurende de schokken, maar kan blijvende afwijkingen van ppm's tot gevolg hebben. Kristallen moet u dus voorzichtig behandelen en niet te vaak laten vallen! - Omdraaien van het kristal
Hoe gek het ook lijkt, als u een kristal omdraait in zijn voetje kan de frequentie veranderen! Dit heeft een invloed van enige parts per million op de resonantiefrequentie en schijnt een gevolg te zijn van de invloed van de aardse zwaartekracht op het kristalplaatje.
Equivalent schema van een kristal
Van ieder elektronisch onderdeel kunt u een zogenaamd equivalent schema opstellen. Dat is een serie/parallel-schakeling van weerstanden, condensatoren en spoelen die de elektrische eigenschappen van het onderdeel precies nabootst. Het equivalent schema en het symbool van een kristal zijn getekend in de onderstaande figuur. De vier elementen vertegenwoordigen:
- L1, de resonerende massa van het kristalplaatje
- C1, de elastische compliantie van het plaatje
- R1, de wrijvingsverliezen tijdens het oscilleren
- C0, de capaciteit van het kristalplaatje en de capaciteit van de behuizing.
 |
| Symbool en equivalent schema van een kristal. (© 2022 Jos Verstraten) |
De impedantie-karakteristiek van een kristal
Een kristal bestaat uit twee LC-kringen, een seriekring opgebouwd uit C1 en L1 en een parallelkring samengesteld uit C0 en L1. Het zal duidelijk zijn dat een kristal zich gedraagt zoals iedere andere serie/parallel-schakeling van spoelen en condensatoren. Als u het kristal aansluit op een hoogfrequent generator en de impedantie van het onderdeel meet voor verschillende frequenties, dan ontstaat de karakteristiek van de onderstaande figuur. Bij een bepaalde frequentie fs treedt een minimale impedantie op. Deze frequentie komt overeen met de seriële resonantiefrequentie van het kristal. Bij een iets hogere frequentie fp treedt een maximale impedantie op. Deze frequentie is de parallelle resonantiefrequentie van het onderdeel. De fs wordt bepaald door de serieschakeling van L1 en C1, de fp door het parallel schakelen van C0 aan deze kring.
Let op dat de verticale impedantie-as logaritmisch is ingedeeld en dat er dus een vrij groot verschil bestaat tussen de seriële en parallele resonantie-impedanties van een kristal.|
De resonantiefrequenties
Men kan, volgens wiskundige wetten, de exacte waarde van beide resonantiefrequenties berekenen uit de waarden van de onderdelen L1, C0 en C1. Deze formules zijn gegeven in de bovenstaande figuur. Bij de seriële resonantie treedt een fasedraaiing op van nul graden. Dat is een belangrijk gegeven bij het ontwerpen van oscillatorschakelingen! Uit het equivalent schema en de resonantieformules blijkt duidelijk dat u de waarde van de parallel resonantie kunt beïnvloeden door het schakelen van een condensator over het kristal. Dan wordt de waarde van C0 immers aangepast en dit onderdeel bepaalt de fp.
Nu zal er in een praktische schakeling altijd een bepaalde parallelle capaciteit worden geïntroduceerd. Kristallen die worden gespecificeerd door hun parallelle resonantie worden altijd gekalibreerd voor een specifieke waarde van de parallelle externe capaciteit. In de meeste gevallen bedraagt deze extern aan te brengen capaciteit 20 tot 30 pF. De invloed van deze externe capaciteit op de frequentienauwkeurigheid van de oscillator is vrij groot. Een verandering van slechts 0,5 pF op een waarde van 20 pF heeft reeds een frequentiefout van ongeveer 10 parts per million tot gevolg. U kunt dus niet zomaar gelijk welke ceramische condensator parallel schakelen, maar moet zoeken naar onderdelen met minimale temperatuurscoëfficiënt.
De diverse trillingsmodi
Kristallen kunnen zowel op hun seriële als op hun parallelle resonantiefrequentie worden ingesteld. Een en ander is afhankelijk van de schakeling waarin u het onderdeel opneemt. Omdat de frequentie van de parallelle trillingsmodus eenvoudig is te variëren door het parallel schakelen van een condensatortrimmer zal men in de meeste gevallen van deze modus gebruik maken. Kristallen kunnen echter ook op hun harmonische frequenties worden afgestemd. Dat noemt men het 'overtonen' van het kristal. Dat is het rechtstreekse gevolg van de uitgebreide impedantiegrafiek van een kristal, voorgesteld in de onderstaande figuur. In deze grafiek is niet alleen het impedantieverloop weergegeven, maar ook het inductieve of capacitieve gedrag van het kristal. Duidelijk blijkt dat na de punten fs en fp er nog een heleboel frequenties terug te vinden zijn waarbij het kristal een minimale of maximale impedantie heeft. In principe is het mogelijk het kristal op al deze frequenties te laten trillen.
In de praktijk maakt men echter alleen gebruik van de derde en vijfde harmonischen.
'Spurious' frequenties
Na de fp pieken ziet u in de bovenstaande grafiek nog wat kleine impedantie-piekjes. Die piekjes ontstaan bij frequenties die men 'spurious' (onecht) noemt. Hoewel de meeste spurious piekjes enkele tientallen kHz boven de gewenste resonantie liggen, is hun temperatuurscoëfficiënt veel groter dan deze bij de seriële of parallele pieken fs en fp. Dit heeft tot gevolg dat een goed afgestemde kristaloscillator door het verhogen van de kristaltemperatuur opeens kan gaan oscilleren op een van de 'spurious' frequenties en daarin blijft volharden.
De kwaliteitsfactor van een kristal
De amplitude van de trilling over een kristal zal in iedere praktische schakeling afhangen van de kwaliteitsfactor Q van het onderdeel. Deze factor wordt in hoge mate bepaald door de waarde van de R1 uit het equivalent schema.
De kwaliteit van een kristal in parallelle modus wordt gedefinieerd door de zogenaamde 'equivalente parallelle weerstand' EPR. Hoe hoger deze EPR, hoe groter de kwaliteit van het kristal is. Bij serieel bedrijf geldt een waarde ESR, de 'equivalente seriële weerstand'. Nu geldt het omgekeerde, hoe kleiner de ESR, hoe groter de kwaliteit van het kristal. De EPR en ESR zijn waarden die moeilijk te voorspellen zijn bij het zagen van de plaatjes uit het moederkristal. Vaak zal de EPR meer dan een factor vijf verschillen tussen identieke kristaltypen. Alle kristallen van een bepaald type hebben uiteraard wel een minimale EPR en het is deze waarde die u moet aanhouden bij het ontwerpen van schakelingen.
Het gedissipeerde vermogen
Als een kristal wordt toegepast in een oscillator zal er over het onderdeel een bepaalde wisselspanning ontstaan. Deze spanning zal in de EPR of ESR een bepaald vermogen dissiperen. Als er een te grote spanning over het kristal ontstaat zal het gedissipeerde vermogen te groot worden. Dat heeft drie nadelige gevolgen:
In het algemeen raadt men onderstaande uitsturingsvermogens aan in het kristal:
- 1 MHz tot 3 MHz op grondtoon: 1,0 mW
- 3 MHz tot 20 MHz op grondtoon: 0,5 mW
- Meer dan 20 MHz op grondtoon: 0,2 mW
- 20 MHz tot 140 MHz op harmonischen: 0,5 mW
Temperatuurcompensatie met thermistoren
De frequentie van een kristal is afhankelijk van de temperatuur. Als deze factor niet in de hand is te houden is het verstandig een externe compensatie aan te brengen. In de onderstaande figuur is een schakeling getekend waarmee dit mogelijk is. Bij deze schakeling wordt een varicapdiode parallel geschakeld aan het kristal. Dat kan alleen maar als het kristal met één aansluiting aan de massa zit. Het is immers noodzakelijk de varicap in te stellen in sper en dat kan alleen maar als de massa als referentie kan worden gebruikt. Die instelspanning wordt verzorgd vanuit de positieve stabiele referentiespanning +Uref met behulp van een stel thermistoren ofwel temperatuurgevoelige weerstanden. De thermistoren leveren het stuursignaal voor de varicap, deze past zijn capaciteit zodanig aan dat de kring op een constante frequentie blijft oscilleren.
Uiteraard kunt u deze schakelingen niet zélf ontwerpen, tenzij u een temperatuurkamer en oneindig veel geduld ter beschikking hebt. Diverse fabrikanten leveren echter kant-en-klare temperatuurgecompenseerde kristaloscillatoren in één behuizing, waarbij stabiliteiten tot 1 parts per million realiseerbaar zijn.
Voor een beschrijving van oscillatoren met kristallen wordt verwezen naar een ander artikel op dit blog:
Aanklikbare link ➡ Schakelingen: oscillatoren
(Bol.com sponsor advertentie)
Voltcraft LPS1153 labvoeding
Een kristal bestaat uit twee LC-kringen, een seriekring opgebouwd uit C1 en L1 en een parallelkring samengesteld uit C0 en L1. Het zal duidelijk zijn dat een kristal zich gedraagt zoals iedere andere serie/parallel-schakeling van spoelen en condensatoren. Als u het kristal aansluit op een hoogfrequent generator en de impedantie van het onderdeel meet voor verschillende frequenties, dan ontstaat de karakteristiek van de onderstaande figuur. Bij een bepaalde frequentie fs treedt een minimale impedantie op. Deze frequentie komt overeen met de seriële resonantiefrequentie van het kristal. Bij een iets hogere frequentie fp treedt een maximale impedantie op. Deze frequentie is de parallelle resonantiefrequentie van het onderdeel. De fs wordt bepaald door de serieschakeling van L1 en C1, de fp door het parallel schakelen van C0 aan deze kring.
Let op dat de verticale impedantie-as logaritmisch is ingedeeld en dat er dus een vrij groot verschil bestaat tussen de seriële en parallele resonantie-impedanties van een kristal.|
 |
| Impedantie van een kristal in functie van de frequentie. (© 2022 Jos Verstraten) |
De resonantiefrequenties
Men kan, volgens wiskundige wetten, de exacte waarde van beide resonantiefrequenties berekenen uit de waarden van de onderdelen L1, C0 en C1. Deze formules zijn gegeven in de bovenstaande figuur. Bij de seriële resonantie treedt een fasedraaiing op van nul graden. Dat is een belangrijk gegeven bij het ontwerpen van oscillatorschakelingen! Uit het equivalent schema en de resonantieformules blijkt duidelijk dat u de waarde van de parallel resonantie kunt beïnvloeden door het schakelen van een condensator over het kristal. Dan wordt de waarde van C0 immers aangepast en dit onderdeel bepaalt de fp.
Nu zal er in een praktische schakeling altijd een bepaalde parallelle capaciteit worden geïntroduceerd. Kristallen die worden gespecificeerd door hun parallelle resonantie worden altijd gekalibreerd voor een specifieke waarde van de parallelle externe capaciteit. In de meeste gevallen bedraagt deze extern aan te brengen capaciteit 20 tot 30 pF. De invloed van deze externe capaciteit op de frequentienauwkeurigheid van de oscillator is vrij groot. Een verandering van slechts 0,5 pF op een waarde van 20 pF heeft reeds een frequentiefout van ongeveer 10 parts per million tot gevolg. U kunt dus niet zomaar gelijk welke ceramische condensator parallel schakelen, maar moet zoeken naar onderdelen met minimale temperatuurscoëfficiënt.
De diverse trillingsmodi
Kristallen kunnen zowel op hun seriële als op hun parallelle resonantiefrequentie worden ingesteld. Een en ander is afhankelijk van de schakeling waarin u het onderdeel opneemt. Omdat de frequentie van de parallelle trillingsmodus eenvoudig is te variëren door het parallel schakelen van een condensatortrimmer zal men in de meeste gevallen van deze modus gebruik maken. Kristallen kunnen echter ook op hun harmonische frequenties worden afgestemd. Dat noemt men het 'overtonen' van het kristal. Dat is het rechtstreekse gevolg van de uitgebreide impedantiegrafiek van een kristal, voorgesteld in de onderstaande figuur. In deze grafiek is niet alleen het impedantieverloop weergegeven, maar ook het inductieve of capacitieve gedrag van het kristal. Duidelijk blijkt dat na de punten fs en fp er nog een heleboel frequenties terug te vinden zijn waarbij het kristal een minimale of maximale impedantie heeft. In principe is het mogelijk het kristal op al deze frequenties te laten trillen.
In de praktijk maakt men echter alleen gebruik van de derde en vijfde harmonischen.
 |
| Het volledig impedantieverloop van een kristal. (© 2022 Jos Verstraten) |
'Spurious' frequenties
Na de fp pieken ziet u in de bovenstaande grafiek nog wat kleine impedantie-piekjes. Die piekjes ontstaan bij frequenties die men 'spurious' (onecht) noemt. Hoewel de meeste spurious piekjes enkele tientallen kHz boven de gewenste resonantie liggen, is hun temperatuurscoëfficiënt veel groter dan deze bij de seriële of parallele pieken fs en fp. Dit heeft tot gevolg dat een goed afgestemde kristaloscillator door het verhogen van de kristaltemperatuur opeens kan gaan oscilleren op een van de 'spurious' frequenties en daarin blijft volharden.
De kwaliteitsfactor van een kristal
De amplitude van de trilling over een kristal zal in iedere praktische schakeling afhangen van de kwaliteitsfactor Q van het onderdeel. Deze factor wordt in hoge mate bepaald door de waarde van de R1 uit het equivalent schema.
De kwaliteit van een kristal in parallelle modus wordt gedefinieerd door de zogenaamde 'equivalente parallelle weerstand' EPR. Hoe hoger deze EPR, hoe groter de kwaliteit van het kristal is. Bij serieel bedrijf geldt een waarde ESR, de 'equivalente seriële weerstand'. Nu geldt het omgekeerde, hoe kleiner de ESR, hoe groter de kwaliteit van het kristal. De EPR en ESR zijn waarden die moeilijk te voorspellen zijn bij het zagen van de plaatjes uit het moederkristal. Vaak zal de EPR meer dan een factor vijf verschillen tussen identieke kristaltypen. Alle kristallen van een bepaald type hebben uiteraard wel een minimale EPR en het is deze waarde die u moet aanhouden bij het ontwerpen van schakelingen.
Het gedissipeerde vermogen
Als een kristal wordt toegepast in een oscillator zal er over het onderdeel een bepaalde wisselspanning ontstaan. Deze spanning zal in de EPR of ESR een bepaald vermogen dissiperen. Als er een te grote spanning over het kristal ontstaat zal het gedissipeerde vermogen te groot worden. Dat heeft drie nadelige gevolgen:
- Er kunnen ongewenste oscillaties ontstaan op een van de na fp liggende pieken.
- De dissipatie kan het kristalplaatje opwarmen, waardoor tijdelijke frequentieverschuivingen kunnen optreden.
- Door de grote trillingsamplitude ontstaan mechanische spanningen in het kristal waardoor de resonantiefrequentie blijvend aangetast wordt.
In het algemeen raadt men onderstaande uitsturingsvermogens aan in het kristal:
- 1 MHz tot 3 MHz op grondtoon: 1,0 mW
- 3 MHz tot 20 MHz op grondtoon: 0,5 mW
- Meer dan 20 MHz op grondtoon: 0,2 mW
- 20 MHz tot 140 MHz op harmonischen: 0,5 mW
Temperatuurcompensatie met thermistoren
De frequentie van een kristal is afhankelijk van de temperatuur. Als deze factor niet in de hand is te houden is het verstandig een externe compensatie aan te brengen. In de onderstaande figuur is een schakeling getekend waarmee dit mogelijk is. Bij deze schakeling wordt een varicapdiode parallel geschakeld aan het kristal. Dat kan alleen maar als het kristal met één aansluiting aan de massa zit. Het is immers noodzakelijk de varicap in te stellen in sper en dat kan alleen maar als de massa als referentie kan worden gebruikt. Die instelspanning wordt verzorgd vanuit de positieve stabiele referentiespanning +Uref met behulp van een stel thermistoren ofwel temperatuurgevoelige weerstanden. De thermistoren leveren het stuursignaal voor de varicap, deze past zijn capaciteit zodanig aan dat de kring op een constante frequentie blijft oscilleren.
Uiteraard kunt u deze schakelingen niet zélf ontwerpen, tenzij u een temperatuurkamer en oneindig veel geduld ter beschikking hebt. Diverse fabrikanten leveren echter kant-en-klare temperatuurgecompenseerde kristaloscillatoren in één behuizing, waarbij stabiliteiten tot 1 parts per million realiseerbaar zijn.
 |
| Het principe van de temperatuurcompensatie. (© 2022 Jos Verstraten) |
Oscillatoren met kristallen
Voor een beschrijving van oscillatoren met kristallen wordt verwezen naar een ander artikel op dit blog:
Aanklikbare link ➡ Schakelingen: oscillatoren
Voltcraft LPS1153 labvoeding