Know-how: effectieve waarde RMS

(gepubliceerd op 07-05-2020)

RMS is de Engelse uitdrukking voor de effectieve waarde van een wisselspanning. Deze grootheid biedt één manier waarmee u de grootte van een wisselspanning kunt definiëren.

De effectieve waarde van een wisselspanning

Definiëren van de grootte van een wisselspanning
Alle soorten wisselspanningen hebben één basiseigenschap gemeen. De momentele grootte van de spanning is niet constant, maar afhankelijk van de tijd. Dit wordt, voor een zuiver sinusoidale wisselspanning, toegelicht aan de hand van de onderstaande figuur. Eén periode van de sinusspanning wordt op de horizontale as ingedeeld in 360°. Dit noemt men de 'fasehoek' van de wisselspanning en aan de hand van deze indeling kunt u het verloop van de momentele grootte van de spanning goed definiëren in functie van de periode.
Een tweede manier om de periode van een sinusspanning in te delen en die in de wiskunde wordt toegepast is gebruik te maken van het getal π (Griekse pi). Een volledige periode van de spanning komt overeen met 2 ● π. (Op dit blog wordt het teken ● consequent gebruikt om een vermenigvuldiging aan te duiden. Het normale vermenigvuldigingskruisje wordt op internet meestal voorgesteld door de kleine letter x en kan dus verwarring veroorzaken.)
Nu terug naar de illustratie.
Op tijdstip t0 is de grootte van de spanning gelijk aan 0 V. Nadien gaat de momentele waarde langzaam stijgen tot de maximale waarde Umax, die op moment 0,5 ● π (fasehoek 90°) wordt bereikt. Deze maximale waarde noemt men ook wel de 'amplitude'. Nadien gaat de momentele waarde weer dalen tot de spanning op tijdstip π (fasehoek 180°) weer door de nul gaat. Nadien herhaalt de procedure zich, zij het dat de momentele grootte van de spanning daalt tot een maximale negatieve waarde -Umax op tijdstip 1,5 ● π (fasehoek 270°) en dan weer stijgt tot 0 V op het einde van de periode op tijdstip 2,0 ● π (fasehoek 360°).
Het is uitstekend mogelijk dit verloop wiskundig te formuleren, met de formule:
Ut = Umax ● sin [2 ● π ● f ● t]
waarin:
       - f de frequentie van het signaal is in Hz.
       - t het tijdstip is waarop u de spanning wilt berekenen.
       - Umax de maximale waarde van de spanning is.
       - π het getal pi is, gelijk aan 3,1415.
       - Ut de momentele waarde van de spanning is op tijdstip t.

Het momentele verloop van de grootte van een sinusspanning. (© 2020 Jos Verstraten)

De effectieve waarde RMS
Nu kunt u in de dagelijkse praktijk met die mooie wiskundige formule weinig aanvangen. In de praktijk wilt u de grootte van de spanning als één getal te weten komen, een getal dat u op een meter kunt aflezen en waarmee u bijvoorbeeld het door de spanning opgewekte thermische vermogen in een weerstand kunt berekenen.
Vandaar dat men het begrip 'effectieve waarde' van een wisselspanning heeft ingevoerd. In het Engels wordt het begrip 'Root Mean Square' gebruikt, afgekort tot RMS. De effectieve waarde van een wisselspanning, afgekort tot Ueff of URMS, is gelijk aan de waarde van een gelijkspanning die in een zuiver ohmse weerstand hetzelfde gemiddelde thermische vermogen opwekt als de wisselspanning waarvan men de effectieve waarde definieert.
Dat thermische vermogen is het gevolg van het joule-effect. Het joule-effect, beschreven door de Engelse natuurkundige James Prescott Joule (1818-1889), beschrijft het opwarmen van een weerstand wanneer er elektrische stroom door het onderdeel vloeit. De hoeveelheid thermische energie W die in de weerstand R wordt opgewekt gedurende een tijd t wordt gegeven door de uitdrukking:
W = R ● I² ● t
Uit deze formule kan het gemiddelde thermische vermogen worden afgeleid:
P = (Ueff)² / R
De effectieve waarde kunt u dus niet uit de grafiek van de bovenstaande figuur aflezen. Die Ueff bepaalt echter wél een heleboel eigenschappen van de sinusspanning. In de praktijk zal men sinusspanningen immers steeds aangegeven met hun effectieve waarde. Als men zegt dat de waarde van de netspanning gelijk is aan 230 V, dan bedoelt men te zeggen dat de sinusvormige spanning, die uit de wandcontactdoos komt, in een weerstand hetzelfde gemiddelde warmtevermogen opwekt als een gelijkspanning van 230 V.


Drie spanningsdefinities
Uit de bovenstaande grafiek kunt u drie getallen afleiden die alle drie de grootte van een sinusvormige spanning definiëren:

• Ueff:
  De effectieve waarde.
• Umax:
  De maximale positieve of negatieve waarde van de spanning, ook amplitude genoemd.
• Uttt:
  De top-tot-top waarde van de spanning, ook peak-to-peak genoemd.

Men heeft afgesproken dat men in het dagelijkse gebruik het altijd over de effectieve waarde van een sinusspanning heeft.

Waar komt de naam RMS vandaan?
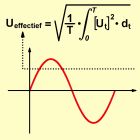
Zoals reeds geschreven staat dit letterwoord voor 'Root Mean Square'. Vertaald kunt u deze terminologie omschrijven als 'de effectieve waarde is gelijk aan de vierkantswortel uit het gemiddelde van het kwadraat van de maximale waarde van de spanning en dit gemeten over één periode van de spanning'. Dat is een nogal ingewikkeld begrip dat uit de theoretische elektriciteitsleer volgt. Wiskundig kan men de effectieve waarde van een wisselspanning namelijk voorstellen door de formule die in de onderstaande figuur is weergegeven. De momentele maximale spanning als functie van de tijd Ut moet achtereenvolgens drie wiskundige bewerkingen ondergaan, namelijk kwadrateren, middelen en worteltrekken, om de RMS-waarde te berekenen.

De wiskundige definitie van de effectieve waarde.
(© 2020 Jos Verstraten)

Het natuurkundig bepalen van de effectieve waarde
Een mooie definitie en een onbegrijpelijke wiskundige formule zijn twee zaken, het omrekenen naar de praktijk van het elektronica-lab een andere! Van een zuivere sinusspanning kunt u maar één gegeven met een oscilloscoop meten en dat is de maximale waarde of amplitude Umax. Hoe moet u nu uit deze meting de effectieve waarde afleiden? Daarvoor heeft men, lang geleden, een mooie meetopstelling verzonnen. Deze is getekend in de onderstaande figuur.
Twee volledig identieke weerstanden R1 en R2 zijn thermisch goed gekoppeld aan twee volledig identieke thermokoppels Th1 en Th2. De twee thermokoppels worden in anti-serie geschakeld en wel zo dat de positieve pool van het ene koppel is verbonden met de positieve pool van het tweede koppel. Deze serieschakeling wordt aangesloten op een zeer gevoelige spanningsmeter M1, een zogenoemde nuldetector. Als u de weerstanden aansluit op spanningen zullen deze onderdelen, als gevolg van het joule-effect, opwarmen. De temperatuur die deze thermische energie veroorzaakt wordt zonder verlies overgedragen van de weerstanden op de thermokoppels. Als beide thermokoppels op dezelfde temperatuur staan wekken zij dezelfde spanning op. Vanwege de anti-serie schakeling zullen deze spanningen van elkaar afgetrokken worden, zodat de meter 0 V aanwijst.
Een van de weerstanden wordt verbonden met de wisselspanning waarvan u de effectieve waarde wilt bepalen. De tweede weerstand wordt via een regelbare weerstand R3 aangesloten op een gelijkspanning Ubat. De twee spanningen veroorzaken stromen door de weerstanden met als gevolg dat deze gaan opwarmen. U moet de gelijkspanning nu zo afregelen dat de nuldetector M1 precies 0 V aanwijst. U weet dan dat beide weerstanden even warm zijn en dat beide spanningen evenveel gemiddeld thermisch vermogen genereren. Met behulp van de spanningsmeter M2 kunt u de waarde van de gelijkspanning meten, die per definitie gelijk is aan de effectieve waarde van de wisselspanning.

De traditionele meetopstelling voor het bepalen van de effectieve waarde van een wisselspanning.
(© 2020 Jos Verstraten)

Het verband tussen amplitude, effectieve waarde en top-tot-top waarde
Als u deze meting uitvoert voor zuiver sinusvormige wisselspanningen stelt u vast dat er een bepaalde verhouding bestaat tussen de amplitude Umax van deze spanning en de gemeten effectieve waarde Ueff. Deze verhouding is:
Ueff = 0,707 ● Umax
Dit is een specifieke eigenschap van zuiver sinusoidale spanningen, die met enige moeite ook wiskundig bewezen kan worden. Iets dat wij op dit blog echter niet gaan doen!
Uit deze formule kunt u natuurlijk ook de amplitude afleiden als u de effectieve waarde kent:
Umax = Ueff / 0,707
of:
Umax = 1,41 ● Ueff
Natuurlijk kunt u nu ook de top-tot-top waarde van een wisselspanning berekenen:
Uttt = 2 ● Umax = 2 ● [1,41 ● Ueff] = 2,82 ● Ueff

De netspanning als voorbeeld
De netspanning met haar effectieve waarde van 230 V heeft dus een amplitude van:
Umax = 1,41 ● 230 V = 324,30 V
De top-tot-top waarde van de netspanning wordt:
Uttt = 2,82 ● 230 V = 648,60 V

Het belang van deze formules
U mag het belang van deze omrekeningsformules voor de praktische elektronica niet onderschatten. Stel dat u een gelijkspanning Udc van 15 V nodig hebt en u deze spanning wilt genereren uit een trafo met gelijkrichter en afvlakelco, zoals getekend in de onderstaande figuur. Hoe groot moet dan de secundaire spanning van de voedingstrafo zijn?
Als u, voor de eenvoud, even geen rekening houdt met spanningsverliezen vanwege stromen door de inwendige weerstanden van de trafo kunt u de bovenstaande formule gebruiken voor het berekenen van de secundaire trafospanning Usec. De afvlakcondensator C1 zal immers worden opgeladen tot de maximale waarde Umax van de secundaire trafospanning minus de spanning over beide geleidende dioden van de brug.
Over een geleidende siliciumdiode valt een spanning van 0,65 V. U moet 2 ● 0,65 V optellen bij de gelijkspanning die de trafo moet genereren.
De trafo moet dus een gelijkspanning genereren van:
15,0 V + 1,3 V = 16,3 V
Uit deze wetenschap kunt u de effectieve waarde van de secundaire wikkeling van de trafo berekenen:
Usec = 0,707 ● Umax
Usec = 0,707 ● 16,3 V
Usec = 11,52 V
Let wel dat dit een benadering geeft! Als u de gelijkspanning gaat belasten gaat er een stroom door de wikkelingen van de trafo vloeien. Deze wikkelingen hebben een bepaalde weerstand en het gevolg is dat er over deze weerstanden kleine spanningen vallen. Als de trafo dus onbelast 11,52 V levert, dan zal deze spanning dalen als u stroom gaat trekken.
Bovendien zal ook de gelijkspanning over de condensator meer rimpel gaan vertonen bij belasting, waardoor de gemiddelde spanning over dit onderdeel daalt.
Met deze rekenmethode kunt u dus alleen de absoluut minimale secundaire trafospanning berekenen die u nodig hebt om een bepaalde gelijkspanning te genereren.

Het belang van de 0,707 factor bij gelijkrichting van een wisselspanning. (© 2020 Jos Verstraten)

Het begrip crest-factor Cr

Wat is de crest-factor?
De verhoudingsfactor van 1,41 tussen de effectieve waarde en de maximale waarde van een wisselspanning geldt uitsluitend voor volledig zuivere sinusoidale spanningen. Alle andere spanningsvormen hebben een andere verhouding.
De crest-factor Cr geeft de verhouding tussen de maximale waarde van een wisselspanning en de effectieve waarde van deze spanning. In formulevorm:
Cr = Umax / Ueff
Voor een zuivere sinus is Cr dus gelijk aan 1,414.
Immers:
Umax = 1,41 ● Ueff
Cr = [1,41 ● Ueff] / Ueff = 1,41
Voor andersvormige wisselspanningen kan de crest-factor echter nogal afwijken van deze waarde:
       - Driehoekspanning: Cr = 1,732
       - Zaagtandspanning: Cr = 1,732
       - Symmetrische blokspanning: Cr = 1

De crest-factor bij PWM-signalen
Tegenwoordig worden heel wat gelijkspanningsbelastingen, zoals LED-lampen en DC-motoren, in vermogen geregeld door middel van een in pulsbreedte gemoduleerd signaal. Dat wordt PWM genoemd, letterwoord van 'Pulse Width Modulation' of 'pulsbreedte modulatie'. Door de duty-cycle, dus de AAN/UIT-verhouding van een pulsvormige spanning, te variëren kunt u het vermogen dat u aan de belasting toevoert op een heel efficiënte manier regelen. Het is dan van belang een relatie te leggen tussen de duty-cycle van de puls en het geleverde vermogen. Het zal duidelijk zijn dat ook hier de effectieve waarde van het signaal van pas komt. Deze waarde kunt u echter niet meten omdat de standaard multimeters helemaal niet in staat zijn de effectieve waarde van zo'n pulsspanning te meten.
Wat echter wél kan is een verband leggen tussen de AAN/UIT-verhouding (duty-cycle) van de puls en de crest-factor. Dit verband is voorgesteld in de onderstaande figuur. U kunt de duty-cycle van het signaal gemakkelijk meten met de oscilloscoop. Met de gegeven formule kunt u de crest-factor bepalen met ieder rekenmachine dat het berekenen van een vierkantswortel mogelijk maakt.
De effectieve waarde van de PWM-spanning kunt u dan berekenen door de maximale waarde van de puls (de amplitude) te delen door de crest-factor.

De waarde van de crest-factor bij PWM-signalen. (© 2020 Jos Verstraten)

Een voorbeeld
Stel dat uw PWM-systeem werkt met pulsen met een frequentie van 1 kHz. De periodetijd t1 is dan gelijk aan 1 ms. Stel dat u de duty-cycle instelt op 10 %. De tijd t2 is dan gelijk aan 0,1 ms. De crest-factor wordt berekend als de vierkantswortel uit de verhouding 1 / 0,1 of de vierkantswortel uit 10. Uw rekenmachine beweert dat dit gelijk is aan 3,162.
Stel dat de amplitude van de pulsen gelijk is aan 10 V. De effectieve waarde van dit signaal is dan gelijk aan:
Ueff = 10 V / 3,162 = 3,15 V
Stel dat de belasting bestaat uit een weerstand van 10 Ω. Als u de volle 10 V aan deze belasting aanlegt, dan is het gemiddelde thermische vermogen:
P = (Ueff)² / R = [10 ● 10] / 10 = 10 W
Bij een gelijkspanning is er immers geen verschil tussen de maximale en de effectieve waarde.
Als u de duty-cycle instelt op 10 %, dan wordt het gemiddelde thermische vermogen:
P = (Ueff)² / R = [3,15 ● 3,15] / 10 = 0,99 W



De crest-factor bij fase-aansnij signalen
Hetzelfde probleem doet zich voor als u met triac-schakelingen het vermogen regelt dat u aan wisselspanningbelastingen toevoert. U werkt dan met fase-aansnijding, waarbij u maar een deel van de halve perioden van het sinussignaal doorlaat naar de belasting. Dat deel wordt bepaald door de grootte van de ontstekingshoek. Als deze hoek gelijk is aan 0° wordt de volledige halve periode van het signaal aangeboden aan de belasting. Als deze hoek gelijk is aan 180° wordt de volledige halve periode gesperd en krijgt de belasting geen voeding. Het is van belang een relatie te leggen tussen de grootte van de ontstekingshoek en het vermogen dat in de belasting wordt gegenereerd. Ook nu moet u werken via de omweg van de crest-factor. In de onderstaande figuur is het verband tussen de ontstekingshoek en de crest-factor grafisch voorgesteld.
Als de hoek gelijk is aan 0° is de crest-factor gelijk aan 1,414. Geen wonder, want dan worden de volledige halve perioden doorgelaten naar de belasting en staat er dus een zuivere sinusspanning over de belasting. Naarmate de ontstekingshoek groter wordt zal ook de crest-factor groter worden. Als de hoek de waarde van 180° nadert zal de crest-factor heel snel stijgen om oneindig te worden bij 180°.

De waarde van de crest-factor bij fase-aansnij signalen. (© 2020 Jos Verstraten)

Een voorbeeld
Stel dat u uw dimmer instelt op een ontstekingshoek van 150°. Dat kunt u met uw oscilloscoop meten. Uit de bovenstaande grafiek kunt u aflezen dat de crest-factor dan gelijk is aan 4,0.
Stel dat de amplitude van de wisselspanning gelijk is aan 324,30 V (de netspanning). De effectieve waarde van dit signaal is dan gelijk aan:
Ueff = 324,30 V / 4,0 = 81,07 V
Stel dat de belasting bestaat uit een weerstand van 100 Ω. Als u de volle 230 Veff van de netspanning aan deze belasting aanlegt dan is het gemiddelde thermische vermogen:
P = (Ueff)² / R = [230 ● 230] / 100 = 529 W
Als u de ontstekingshoek instelt op 150° wordt het gemiddelde thermische vermogen:
P = (Ueff)² / R = [81,07 ● 81,07] / 10 = 65,72 W

De effectieve waarde nauwkeurig meten

Inleiding
Om nauwkeurig te kunnen berekenen hoeveel thermisch vermogen een wisselspanning opwekt in een resistieve belasting is het noodzakelijk de effectieve waarde van de spanning te kennen.
Het komt er dus op neer een nauwkeurige meetmethode te vinden. De beschreven thermische meetopstelling is uiterst nauwkeurig maar is in de praktijk uiteraard nogal onpraktisch. U wilt een meter ter beschikking hebben, waarop u de effectieve waarde van een wisselspanning onmiddellijk kunt aflezen.
Als u in de praktijk alleen zuiver sinusoidale wisselspanningen meet, is dit geen probleem. Het volstaat immers de meter eenmalig te ijken met behulp van de beschreven verhouding tussen maximale en effectieve waarde. Vanaf dat moment zal de meter de effectieve waarde van sinusspanningen nauwkeurig aangegeven.
Meet u echter met een multimeter de wisselspanning die een dimmer levert die werkt volgens het systeem van fase-aansnijding of -afsnijding, dan zal de meter een foutieve spanningswaarde aangeven. U kunt dan met geen mogelijkheid het vermogen berekenen dat deze is fase aangesneden wisselspanning aan bijvoorbeeld een verwarmingselement levert. Daarvoor hebt u immers de effectieve waarde van de wisselspanning nodig.

True RMS multimeters
Gelukkig zijn de meeste moderne digitale multimeters in staat de echte effectieve waarde van een wisselspanning te berekenen. Deze meters worden 'True RMS' genoemd. Echter, aan de nauwkeurigheid van deze meting zit een grens. Deze wordt bepaald door de crest-factor van de wisselspanning. Iedere goede meter die true RMS meet heeft in de specificaties een tabelletje staan waaruit u kunt afleiden welke extra meetfout een van 1,414 afwijkende crest-factor tot gevolg heeft.
Bij dergelijke moderne microcontroller bestuurde multimeters worden digitale principes gebruikt. Het wisselspanningssignaal wordt op een zo hoog mogelijke frequentie bemonsterd om de golfvorm zo goed mogelijk vast te leggen. De RMS-waarde wordt dan berekend met behulp van de vierkantswortel van de gemiddelde waarde van de kwadraten van de afzonderlijke metingen.
U moet er echter wél rekening mee houden dat er grenzen zijn aan de crest-factor waarbij multimeters nog een betrouwbare indicatie geven.

Digitale oscilloscopen
De meeste digitale oscilloscopen kunnen op een identieke manier de RMS-waarde van de opgenomen golfvorm direct weergeven op hun scherm. Maar ook bij deze instrumenten geldt dat er een grens zit aan de crest-factor waarbij u op de metingen kunt vertrouwen.

True RMS-to-DC converters
IC-fabrikant Analog Devices heeft een aantal lineaire IC's ontwikkeld, waarmee u zélf de echte effectieve waarde van een wisselspanning kunt meten. Dergelijke lineaire schakelingen gaan door het leven onder de naam 'true RMS-to-DC converters'. Zoals deze naam reeds doet vermoeden zetten deze de wisselspanning op de ingang om in een gelijkspanning die dezelfde waarde heeft als de effectieve waarde van de ingangsspanning. Deze gelijkspanning kunt u dan digitaal of analoog meten. Deze schakelingen leveren ook bij grote crest-factoren een nauwkeurige berekening van de echte effectieve waarde van het ingangssignaal..
Om u een voorbeeld te geven van de nauwkeurigheid van dergelijke schakelingen ziet u in de onderstaande grafiek de nauwkeurigheid van de uitgangsspanning van de AD536A van Analog Devices. Zelfs bij een crest-factor van 10 zal de fout op de RMS-naar-DC omzetting maar 2,5 % bedragen. Dat is een waarde waar u bij een digitale multimeter of oscilloscoop alleen maar van kunt dromen!

De nauwkeurigheid van een AD536A in functie van de crest-factor.
(© 2020 Jos Verstraten)

De thermische omzetter LT1088
Tot slot bespreken wij nog in het kort een bijzonder IC van Linear Technology. De LT1088, die niet minder dan € 50,00 kost, gebruikt het in de inleiding van dit artikel beschreven thermische principe om de echte effectieve waarde van een wisselspanning te bepalen. In de chip zijn twee even grote precisieweerstanden en twee gepaarde dioden aangebracht. Iedere weerstand is thermisch gekoppeld aan een diode. De vier onderdelen zijn ondergebracht in een ruimte in de chip die thermisch afgesloten is van de omgeving.
U snapt het al: over een van de weerstanden legt u de wisselspanning aan waarvan u de effectieve waarde wilt meten, over de andere weerstand legt u een instelbare gelijkspanning. U ontwerpt een teruggekoppeld systeem dat het verschil tussen de twee diodespanningen meet en de gelijkspanning zó regelt dat dit verschil nul is. Op dat moment is de gelijkspanning over de ene weerstand gelijk aan de effectieve waarde van de wisselspanning over de tweede weerstand.
Dit systeem heeft een maximale fout van 1 % tot 10 MHz en een crest-factor tot 50!

Het nauwkeurig bepalen van de effectieve waarde met een LT1088 als basis. (© Linear Technology)

Gemiddelde waarde Ugem van een wisselspanning

Iets anders dan de effectieve waarde
Tot slot van dit artikel bespreken wij nog even het begrip 'gemiddelde waarde'. Leken willen deze waarde wel eens verwarren met de effectieve waarde. Toch zijn beide grootheden alles behalve identiek! Zo kunt u de gemiddelde waarde van een sinusspanning nooit bepalen over een volledige periode. De gemiddelde waarde van de sinusspanning, gemeten over een volledige periode, is namelijk gelijk aan nul.
Vandaar dat u deze parameter alleen kunt bepalen voor de halve periode van de spanning. In de onderstaande figuur is voorgesteld hoe dat werkt. De rode curve die het verloop van de spanning over een halve periode t1 definieert omsluit een bepaald oppervlakte S1. Dit oppervlakte is in de figuur rose weergegeven. U kunt nu op dezelfde schaal een rechthoek tekenen met een breedte t2 die gelijk is aan de halve periode t1 en waarvan het oppervlakte S2 gelijk is aan het oppervlakte S1 dat door de halve sinus wordt omsloten. De hoogte Ugem van deze rechthoek op de verticale as is gelijk aan de gemiddelde waarde van de sinusspanning.

De grafische voorstelling van de gemiddelde waarde.
(© 2020 Jos Verstraten)

De omrekeningsformule voor de gemiddelde waarde
Het verband tussen de maximale waarde Umax en de gemiddelde waarde Ugem van een zuivere sinusspanning wordt gegevens door de uitdrukking:
Ugem = 0,630 ● Umax



(Amazon sponsor advertentie)
Koop uw Current-clamp meter bij Amazon