Achtergrondinformatie
Van mechanische naar elektronische klokken
Toen de digitale elektronica begon door te breken bedacht men dat een belangrijke toepassing van deze technologie tijdmeting kon zijn. Mechanische klokken hadden immers grenzen wat betreft nauwkeurigheid en moesten regelmatig gelijk worden gezet met de standaard tijd. Daarvoor bestond zelfs een speciaal telefoonnummer waarmee iedereen alle klokken in huis gelijk kon zetten.
Omdat alle mechanische klokken werkten met een één seconde tik was men op zoek naar een mogelijkheid om zo'n één seconde tik elektronisch te genereren. Zeer nauwkeurige kwartskristallen waren bekend, maar resoneerden op frequenties van minstens honderden kHz. Om uit zo'n signaal een tik met een periode van exact één seconde af te leiden vergde een heleboel digitale elektronica.
Zo ontstond de behoefte aan een kristal dat op een veel lagere frequentie kon resoneren en werd het stemvork kristal uitgevonden dat werkt op een frequentie van slechts een paar tientallen kHz.
Snelle ontwikkeling in de jaren zeventig van de vorige eeuw
Al in 1927 presenteerden de Amerikanen 's werelds eerste kwartsgestuurde digitale klok. Er gingen echter tientallen jaren voorbij voordat het 'quartzhorloge' zoals het werd genoemd de weg naar de massamarkt vond. In 1969 bracht het Japanse bedrijf Seiko het eerste commercieel verkrijgbare polshorloge met kristal op de markt. De prijs van 460.000 yen was echter vergelijkbaar met die van een kleine auto. Maar de ontwikkeling ging snel. Halverwege de jaren zeventig waren quartzhorloges al goedkoper dan de horloges met puur mechanische uurwerken.
Waarom 32,768 kHz?
De meeste stemvork kristallen die u in de handel aantreft hebben een frequentie van exact 32,768 kHz. Dat heeft bepaalde redenen. Op de eerste plaats blijkt dat men, door een kwartskristal op een bepaalde manier te snijden, op een goedkope manier een kwartsschijfje kan maken dat op een dergelijke frequentie resoneert. Op de tweede plaats kan men uit deze frequentie door middel van een aantal standaard flip-flop's een signaal met een frequentie van exact 1 Hz afleiden. Zoals u ongetwijfeld weet kunt u met een flip-flop de frequentie van een blokvormig signaal exact door twee delen. Telt u maar even mee waar wij uitkomen als wij uitgaan van een signaal met een frequentie van 32,768 kHz:
- uitgang flip-flop 1: 16,384 kHz
- uitgang flip-flop 2: 8,192 kHz
- uitgang flip-flop 3: 4,096 kHz
- uitgang flip-flop 4: 2,048 kHz
- uitgang flip-flop 5: 1,024 kHz
- uitgang flip-flop 6: 512 Hz
- uitgang flip-flop 7: 256 Hz
- uitgang flip-flop 8: 128 Hz
- uitgang flip-flop 9: 64 Hz
- uitgang flip-flop 10: 32 Hz
- uitgang flip-flop 11: 16 Hz
- uitgang flip-flop 12: 8 Hz
- uitgang flip-flop 13: 4 Hz
- uitgang flip-flop 14: 2 Hz
- uitgang flip-flop 15: 1 Hz
U hebt dus 15 identieke en eenvoudige flip-flop schakelingen nodig om een puls met een frequentie van exact één seconde uit het stemvork kristal af te leiden.
De nauwkeurigheid
De gemiddelde nauwkeurigheid van een door een stemvork kristal aangedreven horloge is driehonderd keer beter dan deze van een horloge met een mechanische resonator. Het is technologisch geen enkel probleem om stemvork kristallen te maken met een frequentie-afwijking van slechts ±20 ppm (parts per million).
De fundamentele werking van een stemvork kristal oscillator
Een stemvork kristaloscillator werkt zoals iedere andere kristaloscillator. Bepaalde natuurlijke materialen zoals kwarts vertonen een piëzo-elektrisch effect. Wanneer een plaatje van zo'n materiaal wordt samengedrukt of uitgerekt ontstaat er over het materiaal een elektrische spanning. Als u een elektrische spanning over het materiaal zet dan zal dit samengedrukt of uitgerekt worden. Het materiaal reageert dus op een wisselend elektrisch veld door het uitvoeren van een periodieke beweging. De frequentie waarmee dit gebeurt is afhankelijk van de fysische eigenschappen van het materiaal, met name de vorm en de dikte van het plaatje.
Door deze eigenschap is het mogelijk een materiaal met piëzo-elektrische eigenschappen te gebruiken voor het genereren van een wisselspanning met een zeer constante frequentie. Als u over een plaatje materiaal met dergelijke eigenschappen een breedbandige ruisspanning zet, dan zal het plaatje één frequentie uit dit signaal gaan versterken. Dat is de frequentie waarop het plaatje maximaal gaat trillen. Door dit trillen en door het genoemde effect zal er over het plaatje namelijk een vrij grote spanning ontstaan waarvan de frequentie gelijk is aan de resonantiefrequentie van het plaatje.
De eigenschappen van een stemvork kristal
De snede (cut)
Uit een basiskristal, zie onderstaande foto, kunnen duizenden dunne plaatjes worden gezaagd. Deze plaatjes vormen de basis van de elektronische onderdelen die men kristallen noemt.
 |
| Het basiskristal waaruit de stemvork kristallen worden gesneden. (© 2009 Nakagawa Electronics) |
De eigenschappen van het plaatje hangen niet alleen af van de dikte, maar ook van de hoek (de 'snede' of 'cut') waaronder de plaatjes uit het basiskristal worden gezaagd. Er zijn in de loop der tijd tientallen snedes uitgeprobeerd die ieder iets andere specificaties aan het kristal geven. Dat gaat dan voornamelijk over de verouderingsverschijnselen, de thermische stabiliteit en de frequentie stabiliteit. De dikte en de vorm van het plaatje bepalen de uiteindelijke resonantiefrequentie van het kristal, de snede is verantwoordelijk voor de mate waarin de resonantiefrequentie afhankelijk is van de temperatuur.
Voor stemvork kristallen wordt gebruik gemaakt van de X-snede (lichtblauw in de onderstaande illustratie). Deze snede werd door Walter Guyton Cady toegepast in een van de eerste elektronische kristalklokken, in 1927 ontworpen door Henry Bishop Horton en Warren Marrison.
 |
| Diverse snedes door een kwarts kristal. (© 2024 Jos Verstraten) |
De vorm van het kristalplaatje
Stemvork kristallen ontlenen hun specifieke eigenschappen, zoals de zeer lage resonantiefrequentie, aan hun specifieke vorm. Deze onderdelen heten uiteraard niet voor niets 'stemvork' kristallen. De vorm van het plaatje is inderdaad volledig te vergelijken met de vorm van de bekende metalen stemvorken, die worden gebruikt voor het stemmen van muziekinstrumenten en die, volgens sommige gelovigen, ook allerlei heilzame werkingen hebben op lichaam en geest.
In de onderstaande foto ziet u de typische vorm van zo'n plaatje, nu helaas al voorzien van opgedampte elektroden en gemonteerd in een behuizing. Een foto van een 'naakt' stemvork kristalletje konden wij niet vonden.
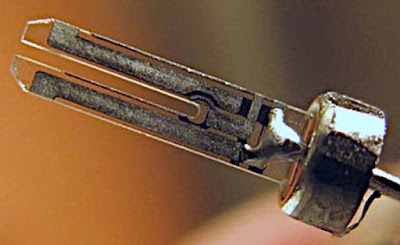 |
| De typische vorm van een stemvork kristal. (© Wikimedia Commons) |
De trillingsmodus van stemvork kristallen
Een kristalplaatje kan op diverse manieren trillen, dit noemt men de 'modi' van het kristal. Een stemvork kristal trilt volgens de zogenaamde 'flexure mode'. Dat is voorgesteld in de onderstaande figuur. Als tussen de twee tanden van de stemvork een wisselspanning wordt aangelegd gaan de twee tanden vervormen, waardoor de afstand tussen de tanden groter en kleiner wordt. Net zoals bij een metalen stemvork wordt de frequentie van die trilling bepaald door de afmetingen van de stemvork en de dikte van het plaatje.
 |
| De flexure trillingsmodus. (© 2009 Nakagawa Electronics) |
Het aanbrengen van de elektroden
Zoals uit een van de vorige foto's blijkt volstaat het niet twee eenvoudige elektroden op een van de zijden van het kristal op te dampen. Dat heeft te maken met het feit dat het absoluut noodzakelijk is alle acht zijden van de twee tanden van de vork te voorzien van elektrische polarisatie. In de onderstaande figuur ziet u een bovenaanzicht van de twee tanden van de stemvork en de elektrische polarisatie die noodzakelijk is om de vork aan het trillen te krijgen.
 |
| Bovenaanzicht van de tanden van de stemvork. (© 2009 Nakagawa Electronics) |
Om dat voor elkaar te krijgen met slechts één laag opgedampt aluminium of zilver per zijde moet een vrij ingewikkeld elektrodenpatroon worden aangebracht. In de onderstaande figuur ziet u bijvoorbeeld hoe men dat bij de fabrikant Nakagawa Electronics uit Hong Kong oplost.
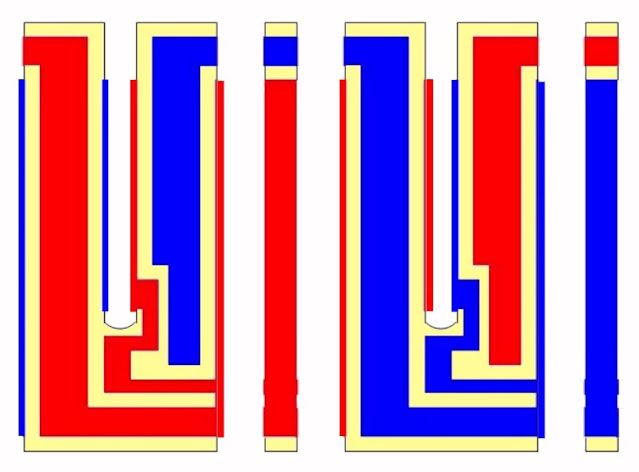 |
| Voor-, achter- en zijaanzichten van de opgedampte tanden van de stemvork. (© 2009 Nakagawa Electronics) |
Inbouwen in de behuizing
Stemvork kristallen kunt u kopen in allerlei uitvoeringen, zowel als component met draadjes ('through hole') als in een SMD-vorm. In de onderstaande foto ziet u enige uitvoeringsvormen van deze handige en goedkope onderdelen.
 |
| Diverse uitvoeringsvormen van stemvork kristallen, niet op schaal. (© 2024 Jos Verstraten) |
Dank zij de tweezijdige opdamping is het mogelijk het kristalplaatje tussen twee elektroden te klemmen en op deze elektroden vast te solderen. In de onderstaande tekening ziet u hoe dat gebeurt bij een through hole uitvoering.
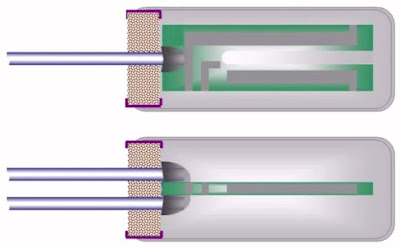 |
| Montage van het plaatje in een through hole behuizing. (© 2009 Nakagawa Electronics) |
Het equivalent schema van een stemvork kristal
Wat deze eigenschap betreft gedragen stemvork kristallen zich net zoals hun hoogfrequente broeders en zusters. Het equivalent schema is een serie/parallel-schakeling van weerstanden, condensatoren en spoelen die de elektrische eigenschappen van het onderdeel precies nabootst. Het equivalent schema en het symbool van een stemvork kristal zijn getekend in de onderstaande figuur. De vier elementen vertegenwoordigen:
- L1: de resonerende massa van het kristalplaatje
- C1: de elastische compliantie van het plaatje
- R1: de wrijvingsverliezen tijdens het oscilleren
- C0: de capaciteit van het kristalplaatje en de capaciteit van de behuizing.
 |
| Het equivalent schema van een stemvork kristal. (© 2024 Jos Verstraten) |
Verouderen van een stemvork kristal
De karakteristieken van een stemvork kristal veranderen iets naarmate het onderdeel ouder wordt. Een van de belangrijkste oorzaken is het migreren van verontreinigingen van de behuizing naar het kristalplaatje. Daarnaast zal er ook migratie plaats vinden van het oppervlak van het plaatje naar de behuizing, waardoor het plaatje dus iets dunner wordt. Tot slot zullen de trillingskarakteristieken van het plaatje langzaam veranderen. Het lijkt alsof het plaatje stijver wordt naarmate het langer trilt. Als u al deze effecten bij elkaar optelt komt u uit op een gemiddeld verouderingseffect van ongeveer 5 ppm/y (parts per million per jaar). Zoals uit de onderstaande grafiek blijkt is het verouderingseffect het sterkst in de eerste levensmaanden van het kristal. Vandaar dat er stemvork kristallen te koop zijn die een 'pre-aging' cyclus hebben doorlopen. Dergelijke kristallen worden, na de fabricage, kunstmatig verouderd zodat de snelle afwijking in het begin van de levensloop van het onderdeel wordt overgeslagen en u daar als gebruiker geen last van hebt.
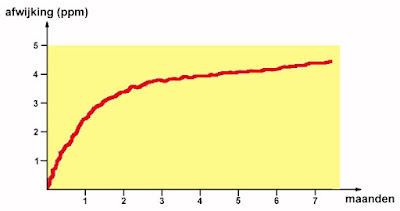 |
| Het verouderen van een stemvork kristal. (© 2024 Jos Verstraten) |
De temperatuurscoëfficiënt
De afwijking op de resonantiefrequentie onder invloed van de omgevingstemperatuur wordt altijd gespecificeerd ten opzichte van de resonantiefrequentie bij +25 °C. Zoals uit de onderstaande grafiek blijkt verloopt de afwijking volledig symmetrisch onder de vorm van een inverse paraboolfunctie bij dalende of stijgende temperaturen.
Om de een of andere reden wordt de tempco uitgedrukt in ppm/°C². Deze grootheid wordt de 'parabolische coëfficiënt B' of de 'curvature constant' genoemd.
 |
| De temperatuurscoëfficiënt van een stemvork kristal. (© 2024 Jos Verstraten) |
De frequentie
Zoals reeds geschreven hebben de meeste in de handel verkrijgbare stemvork kristallen een frequentie van 32,768 kHz. De technologie laat echter zonder problemen toe kristallen te fabriceren met een frequentie tussen 30 kHz en 200 kHz.
De vermogensopname
Stemvork kristallen hebben extreem weinig vermogen nodig om te oscilleren. Het gemiddeld vermogensverbruik ligt rond 1 μW! Let wel dat dit het opgenomen vermogen van het kristal zélf is en niet dat van de schakeling waarin het kristal aanwezig is.
De schokbestendigheid ('shock resistance')
Als u een stemvork kristal laat vallen zal de frequentie iets afwijken. Deze schokbestendigheid wordt meestal gemeten door het onderdeel drie keer van een hoogte van 75 cm te laten vallen op een ondergrond van hard hout. De frequentie-afwijking die hiervan het gevolg is bedraagt gemiddeld ±5 ppm. Dat lijkt niet veel, maar als u bedenkt dat u stemvork kristallen kunt kopen met een nauwkeurigheid binnen ±20 ppm betekent dat toch een behoorlijk grote aantasting van de gespecificeerde nauwkeurigheid.
Verkrijgbare types
Inleiding
Er zijn tientallen, misschien wel honderden stemvork kristallen van 32,768 kHz geproduceerd. In de onderstaande paragraafjes beschrijven wij in het kort een paar types die goedkoop zijn en bovendien ook nog leverbaar.
YXC2060 van Shenzhen Yangxing Technology
Voer op de site van AliExpress de zoekterm '32.768 kHz crystal' in en u krijgt een heleboel referenties. In de 'NUOWIIN Official Store' wordt bijvoorbeeld een partij van tien stuks aangeboden voor, inclusief verzending, iets meer dan twee euro! Dergelijke onderdelen zijn vaak volledig naamloos en worden zonder veel specificaties geleverd. Nader onderzoek leert ons dat deze aanbiedingen in de meeste gevallen gaan over de YXC2060 van Shenzhen Yangxing Technology. Veel gegevens over dit onderdeel kunnen wij echter niet vinden.
 |
| De YXC2060 van Shenzhen Yangxing Technology. (© 2024 Jos Verstraten) |
MH32768 van Euroquart
Als u meer vertrouwen hebt in onderdelen die niet anoniem zijn zou u bijvoorbeeld dit type van het Engelse Euroquartz kunnen aanschaffen. Het ziet er precies hetzelfde uit als de naamloze modellen uit China, is 6,2 mm lang en heeft een diameter van 2,0 mm. Het wordt door Farnell verkocht voor € 0,315 per stuk. Afhankelijk van de suffix bedraagt de nauwkeurigheid ±5 ppm tot ±50 ppm.
De overige specificaties:
- Temperatuur coëfficiënt: -0,035 ppm/°C²
- Shunt capaciteit C1: 0,8 pF typisch
- Serieweerstand R1: 45 kΩ max.
- Serie capaciteit Co: 4,0 pF max.
- Temperatuurbereik: -55 °C ~ +105 °C
- Veroudering: ±5 ppm/y
- Shock resistance: ±5 ppm max.
Dit stemvork kristal zit, zie de onderstaande figuur, in een eigenzinnige vormgeving met een totale lengte van 8 mm en een dikte van 1,78 mm. Dit model wordt te koop aangeboden onder diverse merknamen, maar wij nemen aan dat Statek de échte fabrikant is.
- Nauwkeurigheid: ±30 ppm tot ±200 ppm
- Temperatuur coëfficiënt: -0,035 ppm/°C²
- Veroudering: ±5 ppm/y
- Shunt capaciteit C1: 2,0 pF typisch
 |
| De CX1V van Statek. (© Statek) |
MC306 van Seiko Epson Corporation
Met zijn afmetingen van 8,0 mm × 3,8 mm × 2,54 mm is dit stemvork kristal is geschikt voor SMD-montage. Intern is het kristal verbonden met de twee linker aansluitingen van de behuizing. U betaalt er € 1,96 per stuk voor.
De voornaamste specificaties:
- Nauwkeurigheid: ±20 ppm tot ±100 ppm
- Temperatuurbereik: -40 °C ~ +85 °C
- Temperatuur coëfficiënt: -0,04 ppm/°C²
- Shunt capaciteit C1: 0,6 pF typisch
- Serieweerstand R1: 50 kΩ max.
- Serie capaciteit Co: 0,6 pF max.
- Veroudering: ±5 ppm/y
 |
| De MC306 van Seiko Epson Corporation. (© Epson) |
32,768 kHz oscillator JRO32
Naast losse stemvork kristallen kunt u ook complete 32,768 kHz oscillatoren in SMD-uitvoering aanschaffen. Een van de bekendste typen is de JRO32 die door diverse fabrikanten wordt aangeboden, onder andere door Jauch. Er bestaan ook diverse Chinese look-alikes van dit type. U betaalt er ongeveer € 1,70 voor. De oscillator zit in een SMD-behuizing van 3,2 mm x 2,5 mm en heeft vier aansluitingen:
- Massa
- Voedingsspanning
- Uitgang
- Standby besturing
De voornaamste specificaties:
- Voedingsspanning: +1,5 V ~ +5,0 V
- Voedingsstroom: 2,5 μA (5,0 V) ~ 1,5 μA (3,3 V)
- Nauwkeurigheid bij 25 °C: ±20 ppm
- Frequentie afwijking tussen -20 °C en +70 °C: -90 ppm ~ +10 ppm
- Uitgangssignaal: rechthoekspanning
- 'L'-niveau: 0,4 V max.
- 'H'-niveau: voeding - 0,4 V min.
- Capacitieve belasting: 15 pF max.
- Stijg- en daaltijd: 200 ns max.
- Uitgangsstroom actief: 400 µA max.
- Uitgangsstroom standby: 1 µA max.
 |
| De complete 32,768 kHz oscillator JRO32. (© Jauch) |
Schakelingen met stemvork kristallen
De algemene oscillatie-voorwaarden
Uiteraard moeten ook oscillatoren met stemvork kristallen voldoen aan de twee algemene oscillatie-voorwaarden:
- De amplitude voorwaarde
De oscillatie ontstaat en zal in stand blijven, dan en slechts dan als de rondgaande versterking minstens gelijk is aan 1. In formulevorm: K • A ≥ 1. K is de koppelfactor, A de versterking van de schakeling. Als K kleiner is dan A-1, dan zal de schakeling na het aanzetten niet gaan oscilleren. Als u de schakeling door een externe impuls toch in oscillatie brengt zal het signaal op de uitgang langzaam maar zeker uitsterven. - De fase voorwaarde
Een deel van de uitgangsspanning moet in fase op de ingang van de schakeling verschijnen. Onder de vorm van een formule: φ = 0°.
Wij bespreken een aantal schakelingen die aan deze voorwaarden voldoet.
Een eenvoudige een-transistor schakeling
In de onderstaande figuur is het schema gegeven van een Colpitts-oscillator met één transistor en met een stemvork kristal in de terugkoppeling. Bij een snelle blik op deze schakeling lijkt deze niet te kunnen werken. Immers, de transistor is geschakeld als emittervolger en heeft dus een versterking die iets kleiner is dan een. Hoe wordt dan aan de eerste oscillatie-voorwaarde voldaan? Bedenk echter dat een kristal, onder de juiste voorwaarden, een wisselspanning met de eigen resonantiefrequentie kan opslingeren, waardoor toch voldoende signaal wordt teruggekoppeld om de oscillatie in stand te houden. Op de uitgang verschijnt een nogal vervormd sinussignaal waarmee u niet rechtstreeks digitale frequentiedelers kunt aansturen.
 |
| Een een-transistor oscillator. (© 2024 Jos Verstraten) |
Een drie-transistor oscillator
U kunt een stemvork resonator volgens de onderstaande figuur opnemen in een traditionele oscillator schakeling. Twee transistoren T1 en T2 zijn in cascade geschakeld. De stemvork zit in een terugkoppel circuit tussen de uitgang van de tweede versterkertrap en de basis van de eerste transistor. Door de hoge versterkingsfactoren van de twee transistoren zal oscilleren zelfs optreden bij een kristal met een hoge impedantie. Door de grote spanningsversterking van de transistoren en het faseverschil tussen in- en uitgangsignaal van 360° zal een kleine strooicapaciteit al voldoende zijn om de schakeling te laten oscilleren. Om oversturing van het stemvork kristal te voorkomen moet u de initiële stroom begrenzen op 1 μA. Dit kunt u bereiken door de spanning over het kristal te begrenzen op 1,5 V. Om toch een hogere voedingsspanning toe te kunnen passen is de spanningsdeler R4/R5 noodzakelijk.
De derde transistor zorgt voor een blokvormige uitgangsspanning met voldoende stijgtijd om zowel CMOS als TTL-schakelingen zonder problemen te kunnen aansturen.
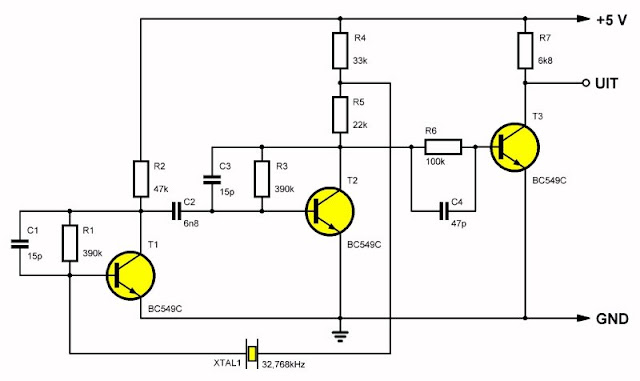 |
Een drie-transistor oscillator. (© 2024 Jos Verstraten) |
Oscillatoren met inverters
Zowel in TTL als in CMOS zijn IC's beschikbaar die een aantal inverters bevatten. Deze schakelingen zijn ideaal voor het opbouwen van een mooie en simpele 32,768 kHz oscillator. In de onderstaande figuur is bijvoorbeeld een zeer eenvoudige oscillator getekend rond twee poorten uit een 74HC04. De eerste poort vormt de eigenlijke oscillator, de tweede poort buffert het signaal en maakt er een snelle puls van waarmee u rechtstreeks de delerketen kunt aansturen.
 |
| Oscillator met 74HC04 poorten. (© 2024 Jos Verstraten) |
In de onderstaande figuur ziet u een identieke schakeling, maar dan opgebouwd rond de poorten uit een CD4069 inverter.
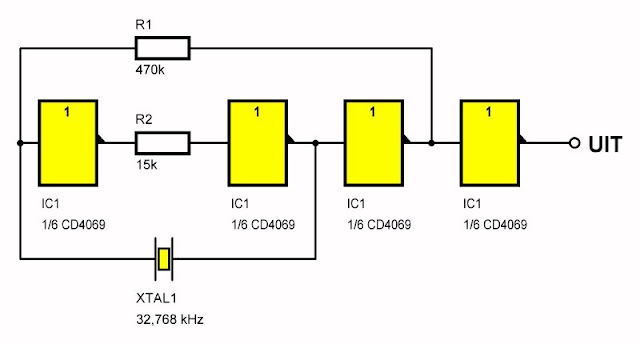 |
| Oscillator met CD4069 poorten. (© 2024 Jos Verstraten) |
Een 1 Hz oscillator
Tot slot een schema van een schakeling waar dit artikel in feite over gaat: een stabiele en nauwkeurige pulsgenerator die om de seconde één puls levert. In de CD4060 zitten 14 van de 15 noodzakelijke frequentiedelers. De laatste deler is een van de twee flip-flop's in een CD4013.
 |
| Oscillator die een één seconde puls levert. (© 2024 Jos Verstraten) |
Koop uw oscilloscoop bij Amazon




