Theorie-11: schakelingen met weerstanden

(gepubliceerd op 21-11-2017)

Weerstanden kunt u in serie en parallel schakelen. Daarnaast besteden wij aandacht aan de theorieën van Kirchhoff, Wheatstone, Thévenin en Norton.

De wet van Ohm

Herhaling van oude kennis
De in het artikel 'Stroom, weerstand en vermogen' besproken wet van Ohm is de basis waarmee u alle mogelijke kringen, die alleen uit spanningsbronnen en weerstanden bestaan, te lijf moet gaan. Vandaar nog even in het kort de betekenis van deze wet. De wet van Ohm stelt dat er een bepaalde evenredigheid bestaat tussen de spanning over een weerstand en de stroom die er doorheen vloeit. Die evenredigheid noemt men de waarde van de weerstand R en wordt uitgedrukt in Ω. In formulevorm kan de wet van Ohm uitgedrukt worden als:
R = U / I

FORMULES IN DIT ARTIKEL
VERMENIGVULDIGEN: Het vermenigvuldigingsteken wordt voorgesteld door een bullet tussen de factoren: a • b = c DELEN: Het gedeeld door teken wordt voorgesteld door een schuine streep: a / b = c

Een bewijs van de wet van Ohm
Deze wet werd door Ohm experimenteel vastgesteld, maar kan ook door zuiver redeneren achterhaald worden. Daarvoor wordt gebruik gemaakt van het schemaatje dat in onderstaande figuur is getekend. Als u een weerstand R aansluit op een spanningsbron met een elektromotorische kracht E, dan ontstaat er over de weerstand een spanningsval die gelijk is aan U. Als gevolg hiervan gaat er door de weerstand een stroom I vloeien. Als de elektromotorische kracht van de spanningsbron groter wordt, dan neemt de kracht op de vrije elektronen toe. Uit de algemene wetten van de mechanica volgt dan dat de snelheid van de elektronen groter wordt. Er vloeien dus per seconde meer elektronen door de kring, hetgeen betekent dat de stroom stijgt.

• Besluit 1: De stroom door de kring is dus evenredig met het spanningsverschil in de keten.

Neemt echter de weerstand toe, dan worden de elektronen geremd. Hun snelheid neemt af en de stroom zal dalen.

• Besluit 2: De stroom door de kring is dus omgekeerd evenredig met de weerstand. 

Beide conclusies kunt u wiskundig uitdrukken door de formule:
I = U / R
of, door I en R van plaats te verwisselen:
R = U / I

Aan de hand van dit schemaatje kunt u de experimentele
wet van Ohm ook beredeneren. (© 2017 Jos Verstraten)

Weerstanden in serieschakeling

Twee weerstanden in serie
Bij de serieschakeling van twee weerstanden, zoals getekend in onderstaande figuur, is één ding onmiddellijk duidelijk. Er vloeit maar één stroom I door de keten, zodat beide weerstanden door dezelfde stroom worden doorlopen.

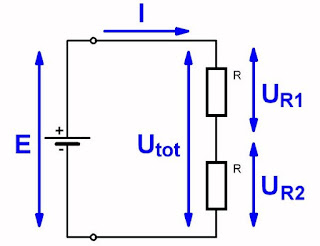De serieschakeling van twee weerstanden. (© 2017 Jos Verstraten)

Op iedere weerstand kunt u de wet van Ohm toepassen:
UR = I • R
De totale spanning over de serieschakeling is gelijk aan de som van de potentiaalverschillen over iedere afzonderlijke weerstand:
Utot = UR1 + UR2
Of:
Utot = [I • R1] + [I • R2]
Hierin kunt u de factor I uit de haakjes bevrijden:
Utot = I • [R1 + R2]
Maar anderzijds is:
Utot = I • Rtot
Uit beide laatste formules kunt u gemakkelijk afleiden:
I • Rtot = I • [R1 + R2]
De stroom I kunt u links en rechts uit de vergelijking schrappen:
Rtot = R1 + R2

Bij de serieschakeling van weerstanden is de totale weerstand gelijk aan de som van de in serie geschakelde weerstanden.

Spanningsdeling
Een serieschakeling van weerstanden wordt in de elektronica vaak toegepast om spanningsdelers te maken. Stel dat u een voedingsspanning van 10 V ter beschikking hebt, maar op een bepaald punt behoefte hebt aan een spanning van 4 V. Uit de 10 V kunt u gemakkelijk een spanning van 4 V afleiden door twee weerstanden in serie te schakelen. Door een bepaalde weerstandsverhouding te kiezen zal op het knooppunt tussen beide weerstanden de gewenste spanning van 4 V ontstaan. Hoe u een dergelijke spanningsdeler moet berekenen volgt weer uit de bovenstaande figuur en de wet van Ohm.
De spanning over de weerstand R2 is gelijk aan:
UR2 = I • R2
De stroom door de kring wordt bepaald door:
I = U / Rtot
Als u deze waarde in de vorige formule invult, ontstaat:
UR2 = U • [R2 / Rtot]
Hieruit volgt weer:
UR2 • Rtot = U • R2
Of:
R2 = [UR2 • Rtot] / U
De waarden van U en UR2 zijn bekend, namelijk 10 V en 4 V. Het volstaat nu een waarde voor de totale weerstand Rtot te kiezen, bijvoorbeeld 10 kΩ om onmiddellijk de waarde van R2 te kunnen berekenen. In dit geval is deze weerstand gelijk aan 4 kΩ, zodat de waarde van R1 gelijk moet zijn aan 6 kΩ.

Een voorbeeld van een spanningsdeler
Dergelijke resistieve spanningsdelers worden vaak toegepast in de elektronica. Als u bijvoorbeeld een digitale voltmeter met een eigen bereik van 1 V volle schaal geschikt wilt maken voor het meten van hogere spanningen, moet u er een serieschakeling van weerstanden voorschakelen. In onderstaande figuur is een dergelijke spanningsdeler getekend. Door de selectie van de weerstandswaarden op 100 kΩ, 900 kΩ en 9 MΩ ontstaan op de twee knooppunten spanningen die gelijk zijn aan een tiende en een honderdste van de ingangsspanning.
Als u dus een spanning van 95 V over de serieschakeling aanlegt, zullen op de twee knooppunten spanningen van 9,5 V en 0,95 V ontstaan. Door de ingang van de digitale meter te verbinden met het knooppunt tussen R2 en R3 zal de ingangsspanning van 95 V gemeten worden als 0,95 V. Het volstaat nu met een tweede schakelaarsectie de decimale punt van de uitlezing om te schakelen naar de juiste positie tussen de drie display's.

Een resistieve spanningsdeler wordt bijvoorbeeld gebruikt om het meetbereik van een
digitale voltmeter uit te breiden. (© 2017 Jos Verstraten)

Opmerking
Bij dit en volgend voorbeeld wordt uitgegaan van een voltmeter met een zeer hoge ingangsweerstand, die de spanningsdeler niet beïnvloedt.

Praktische schakeling van een ingangsdeler
In onderstaande figuur is een praktische schakeling getekend die u bij alle digitale universeelmeters kunt aantreffen. Het enige verschil met het schema van de vorige figuur is dat een deel van de serieschakeling wordt gebruikt voor het meten van stromen.
Ook hier is het de wet van Ohm die de werking van de stroommeter bepaalt. Als u de stroombereik-omschakelaar in de stand 2 mA zet, zal de stroom die aan de mA-ingang (onder) wordt aangeboden door de serieschakeling van de weerstanden van 90 Ω, 9 Ω, 0,9 Ω en 0,1 Ω vloeien. De vervangingswaarde van deze serieschakeling is 100 Ω. Een stroom van 1,25 mA wekt over deze weerstand een spanningsval van 125 mV op. Deze spanning gaat via een van de standen van de spanningsbereik-omschakelaar naar de ingang van het voltmeter-module. De te meten stroom is dus omgezet in een spanning, die numeriek gelijk is aan de waarde van de stroom.

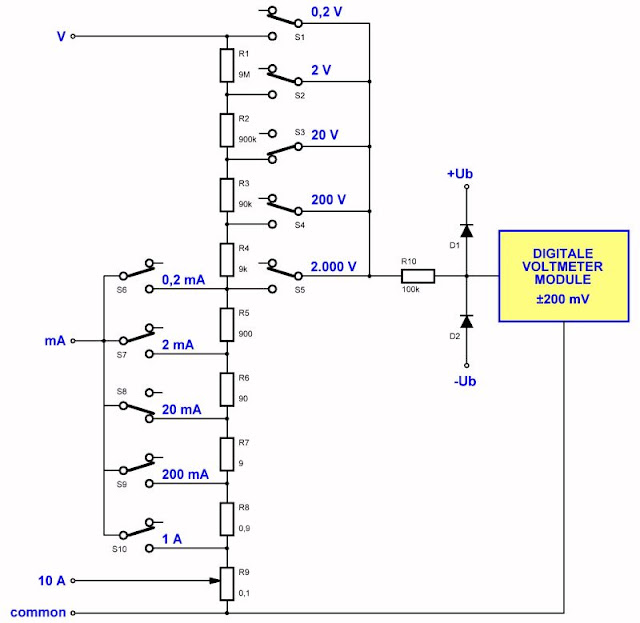Een praktische toepassing van de serieschakeling van weerstanden. (© 2017 Jos Verstraten)

De potentiometer
De potentiometer is de ultieme vorm van een spanningsdeler. Zoals uit onderstaande figuur blijkt, is een potentiometer niets anders dan een serieschakeling van twee weerstanden, waarbij de loper is verbonden met het knooppunt van beide weerstanden. Door het verdraaien van de loper wordt de verhouding tussen beide deelweerstanden continu veranderd. Een potentiometer is dus een spanningsdeler, waarbij u de deelverhouding continu kunt instellen tussen 1 en 0.

Een potentiometer is een serieschakeling van twee weerstanden, waarvan de verhouding continu ingesteld kan worden.
(© 2017 Jos Verstraten)

Weerstanden in parallelschakeling

Twee weerstanden parallel geschakeld
Weerstanden staan parallel, als zij op dezelfde spanningsbron zijn aangesloten. In onderstaande figuur is de parallelschakeling van twee weerstanden R1 en R2 getekend. Ook nu moet de vraag beantwoord worden hoe groot de totale vervangingsweerstand Rtot is.

De parallelschakeling van twee weerstanden. (© 2017 Jos Verstraten)

Het zal duidelijk zijn dat de totale stroom Itot gelijk is aan de som van de stromen die door de twee weerstanden vloeien:
Itot = I1 + I2
U kunt de stromen uitdrukken door de wet van Ohm toe te passen:
U / Rtot = [U / R1] + [U / R2]
Als u linker en rechter uitdrukking deelt door U ontstaat:
1 / Rtot = [1 / R1] + [1 / R2]
Dit is de algemene uitdrukking waaraan de parallelschakeling van weerstanden voldoet. Als u n weerstanden parallel schakelt is de totale vervangingsweerstand gelijk aan:
1 / Rtot = [1 / R1] + [1 / R2] + ..... + [1 / Rn]
In het geval van twee parallel geschakelde weerstanden kunt u deze formule echter iets handiger schrijven. Als u zich uit uw schooltijd herinnert hoe u twee breuken met ongelijke noemer kunt optellen, weet u dat:
Rtot = [R1 • R2] / [R1 + R2]

De vervangingsweerstand van twee parallel geschakelde weerstanden is gelijk aan hun product gedeeld door hun som.

Stroomdeling
Het bespreken van de serieschakeling van weerstanden leidde tot het begrip spanningsdeling. Op dezelfde manier leidt de parallelschakeling tot het begrip stroomdeling. Zoals reeds geschreven deelt de totale stroom Itot zich bij een parallelschakeling in twee deelstromen I1 en I2. Het is, alweer met de wet van Ohm, mogelijk om aan te tonen dat de stromen zich omgekeerd verhouden als de weerstanden. Dus:
I1 / I2 = R2 / R1
Door de grootste weerstand vloeit de kleinste stroom, door de kleinste weerstand de grootste. Als R1 drie keer groter is dan R2, dan zal I1 drie keer kleiner zijn dan I2. Door alweer de wet van Ohm toe te passen en enige berekeningetjes te maken kunt u aantonen dat:
I1 = Itot • [R2 / (R1 + R2)]
en:
I2 = Itot • [R1 / (R1 + R2)]



Praktijkvoorbeeld van stroomdeling: shunt-weerstand berekenen
Deze formules komen in de praktijk van pas om bijvoorbeeld het volgende probleem op te lossen. Stel dat u een gestabiliseerde 12 V voeding bouwt die een uitgangsstroom van 1 A kan leveren. Nu wilt u deze stroom meten. U kunt dan natuurlijk een draaispoelmetertje kopen met een bereik van 1 A. Maar toevallig hebt u in de rommelkist nog een oud metertje liggen met een bereik van 1 mA. Dank zij de formules van de stroomdeling kunt u deze meter toch gebruiken om de gewenste stroom van 1 A te meten. Aan de hand van het schema van onderstaande figuur wordt een en ander duidelijk.

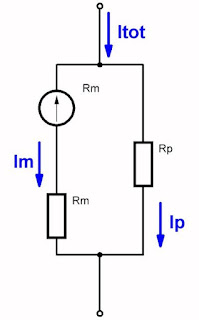Een praktisch voorbeeld van de formules van de stroomdeling.
(© 2017 Jos Verstraten)

De meter heeft uiteraard een bepaalde inwendige weerstand, voorgesteld door Rm. Als het goed is, staat de waarde van deze weerstand op de achterzijde van de draaispoelmeter. De totale stroom Itot van 1 A zal zich splitsen in twee deelstromen. De stroom Im door de meter moet 1 mA groot zijn, zodat de stroom door de parallelweerstand Rp gelijk moet zijn aan 999 mA. U kent nu drie grootheden uit de uitdrukking:
Im / Ip = Rp / Rm
zodat u zonder enige moeite de enige ontbrekende grootheid Rp kan berekenen:
Rp = [Im • Rm] / Ip
Een dergelijke weerstand, die parallel over een draaispoelmeter wordt geschakeld om het stroombereik te vergroten noemt men een 'shunt-weerstand'.

De wetten van Kirchhoff

Kirchhoff ontdekte twee netwerk wetten
De Duitse natuurkundige Robert Gustav Kirchhoff paste in de jaren 1845 en 1846 de wet van Ohm toe op ingewikkelde netwerken van spanningsbronnen en weerstanden. Hij ontdekte twee wetmatigheden die als volgt kunnen worden samengevat.

De eerste wet van Kirchhoff
In ieder knooppunt van een netwerk is de hoeveelheid elektriciteit die in één seconde naar dit punt toevloeit exact gelijk aan de hoeveelheid elektriciteit die in dezelfde tijd van dat punt wegstroomt.
Hoeveelheid elektriciteit per seconde kunt u zonder problemen vertalen naar grootte van stromen. De eerste wet van Kirchhoff stelt dus dat in ieder punt de som van de naar dat punt toevloeiende stromen gelijk is aan de som van de stromen die van dat punt wegvloeien. Vertaald naar het voorbeeld van onderstaande figuur betekent dit:
I1 = I2 + I3 + I4 + I5

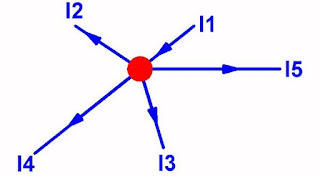De eerste wet van Kirchhoff in de praktijk. (© 2017 Jos Verstraten)

De tweede wet van Kirchhoff
In een gesloten lus van een netwerk is de algebraïsche som van alle aanwezige emk's en spanningsvallen gelijk aan nul. Dat 'algebraïsch' wil zeggen dat u aan de emk's en spanningsvallen een plus- of minteken moet toekennen. Als u de lus bijvoorbeeld doorloopt in uurwijzerzin moet u een emk of spanningsval positief rekenen als u eerst de negatieve en nadien de positieve pool tegenkomt.
Andersom, als u eerst de positieve pool en nadien de negatieve pool ontmoet, moet u de emk of spanningsval negatief rekenen. In het in onderstaande figuur getekende voorbeeld betekent dit dus:
E3 - E5 - E2 = 0
In dit voorbeeld zijn voor de eenvoud alleen drie spanningsbronnen met hun emk's opgenomen. Maar als er in de gesloten lus ook weerstanden aanwezig zijn, dan moet u de spanningsvallen daarover ook in de optelling opnemen.

De tweede wet van Kirchhoff in de praktijk. (© 2017 Jos Verstraten)

Een rekenvoorbeeld van de wetten van Kirchhoff
De twee wetten van Kirchhoff geven u een handige methode om stromen en spanningen in ingewikkelde netwerken te berekenen. Als voorbeeld wordt het netwerkje van onderstaande figuur behandeld. De vraag is hoe groot de stromen zijn die door de drie weerstanden vloeien.
In het netwerkje kunt u drie gesloten lussen herkennen, namelijk 1, 2 en 3. Verder kunt u een knooppunt A onderscheiden, waar drie stromen samen komen. Aan die drie stromen kunt u willekeurige richtingen toekennen, bijvoorbeeld I1 naar punt A toe en I2 en I3 van het punt af. Als uit de berekening een
negatieve waarde van een stroom volgt, weet u dat de werkelijke richting omgekeerd is aan de gekozen.
In punt A kunt u de eerste wet toepassen, zodat:
I1 = I2 + I3 (1)
Als u de tweede wet toepast op de gesloten lus 1 ontstaat:
10 - [5 • I1] - [2 • I2] = 0 (2)
Dezelfde wet toegepast op de buitenste lus 2 geeft:
10 - [5 • I1] + 6 - [3 • I3] = 0 (3)
Er ontstaat een stelsel van drie vergelijkingen met drie onbekenden. Met wat eenvoudige wiskunde kunt u dit stelsel oplossen. Het volstaat in de tweede vergelijking I2 uit te drukken als functie van I1 en in de derde vergelijking I3 uit te drukken in functie van I1. Nadien kunt u deze waarden van I2 en I3 weer invullen in de eerste vergelijking, zodat deze nog maar één onbekende I1 bevat. Hieruit volgt dat I1 = 2 A.
Door nu de berekende waarde van I1 in te vullen in de tweede en derde vergelijking kunt u de waarden van I2 en I3 berekenen, met respectievelijk 0 A en 2 A als resultaat. Ter bevestiging kunt u de eerste wet van Kirchhoff in punt A nog even controleren:
2 A = 0 A + 2 A

Met de wetten van Kirchhoff kunt u alle stromen in dit netwerkje berekenen.
(© 2017 Jos Verstraten)

Rekenregels
De toepasbare rekenregeltjes voor het oplossen van dergelijke vergelijkingen op een rijtje gezet:

• Als u een term van links naar rechts gooit of andersom, verandert het teken. Dus A + B = C + D kan ook geschreven worden als A + B - C = D.
• Aan een vergelijking verandert niets als u links en rechts met hetzelfde getal vermenigvuldigt of door hetzelfde getal deelt. Dus de vergelijking A = 5 • B is hetzelfde als 5 • A = 25 • B.
• In een breuk kunt u teller en noemer met hetzelfde getal vermenigvuldigen. De breuk A / [2 • B] is dus gelijk aan de breuk [2 • A] / [4 • B].

Besluit
De twee wetten van Kirchhoff hebben een groot praktisch nut. Aan de hand van deze wetten kunt u ingewikkelde verzwakkernetwerken, zoals T- of Pi-netwerken, vrij eenvoudig berekenen. In onderstaande figuur is als voorbeeld een verzwakker getekend, die samengesteld is uit vijf Pi-netwerken. De bedoeling is dat ieder netwerk het ingangssignaal met een bepaalde dB-factor verzwakt.

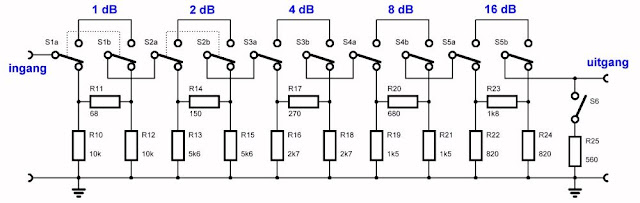Dergelijke verzwakker netwerken kunt u volledig berekenen als u de wetten van Kirchhoff onder de knie hebt.
(© 2017 Jos Verstraten)

De wet van Wheatstone

De bekendste brug
Wheatstone wordt algemeen erkend als de uitvinder van de brugschakeling, hoewel zuiver historisch bekeken deze eer eerder toekomt aan Samuel Christie. Hoe dan ook, de schakeling die in onderstaande figuur is getekend staat algemeen bekend als 'brug van Wheatstone'. Deze brug bestaat uit vier weerstanden, die een gecombineerde serie/parallel-kring vormen die is aangesloten op een spanningsbron Uin. De wet van Wheatstone zegt nu dat de spanning tussen de knooppunten C en D gelijk is aan nul, als er aan de volgende gelijkheid wordt voldaan:
R1 / R2 = R3 / R4
Men zegt dan dat de brug in evenwicht is.

De brug van Wheatstone. (© 2017 Jos Verstraten)

Nauwkeurig weerstanden meten
Deze schakeling wordt vaak toegepast in de elektronica. Een van de voor de hand liggende toepassingen is het meten van weerstanden. Als u de onbekende weerstand Rx in een van de vier takken van de brug opneemt en de verhouding van de weerstanden R2 en R3 in de andere tak regelbaar maakt, zie onderstaande figuur, dan kunt u de waarde van de onbekende weerstand heel nauwkeurig bepalen. Het volstaat een zeer gevoelige stroommeter tussen de diagonaal A/C van de brug op te nemen en de geijkte verhouding tussen R2 en R3 zo te regelen tot er geen stroom door de meter vloeit. De brug is dan in evenwicht. Uit de bekende waarden van de vaste weerstand R4 en de instelbare weerstanden R2 en R3 kunt u met de wet van Wheatstone onmiddellijk de waarde van de onbekende weerstand Rx berekenen.

Een praktische toepassing van de wet van Wheatstone: het nauwkeurig meten
van een onbekende weerstand Rx. (© 2017 Jos Verstraten)

Het begrip inwendige weerstand

Emk en klemspanning
Een spanningsbron wordt niet alleen gekenmerkt door zijn emk, maar ook door zijn inwendige weerstand Rinw. Het gevolg hiervan is dat u niet zonder meer kunt stellen dat de bron een spanning levert die gelijk is aan zijn emk. U moet twee spanningsdefinities invoeren, namelijk een in een toestand waarin de bron niet wordt belast en een in een toestand waarin de bron wél wordt belast. Het verschil valt te verklaren uit het schema van onderstaande figuur. De spanningsbron wordt voorgesteld door de serieschakeling van een ideale bron E en de inwendige weerstand Rinw. Als de bron niet belast is zal er geen stroom doorheen vloeien, met als gevolg dat er geen spanning over de inwendige weerstand valt. De uitgangsspanning Uk van de bron is dan gelijk aan E, de emk van de bron. Als u de bron echter belast door een weerstand Rlast, dan ontstaat er een serieschakeling van Rinw en Rlast. Het gevolg is dat er een stroom doorheen gaat vloeien die over de inwendige weerstand een bepaalde spanning opwekt. De uitgangsspanning Uk is dan niet meer gelijk aan de waarde van E, maar zal lager zijn.
De waarde van Uk wordt de 'klemspanning' van de bron genoemd omdat dit de spanning is die u in de praktijk tussen de klemmen van de bron meet. De klemspanning is gelijk aan:
Uk = E - [I • Rinw]

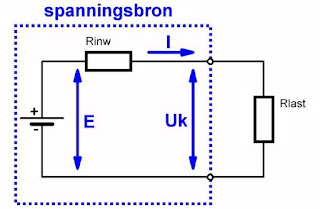Het begrip inwendige weerstand van een spanningsbron grafisch toegelicht.
(© 2017 Jos Verstraten)

Aanpassing
Een belangrijk gevolg van de aanwezigheid van de inwendige weerstand is dat het vermogen dat u uit een spanningsbron kunt halen afhankelijk is van de verhouding tussen de inwendige weerstand en de belastingsweerstand. Dat is een belangrijk gegeven, omdat het in de praktijk er vaak op aan komt zoveel mogelijk vermogen uit een bron te halen. Denk bijvoorbeeld aan een audio eindversterker. Zo'n schakeling kunt u opvatten als een wisselspanningsbron die vermogen aan de belasting, de luidspreker, levert. Uiteraard heeft deze eindversterker een bepaalde inwendige weerstand. Het komt er nu op aan de weerstand van de luidspreker zo te kiezen dat de versterker zoveel mogelijk vermogen aan de luidspreker kan leveren.
Men noemt dit 'het aanpassen van de belasting aan de bron'.
U kunt gemakkelijk inzien dat er twee waarden van de belasting zijn, waarbij de bron géén vermogen levert. Zoals u weet wordt het elektrisch vermogen dat in een weerstand wordt gedissipeerd gegeven door de formule:
P = I² • R
Vervangt u de weerstand door de verhouding tussen spanning en stroom, dan ontstaat:
P = I² • [U / I]
Of:
P = I • U
Als de belastingsweerstand nul is, is de spanning over die weerstand ook nul met als logisch gevolg dat het vermogen nul is. Als de belastingsweerstand oneindig hoog is vloeit er geen stroom doorheen, alweer met als gevolg dat het vermogen nul is. Tussen die twee nulwaarden zal het van bron naar belasting overgedragen vermogen een verloop hebben als geschetst in de onderstaande figuur. Hieruit blijkt dat het maximale vermogen van bron naar belasting wordt overgedragen als de belastingsweerstand precies gelijk is aan de inwendige weerstand. Wiskundig uitgedrukt:
Rlast / Rint = 1
Een zeer belangrijke wet! Dank zij deze wet kunt u schakelingen die vermogen moeten leveren optimaliseren.

Het verband tussen waarde van de belastingsweerstand en de grootte van het tussen
bron en belasting overgedragen vermogen. (© 2017 Jos Verstraten)

Meten van de inwendige weerstand
Natuurlijk komt het er op aan de inwendige weerstand van een spanningsbron te kennen. Die kunt u eenvoudig meten aan de hand van het schema van de vorige figuur. Eerst meet u de klemspanning zonder belastingsweerstand. Nadien sluit u een bekende weerstand aan over de bron en meet weer de uitgangsspanning. Die zal lager zijn, dat is een zaak die duidelijk is. U kent nu de klemspanning en de waarde van de belastingsweerstand, dus u kunt de stroom berekenen met de wet van Ohm. Uit het verschil tussen beide metingen weet u ook de spanningsval over de inwendige weerstand Rint. U weet de stroom, uit de kennis van spanningsval en stroom kunt u de waarde van Rint berekenen.
Een voorbeeldje.
Stel dat de onbelaste spanning gelijk is aan 10 V. Als u de bron belast met een weerstand van 1 kΩ zakt de klemspanning tot 9 V. Op dat moment vloeit er een stroom van 9 V gedeeld door 1 kΩ is gelijk aan 9 mA door de kring. Deze stroom wekt over de inwendige weerstand een spanning op van 10 V minus 9 V is gelijk aan 1 V. De inwendige weerstand is dus 1 V gedeeld door 9 mA is gelijk aan 111,11 Ω.

Het theorema van Thévenin

Opstellen van equivalente schakelingen
Het theorema van Thévenin geeft een handige methode om netwerken, die bestaan uit spanningsbronnen en weerstanden, te vereenvoudigen. Thévenin stelde dat iedere gesloten lus in een netwerk vervangen kan worden door de serieschakeling van een zuivere emk-spanningsbron en een serieweerstand. Die eenvoudige schakeling zal zich dan, naar de buitenwereld toe, net zo gedragen als de oorspronkelijke gesloten lus. In de elektronica spreekt men van 'het opstellen van een equivalente schakeling', een belangrijke methode om ingewikkelde schakelingen te vereenvoudigen tot zij zeer inzichtelijk zijn geworden.


Een eenvoudige voorbeeld
In onderstaande figuur wordt dit theorema op een eenvoudig voorbeeldje toegepast. In deze figuur is uiterst links een gesloten lus getekend, die deel uitmaakt van een ingewikkeld netwerk. Die gesloten lus is via de punten A en B met de rest van dat netwerk verbonden. Uiterst rechts is getekend hoe Thévenin deze gesloten lus vereenvoudigt tot één emk-bron en één serieweerstand. Het omzetten gaat in twee fasen, waarbij u de wetten van Kirchhoff moet toepassen.

Een eenvoudig voorbeeld waarmee het theorema van Thévenin wordt toegelicht. (© 2017 Jos Verstraten)

Fase 1
Bereken de spanning die tussen de punten A en B aanwezig is, zonder dat de lus door iets anders belast wordt. In het eenvoudige voorbeeld blijkt onmiddellijk dat de spanning tussen de punten A en B gelijk is aan 4,5 V.

Fase 2
Vervang alle spanningsbronnen in de gesloten lus door een kortsluiting en bereken dan de weerstand die tussen de punten A en B gemeten kan worden. In dit simpele voorbeeld is het overduidelijk dat die weerstand gelijk is aan 50 Ω, want als u de bron kortsluit staan de twee weerstanden van 100 Ω parallel geschakeld. De gesloten lus kan nu vervangen worden door een equivalent schema, bestaande uit de berekende spanningsbron in serie met de berekende weerstand.

Het theorema van Norton

Nu geen spanningsbron, maar een stroombron
Ook het theorema van Norton is een methode om ingewikkelde gesloten lussen te vervangen door eenvoudigere equivalente schakelingen. Nu bestaat de equivalente schakeling echter uit de parallelschakeling van een stroombron en een weerstand. In onderstaande figuur wordt als voorbeeld dezelfde gesloten lus als die van het vorige voorbeeld omgezet in een Norton-schakeling. Ook nu gaat het omzetten in twee fasen.

Het omzetten van een gesloten lus in een Norton-equivalent. (© 2017 Jos Verstraten)

Fase 1
Sluit de klemmen A en B van de gesloten lus kort en bereken de stroom die in deze kortsluiting zal lopen. Dit is voorgesteld in het middelste schema van de figuur. In het voorbeeld zal de stroom gelijk zijn aan 9 V gedeeld door 100 Ω, dus 90 mA. Deze stroom wordt Io genoemd.

Fase 2
Bereken nu weer de totale weerstand van de gesloten lus, door alle spanningsbronnen kort te sluiten en middels de wetten van Kirchhoff de vervangingsweerstand tussen de punten A en B te berekenen. Deze weerstand wordt Ri genoemd. In het voorbeeld is deze weerstand gelijk aan 50 Ω. Het Norton-equivalent van de gesloten lus bestaat dus uit de parallelschakeling van een stroombron die 90 mA levert en een weerstand van 50 Ω.

Thévenin en Norton in de praktijk

Voer voor theoretici?
Beide theorema's lijken op het eerste zicht voer voor theoretici. Dat is echter absoluut niet het geval. Met Thévenin en Norton kunt u bijvoorbeeld een transistortrap voorstellen door een vierpool, waar de vier parameters van de halfgeleider h11, h12, h21 en h22 in verwerkt zijn. Uit deze figuur blijkt duidelijk dat de ingangskring (basis) kan gereduceerd worden tot een Thévenin-equivalent, bestaande uit een weerstand en een spanningsbron. De uitgangskring (collector) kan voorgesteld worden door een Norton-equivalent, opgebouwd uit een stroombron en een weerstand. Dank zijn deze vereenvoudigingen tot equivalenten is het mogelijk de eigenschappen van de trap, zoals versterkingsfactor, ingangs- en uitgangsimpedantie, gemakkelijk te berekenen.

Praktische toepassing van de theorema's van Thévenin en Norton: het voorstellen van een transistortrap door een vierpool.
(© 2017 Jos Verstraten)

Besluit

Als u ooit de behoefte voelt om wiskundig te gaan stoeien met netwerken, kunt u niet om de Heren Kirchhoff, Wheatstone, Thévenin en Norton heen!



(Banggood sponsor advertentie)
375 elco's, 15 x 25 waarden