Know-how: glasvezel kabels

(gepubliceerd op 09-08-2023)

Een groot deel van Nederland is al 'verglaasd' en men is druk bezig ook de buitengebieden aan de glasvezel kabel te hangen. Maar hoe werkt dit medium, wat zijn de eigenschappen en welke soorten bestaan er?

Een historische inleiding

Zonder laser geen glasvezel communicatie
De moderne glasvezel communicatie zou niet denkbaar zijn zonder de uitvinding van de laser in 1960. Deze 'Light Amplification bij Stimulated Emission of Radiation' is een revolutionaire lichtbron, met zeer speciale eigenschappen. Een laser zendt een zeer dunne lichtstraal uit met een zo goed als monochromatische samenstelling. Dat wil zeggen dat de elektromagnetische straling waaruit het licht bestaat bijna zuiver sinusvormig verloopt op één welbepaalde frequentie. Die frequentie is zeer hoog, gemiddeld ligt deze rond 3 x 10¹⁴ Hz, oftewel 300 THz. Als een dergelijke hoge frequentie wordt gemoduleerd kan een immense hoeveelheid gegevens worden verzonden. Hoe hoger immers de frequentie van een draaggolf, hoe meer laagfrequentere gegevens er in verwerkt kunnen worden.
Een tweede gunstige ontwikkeling was dat fotogevoelige detectoren ter beschikking stonden die de gemoduleerde laserbundel weer in een elektrisch signaal konden omzetten.

De eerste experimenten
De eerste experimenten met het verzenden van gegevens via een lichtbundel werden uitgevoerd in de open lucht. Helaas bleek dat de aardse atmosfeer een te onbetrouwbaar medium is voor het langs optische weg verzenden van gegevens. Spelbrekers waren uiteraard regen en mist. Vervolgens werden experimenten uitgevoerd met holle, gespiegelde buizen als transportmedium. Dit kon wel, maar dan moesten om de zoveel honderd meter lenzen in de buizen worden aangebracht om het laserlicht weer te bundelen. Ook dit was geen praktisch bruikbare oplossing.

Professor van Heel van de Technische Universiteit Delft
De communicatie via glasvezel kwam onder de aandacht van de technici naar aanleiding van een artikel van de Nederlandse professor Bram van Heel van de Technische Universiteit van Delft. Hij staat bekend als de 'vader van de technische optica in Nederland' en was mede-oprichter van 'Optische Industrie De Oude Delft' en 'Nonius'. Bram van Heel beschreef in 1953 op zuiver theoretische basis een systeem voor optische communicatie, waarbij laserlicht werd voortgeplant via een dunne glazen kern, omgeven door een mantel. Experimenten die werden uitgevoerd slaagden niet. De technologie kon geen dunne glasvezels maken die voldeden aan de extreme optische eisen die voor glasvezel communicatie nodig waren. De laserstraal werd te zeer verzwakt in de glaskern, waardoor geen praktisch bruikbare afstanden konden worden overbrugd. 

Professor van Heel, Technische Universiteit Delft.
(© Wikimedia Commons)

In 1966 kwam een belangrijke doorbraak
Twee onderzoekers, Kuen Kao en Hockman, publiceerden een artikel waarin een verklaring werd gegeven voor de grote verzwakking van het laserlicht in de glaskernen. Het waren voornamelijk kleine waterverontreinigingen in het glas die de oorzaak waren van de grote verzwakking. Op zuiver theoretische gronden toonden zij aan dat het met optisch zeer zuiver glas, getrokken tot μm dunne vezels, mogelijk moest zijn afstanden tot 2 km te overbruggen met verliezen van slechts enige tientallen dB.
Aan de hand van dit theoretisch artikel werden de experimenten weer opgepakt. Veel energie en onderzoek werd besteed aan het verbeteren van de eigenschappen van het glas en het minimaliseren van de diameter van de vezels. In 1970 kwam een Amerikaans bedrijf op de markt met een glasvezel kabel die slechts 15 dB/km verzwakte. In datzelfde jaar ontwikkelde Bell de eerste stabiele en goed bruikbare halfgeleidende laser die gemakkelijk moduleerbaar was. In 1977 werd de eerste praktische glasvezelverbinding met een lengte van 10 km aangelegd tussen de Engelse steden Stevenhage en Hitchin. De gebruikte kabel had een verlies van 5 dB/km, hetgeen toch nog het inzetten van versterkers noodzakelijk maakte.

De situatie nu
Sindsdien zijn de ontwikkelingen in snel tempo gegaan! Op dit moment bestaan er glasvezel kabels waarvan de actieve kern een diameter van slechts 3 μm (drie duizendsten van een millimeter!) heeft en die een verzwakking van slechts 0,15 dB/km veroorzaken. Met dergelijke kabels zijn, zonder versterking, afstanden tot 200 km te overbruggen.

Het principe van communicatie via de glasvezel kabel

Inleiding
Uiteraard bestaan er nog geen systemen die gegevens, zoals spraak, rechtstreeks omzetten in gemoduleerd licht. De basis van optische communicatie is dus nog steeds de elektronica. Bij de ontvanger doet zich dezelfde situatie voor. Het gemoduleerde licht kan niet rechtstreeks begrepen worden. Ook daar moeten elektronische schakelingen gebruikt worden om het gemoduleerde licht weer in elektronische signalen om te zetten.
Een communicatiesysteem via een glasvezel kabel bestaat, zoals getekend in de onderstaande figuur, uit drie delen. Links is de 'zender' getekend, die het te verzenden digitale elektronische signaal versterkt en de digitale pulsen aanbiedt aan de 'lichtzender'. Tegenwoordig bestaat deze steeds uit een kleine halfgeleidende laser. Voor kleine afstanden kan echter ook gebruik worden gemaakt van een infrarode LED. Het licht dat deze bron uitstraalt wordt via een speciale koppeling in de glasvezel kabel geleid. De optische pulsen zijn op dit moment nog zeer scherp. Maar door de transmissie door de kabel zal er toch een bepaalde pulsvervorming optreden. Aan de ontvanger zijde zijn de optische pulsen niet meer zo scherp, maar enigszins uitgesmeerd in de tijd. De flanksteilheid neemt behoorlijk af. Het zal duidelijk zijn dat dit verschijnsel het aantal pulsen dat per seconde kan worden verzonden beperkt. Via een identieke koppeling wordt het einde van de glasvezel gekoppeld met een fotogevoelige detector, in de meeste gevallen een fotodiode. Deze diode zet de lichtpulsen weer om in elektronische pulsen, die via geëigende schakelingen naar mooie digitale signalen worden getransformeerd.
Het unieke van glasvezel communicatie is dus dat er slechts één ader voor nodig is! Dit in tegenstelling tot elektronische communicatie, waar uiteraard steeds twee aders nodig zijn voor het overbrengen van signalen: een 'hete' ader en een 'koude' ader, ook wel eens de massa genoemd, of twee 'symmetrische' aders.

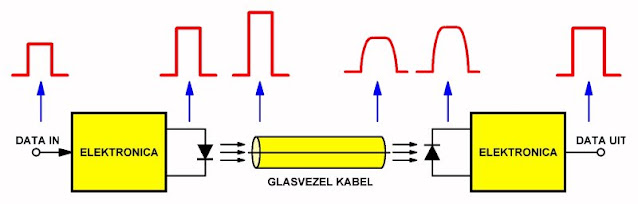Het principe van optische communicatie via een glasvezel kabel. (© 2023 Jos Verstraten)

De voordelen van communicatie via een glasvezel kabel
       - Heeft zeer grote bandbreedtes.
       - Maakt zeer hoge snelheden mogelijk.
       - Kan grote afstanden overbruggen.
       - Is volledig ongevoelig voor elektrische en magnetische stoorvelden.
       - Geeft een absolute elektrische isolatie tussen de apparaten.
       - Is lichtgewicht (30 meter slechts 2 kg, koper 20 kg).
       - Is heel dun, handig in krappe datacenters.
       - Is toekomstbestendig.
       - Heeft geringe kans op diefstal door goedkope grondstof glas.
       - Er is ruime grondstofvoorraad, kabel bestaat voor ongeveer 80 % uit zand.
       - Is veel moeilijker af te tappen dan koper.

De nadelen van communicatie via een glasvezel kabel
       - Er bestaan helaas meer dan veertig soorten connectoren!
       - Het is moeilijker om glasvezel connectoren aan te brengen.

Noodzakelijke optische theorie

Inleiding
Iedere technologie heeft eigen wetmatigheden, gebaseerd op algemene fysische theorieën. Bekende begrippen als impedantie en inwendige weerstand van een kabel zijn absoluut niet van toepassing op glasvezel kabels! Daarvoor in de plaats komen begrippen als modusdispersie, chromatische dispersie, numerieke apertuur en golflengte vensters. Wilt u iets begrijpen van deze specificaties, dan zult u toch op zijn minst een beetje kennis moeten hebben over de fysische optische theorieën die aan deze technologie ten grondslag liggen.

De voortplanting van licht
Licht is een elektromagnetisch verschijnsel dat zich in principe rechtlijnig voortplant door transparante media zoals lucht, glas, etc. In principe, omdat deze wet alleen geldt als het licht zich blijft voortplanten door een en hetzelfde medium. Valt een lichtstraal echter schuin in op het scheidingsvlak van twee transparante stoffen met verschillende optische eigenschappen, dan wordt de lichtstraal gebroken en vervolgt nadien zijn weg weer rechtlijnig door het andere materiaal.
Deze algemene optische wet kunt u controleren door een rechte stok half in stilstaand water te steken. Het lijkt dan net alsof de rechte stok een knik vertoont daar waar hij het water in gaat, zie de onderstaande figuur.
 

Lichtbreking, toegelicht aan de hand van een alledaags voorbeeld.
(© Techna.nl)

De optische dichtheid
Deze lichtbreking wordt veroorzaakt door een bepaalde eigenschap van optisch transparante stoffen, namelijk de 'optische dichtheid'. Deze eigenschap bepaalt de voortplantingssnelheid van het licht door de stof. In het absolute luchtledige bedraagt de voortplantingssnelheid van het licht ongeveer 300.000 km/s. Dit is, voor zover natuurkundigen op dit moment aannemen, de hoogste snelheid die in het heelal is te bereiken. In zuiver water bedraagt de snelheid van een lichtstraal echter slechts 225.000 km/s.
Dit verschil in voortplantingssnelheid, rechtstreeks gevolg van de verschillende optische dichtheden van de stoffen, is verantwoordelijk voor het verschijnsel van lichtbreking.


De brekingsindex η
Iedere optisch transparante stof wordt gekenmerkt door een bepaalde brekingsindex η. Deze factor is gelijk aan de verhouding tussen de voortplantingssnelheid van het licht in het absolute luchtledige en deze in de stof. In formulevorm uitgedrukt:
η = c / v
waarin: 
       - η de brekingsindex is.
       - c de snelheid is van het licht is in het absolute luchtledige. 
       - v de snelheid is van het licht is in de stof.
Uit deze formule kunt u afleiden dat de brekingsindex van zuiver water gelijk is aan:
ηwater = 300.000 / 225.000 = 1,33
De brekingsindex is dus altijd groter dan 1!
De Nederlandse natuurkundige W. Snellius ontdekte reeds in 1621 dat er een eenvoudig wiskundig verband bestaat tussen de brekingsindexen van stoffen en de mate waarin een lichtstraal gebroken wordt, zie ook de onderstaande figuur:
η1 / η2 = (sin β) / (sin α)
of:
η1 ● (sin α) = η2 ● (sin β)
waarin: 
       - η1 de brekingsindex is van de eerste stof. 
       - α de hoek is waarmee de lichtstraal in de eerste stof treedt.
       - η2 de brekingsindex is van de tweede stof. 
       - β de hoek is waarmee de lichtstraal in de tweede stof treedt.

De wet van Snellius. (© 2023 Jos Verstraten)

Breking en reflectie
Op het scheidingsvlak van de twee stoffen zal echter niet alleen breking van de lichtstraal optreden, maar ook een zekere mate van reflectie of terugkaatsing. Een deel van de in de eerste stof invallende lichtstraal wordt onder eenzelfde hoek gereflecteerd in de stof. Deze terugkaatsing wordt de 'fresnelreflectie' genoemd. De verhouding tussen het gereflecteerde deel van het licht en het deel dat gebroken zijn weg vervolgt hangt van een aantal factoren af:
       - In eerste instantie uiteraard van de brekingsindexen van de twee stoffen.
       - In tweede instantie van de grootte van de invalshoek α.
Naarmate de invalshoek α groter wordt zal steeds meer licht worden gereflecteerd en steeds minder licht gebroken zijn weg vervolgen in de tweede stof. Bij een bepaalde waarde van α, de zogenaamde 'kritische invalshoek', zal de volledige lichtstraal op het scheidingsvlak van de twee stoffen worden gereflecteerd.
Dit verschijnsel is het basisprincipe waarmee glasvezel kabels werken!

De eigenschappen van een glasvezel kabel

Inleiding

Een glasvezel kabel heeft geheel andere eigenschappen en specificaties dan een koperen kabel. Ook bekende begrippen, zoals bandbreedte, krijgen bij glasvezel kabels een geheel eigen invulling. In dit hoofdstuk laten wij u kennis maken met de onderstaande eigenschappen van glasvezel kabels:

       - De modi van de voortplanting.

       - De modusdispersie.

       - De dispersievervorming.

       - De chromatische dispersie.

       - De chromatische vervorming.

       - De demping van een glasvezel.

       - De vensters van een glasvezel.

       - De numerieke apertuur.

       - De acceptatie-kegel.

       - De transmissiesnelheid.

       - De bandbreedte.

De samenstelling van een glasvezel kabel
Een glasvezel kabel bestaat steeds uit drie fundamentele delen. Deze zijn getekend in de onderstaande figuur. Allereerst is er de eigenlijke lichtgeleider, dus de glasvezel, ook 'kern' of 'core' genoemd. Deze heeft een diameter tussen 3 μm en 200 μm. De dikte van deze kern, zo zal later blijken, speelt een zeer belangrijke rol en bepaalt in hoge mate de eigenschappen van de glasvezel kabel. De kern is gemaakt van zeer zuiver kwarts.
Rond de kern zit de 'mantel', in de vakliteratuur de 'cladding' genoemd. Ook deze mantel is van kwarts, maar dit kwarts heeft een andere brekingsindex dan de stof waaruit de core is getrokken. De verhouding tussen beide brekingsindexen is zeer kritisch en bepaalt de mate van reflectie van het licht dat door de glasvezel wordt gestuurd.

Rond de cladding zit de bescherming of de 'jacket'. Deze heeft geen principiële functie, maar beschermt de zeer dunne vezel tegen beschadigingen en geeft de vezel de noodzakelijke mechanische stevigheid. Deze jacket is uiteraard niet gemaakt van glas, maar in de meeste gevallen van een of ander kunststof. 

De fundamentele samenstelling van een glasvezel kabel.
(© 2023 Jos Verstraten)

Het basisprincipe van lichtgeleiding in een glasvezel kabel
Aan de hand van de tot nu toe onthulde wetenschap kunt u het basisprincipe van lichtgeleiding door een glasvezel gemakkelijk begrijpen. Dit basisprincipe wordt toegelicht aan de hand van de onderstaande figuur, waarin u een doorsnede door een glasvezel kabel ziet. U moet zich voorstellen dat links een monochromatische lichtbron staat die lichtstralen naar de glasvezel stuurt. Als de lichtbron puntvormig is zullen lichtstralen onder verschillende hoeken in de glasvezel penetreren. 

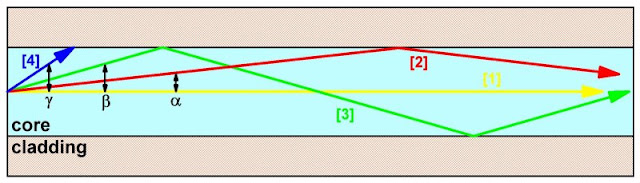Het basisprincipe van lichtgeleiding door een glasvezel kabel. (© 2023 Jos Verstraten)

• Lichtstraal [1] (geel)
  Deze valt in onder een hoek van 0 graden en plant zich dus in de richting van de lengte-as van de vezel voort. In de veronderstelling dat de lichtvezel volledig recht loopt, zal deze straal zich zonder breking of reflectie door de vezel voortplanten. Uiteraard is dit een zuiver theoretisch geval, want geen enkel kabel kan zo recht worden gelegd dat deze situatie zich voordoet. 
• Lichtstraal [2] (rood)
  Deze valt in onder een hoek α. Deze straal zal dus na een bepaalde afstand invallen op het scheidingsvlak tussen de core en de cladding. De invalshoek is echter zo groot dat er volledige fresnelreflectie plaats vindt. Dergelijke stralen zullen zich dus, heen en weer kaatsend door de core, door de glasvezel voortplanten. 
• Lichtstraal [3] (groen)
  Hetzelfde geldt voor lichtstraal [3]. Deze valt de kern binnen onder een hoek β met als gevolg dat de invalshoek tussen core en cladding nog steeds zo groot is dat er nagenoeg volledige reflectie optreedt. 
• Lichtstraal [4] (blauw)
  Deze straal valt echter onder een zo scherpe hoek ɣ in de glasvezel, dat geen reflectie optreedt maar breking. De lichtstraal verdwijnt in de cladding en wordt geabsorbeerd door de jacket. Dergelijke stralen dragen dus niet bij aan het transport van het licht door de kabel. 

De modi van de voortplanting
Uit de bovenstaande figuur volgt dat de lichtstralen [1], [2] en [3] zich weliswaar alle drie door de vezel voortplanten, maar dat de afgelegde weg van deze drie lichtstralen niet gelijk is. Straal [1] plant zich rechtlijnig voort en legt dus de kortste weg af. Straal [2] kaatst heen en weer en legt een iets langere weg af. Straal [3] kaatst vaker heen en weer dan straal [2], met als gevolg dat deze straal de langste weg aflegt.
Nu zijn er natuurlijk tussen een invalshoek van nul graden en een invalshoek van β in principe een oneindig aantal invalshoeken mogelijk. Al deze hoeken leveren lichtstralen op die zich door de vezel voortplanten, maar al deze lichtstralen leggen allemaal een iets andere weg af.
Een lichtstraal kan zich dus via diverse paden door de vezel voortplanten. Deze paden noemt men de 'modi' van de glasvezel. Hoe minder vaak een lichtstraal gereflecteerd wordt in de kabel, hoe lager de modus van deze straal. In het getekende voorbeeld heeft dus lichtstraal [1] de laagste modus en lichtstraal [3] de hoogste modus.

De modusdispersie
Een belangrijk gevolg van de diverse modi is dat lichtstralen, die op hetzelfde tijdstip de lichtvezel binnen dringen, er niet op hetzelfde moment uitkomen. Er ontstaan dus 'looptijdverschillen'. Dat is een logisch gevolg van het feit dat lichtstraal [1] en veel kortere weg aflegt dan lichtstraal [3]. Dit verschijnsel noemt men de 'modusdispersie'.

De dispersievervorming
Een vervelend gevolg van deze modusdispersie is dat een scherpe lichtimpuls, die in de kabel wordt gestuurd, er vervormd zal uitkomen. De mate van vervorming hangt van twee factoren af, namelijk:
       - Het aantal modi dat in de glasvezel kan optreden.
       - De totale looptijdverschillen tussen de modi of de lengte van de kabel.
Hoe dunner de vezel, hoe minder modi er kunnen optreden en hoe kleiner de vervorming zal zijn. Hoe langer de kabel, hoe groter de totale looptijdverschillen tussen de diverse modi zullen zijn en hoe 'uitgesmeerder' een van oorsprong scherpe lichtpuls uit de vezel komt.
Deze dispersievervorming wordt grafisch toegelicht in de onderstaande figuur.

Het verschijnsel dispersievervorming. (© 2023 Jos Verstraten)

De chromatische dispersie
De voortplantingssnelheid van licht door een stof hangt niet alleen af van de reeds genoemde optische dichtheid, maar ook van de golflengte van het licht. U kunt deze eigenschap voorstellen in een grafiek, waarin de looptijd van het licht door het medium, uitgedrukt in μs/km, wordt uitgezet in functie van de golflengte van het licht, uitgedrukt in nm. Voor kwarts is deze grafiek voorgesteld in de onderstaande grafiek.

De looptijd van licht door kwarts. (© 2023 Jos Verstraten)

Dit verschijnsel noemt men de 'chromatische dispersie' van een glasvezel kabel. Nu zou deze eigenschap niet voor problemen hoeven te zorgen als men de beschikking had over een lichtbron die licht van één welbepaalde golflengte, zogenoemd absoluut monochromatisch licht, uitstraalt. Maar een dergelijke lichtbron bestaat niet! Zelfs een laser, waarvan wordt gezegd dat deze monochromatisch is, voldoet niet geheel en al aan deze eigenschap. Het door een laser uitgezonden licht heeft tóch een bepaalde golflengtespectrum, hetgeen betekent dat het uitgezonden licht uit stralen met verschillende golflengten bestaat. Toegegeven, vergeleken met het licht dat door een LED wordt uitgezonden, heeft een laser een bijzonder smal spectrum. Vergelijk maar eens de golflengtespectra van een laser en een LED, die beide een piek hebben bij de golflengte λ0.

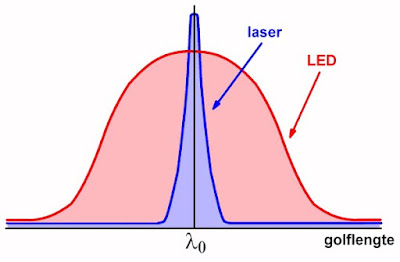Vergelijking van het spectrum van een laser en een LED.
(© 2023 Jos Verstraten)

De chromatische vervorming
Het licht van een laser in dus niet helemaal monochromatisch en het gevolg is dat een laserpuls, die in een glasvezel wordt gestuurd, in de vezel wordt verstrooid in functie van de tijd. De puls bestaat immers uit lichtstralen met allemaal iets verschillende golflengtes en door de chromatische dispersie zal de ene golflengte zich iets sneller door de glasvezel voortplanten dan de andere golflengtes. Er ontstaan als gevolg van deze eigenschap looptijdverschillen, die zich ook nu uiten door een vervorming van het signaal. Deze vervorming noemt men de 'chromatische vervorming' en het ontstaan daarvan wordt toegelicht aan de hand van de onderstaande figuur.

In deze figuur is één pulsje getekend dat in de glasvezel wordt gestuurd. Maar dit pulsje bestaat in feite uit een aantal deelpulsjes, die ieder een iets afwijkende golflengte hebben. Het gevolg van de chromatische dispersie is dat al deze pulsjes zich met een iets afwijkende snelheid door de glasvezel voortplanten en dus iets ten opzichte van elkaar vertraagd aan het einde van de vezel aankomen. De totale breedte van de puls neemt dus toe.
Het zal duidelijk zijn dat de chromatische vervorming toeneemt als de kabel langer is. Hoe langer de kabel, hoe meer looptijdverschillen er tussen de verschillende golflengtes zullen optreden en hoe breder de uitgangspuls wordt uitgesmeerd.

Het ontstaan van chromatische vervorming. (© 2023 Jos Verstraten)

De demping van een glasvezel
Een koperen geleider heeft een bepaalde soortelijke weerstand, die tot gevolg heeft dat een deel van de elektrische energie die door de geleider vloeit verloren gaat onder de vorm van warmte. Ook bij een glasvezel is een dergelijk verschijnsel bekend. De kern absorbeert en verstrooit een gedeelte van de lichtenergie, hetgeen uitgedrukt kan worden in een verlies of demping. Als eenheid van deze demping gebruikt men de dB/km. Deze demping is echter alles behalve een lineaire grootheid en verloopt zeer grillig. Kijk maar naar de onderstaande grafiek waarin de demping, uitgedrukt in dB/km, is uitgezet in functie van de golflengte van het licht. Dit vreemdsoortige verloop van de demping van een glasvezel wordt veroorzaakt door twee factoren: 
       - Moleculaire absorbtie.
       - Rayleigh verstrooiing.

De demping van een glasvezel in functie van de golflengte van het licht.
(© 2023 Jos Verstraten)

Moleculaire absorbtie
Moleculaire absorbtie wordt veroorzaakt door de aanwezigheid van negatief geladen OH-ionen in het materiaal van de vezel. Deze zogenaamde water-ionen zullen voornamelijk straling van bepaalde golflengtes absorberen, hetgeen zich uit in de aanwezigheid van een aantal sterkte dempingspieken. Deze pieken noemt men de 'OH-absorbtie'. Bij een glasvezel uit kwarts liggen deze pieken bij golflengten van 940 nm, 1.240 nm en 1.390 nm. Het zal duidelijk zijn dat deze pieken geminimaliseerd kunnen worden door de glasvezel uit zeer zuivere grondstoffen te vervaardigen. Maar helemaal weg gaan deze pieken nooit! Vooral de piek bij 1.390 nm is zeer hoog. Het gevolg van deze moleculaire absorbtie is dat men geen licht van gelijk welke golflengte kan gebruiken om de vezel aan te stralen. Het zal duidelijk zijn dat het onzin zou zijn om een lichtbron toe te passen die licht uitstraalt met een golflengte van ongeveer 1.400 nm. Het grootste gedeelte van de lichtenergie zou geabsorbeerd worden door de laatste waterpiek.

Rayleigh verstrooiing
Dit verschijnsel ontstaat door afwijkingen in de homogeniteit van het materiaal. Deze uiten zich als zeer plaatselijke variaties van de waarde van de brekingsindex. Het zal duidelijk zijn dat men ook deze demping kan minimaliseren door veel zorg te besteden aan het trekken van de vezel uit de grondstof. Maar er bestaat uiteraard een onderste grens aan het verbeteren van de homogeniteit van de vezel. Deze grens ligt bij verschillen in de materiaaldichtheid die in de grootte-orde van de golflengte van het licht liggen. Deze kan men, zelfs met de meest verfijnde productietechnieken, niet onder controle krijgen. Deze theoretische onderste grens aan de homogeniteit van het materiaal veroorzaakt de 'Rayleigh verstrooiing'. De demping die daarvan het gevolg is neemt exponentieel af in functie van de golflengte. Bij een golflengte van 1.550 nm bedraagt de Rayleigh-demping nog slechts 0,14 dB/km.

De vensters van een glasvezel
Uit de dempingsgrafiek van een glasvezel uit kwarts blijkt dat er drie gebieden zijn waar de demping minimaal is. Dit worden de 'vensters' van de glasvezel genoemd. Deze vensters liggen bij golflengten rond 850 nm, 1.300 nm en 1.550 nm. Het zal duidelijk zijn dat het bij de keuze van de lichtbron noodzakelijk is rekening te houden met deze vensters en men bij voorkeur een lichtbron selecteert die licht uitstraalt met een golflengte die in een van de vensters ligt. De drie vensters bevinden zich in het infrarode golflengte-spectrum en het zal dus duidelijk zijn dat de lichtbronnen infrarood licht moeten uitstralen.

De demping van kunststof vezels
Tot nu toe is altijd uitgegaan van glasvezels van kwarts. Er zijn echter ook kunststof vezels op de markt, die voornamelijk gebruikt worden voor optische communicatie over kleine afstanden, zoals bij computernetwerken in bedrijven. Deze vezels hebben totaal andere dempingskarakteristieken. Een typisch voorbeeld is getekend in de onderstaande figuur. De vensters bevinden zich hier bij 560 nm en bij 660 nm, dus in het zichtbare gedeelte van het lichtspectrum. Vandaar dat dit soort vezels vaak met gewone groene en rode LED's worden bestraald. Maar omdat infrarode LED's een hoger rendement hebben, werkt men bij deze vezels soms tóch met infrarode LED's met een golflengte van 850 nm. Zoals uit deze grafiek blijkt, hebben kunststof vezels een veel hogere demping dan kwarts vezels. Een polymeer kabel zoals de TX-CC1000-1A heeft een demping van 180 dB/km bij 650 nm. En dit wordt door de fabrikant een kabel met lage demping genoemd!

De demping van een kunststof vezel in functie van de golflengte van het licht.
(© 2023 Jos Verstraten)

De numerieke apertuur en de acceptatie-kegel
Een volgende belangrijke eigenschap van een glasvezel kabel is de zogenoemde 'numerieke apertuur', afgekort tot NA. De NA is gelijk aan de sinus van de maximale instralingshoek in de vezel, waarbij nog volledige reflectie optreedt. Een en ander wordt verduidelijkt aan de hand van de onderstaande figuur. In deze figuur is een lichtstraal getekend, die binnen valt onder een hoek α. Het gevolg is dat deze straal de scheiding tussen core en cladding onder een hoek β treft. Dit is de kritische hoek waarbij nog zo goed als volledige reflectie wordt gegarandeerd.
Wil de koppeling tussen lichtbron en glasvezel een zo hoog mogelijk rendement hebben, dan zullen alle uitgezonden lichtstralen binnen een kegel moeten vallen die ten opzichte van de lengterichting van de vezel een hoek heeft van +α tot -α. Deze instralingskegel noemt men de 'acceptatie-kegel' van de glasvezel.
Om de waarde van deze acceptatie-hoek α vast te leggen wordt gebruik gemaakt van het begrip numerieke apertuur. Een NA van 0,2 heeft een acceptatie-hoek van 12° tot gevolg. De acceptatie-kegel heeft dan uiteraard een hoek van 24°.

De 'numerieke apertuur' van een glasvezel kabel.
(© 2023 Jos Verstraten)

In het algemeen wordt gebruik gemaakt van een heel klein lensje, opgesteld tussen de lichtbron en de kern van de vezel. Dit lensje bundelt de uitgezonden lichtstralen zodanig, dat een zo groot mogelijk deel ervan binnen de acceptatie-kegel valt.
De numerieke apertuur is afhankelijk van het verschil in brekingsindex tussen het materiaal van de core en het materiaal van de cladding. De numerieke apertuur van de meeste glasvezels ligt tussen 0,1 en 0,4. Voor kunststof vezels gelden waarden voor NA tussen 0,3 en 0,5.

De transmissiesnelheid
Met de transmissiesnelheid wordt de hoeveelheid gegevens gedefinieerd die u per tijdseenheid door een glasvezel kabel kunt sturen. Het zal duidelijk zijn dat deze grootheid voor een belangrijk deel wordt bepaald door de twee dispersies van het gebruikte materiaal.
Maar daarnaast speelt ook de kwaliteit van de lichtbron een rol. Hoe beter deze lichtbron het ideaal van een monochromatische straler benadert, hoe minder chromatische dispersie er in de vezel optreedt en hoe groter de transmissiesnelheid zal zijn.

De bandbreedte
Een vertrouwd begrip uit de communicatie via koperen geleiders is 'bandbreedte'. De bandbreedte zegt bijna alles over de transportkwaliteit van een koperen kabel. Het zou derhalve handig zijn ook voor een glasvezel een begrip bandbreedte te definiëren. Maar dit gaat niet zo eenvoudig! Bij glasvezels speelt de lengte van de vezel een belangrijke rol. Hoe langer de kabel, hoe kleiner de bandbreedte en dit vanwege de genoemde dispersie-verschijnselen. Dit wordt toegelicht aan de hand van de onderstaande figuur. Links zijn twee pulsen getekend die vlak na elkaar door de lichtbron in de glasvezel worden gestraald. Deze twee pulsen planten zich voort door de vezel, maar door de reeds verklaarde dispersieverschijnselen zullen de pulsen steeds breder worden. Na een bepaalde afstand zijn de pulsen zo zeer verbreed dat zij niet meer als afzonderlijke impulsen te onderscheiden zijn, maar één brede puls met twee toppen vormen.

De invloed van de kabellengte op de bandbreedte. (© 2023 Jos Verstraten)

Vandaar dat men de bandbreedte bij glasvezel communicatie niet kan loskoppelen van de kabellengte. De eenheid van bandbreedte bij glasvezels is dus niet MHz, maar MHz.km. Deze grootheid geeft aan dat een kabel met een lengte van 1 km een bandbreedte heeft van x MHz. In de onderstaande figuur wordt dit toegelicht aan de hand van een voorbeeld. In de grafiek is de bandbreedte in afhankelijkheid van de vezellengte getekend voor een glasvezel die een bandbreedte heeft van 25 MHz.km. Hieruit blijkt dat de vezellengte een enorm grote invloed heeft op de bandbreedte. Reeds na 5 km is de reële bandbreedte van deze vezel teruggevallen tot minder dan 2 MHz.

Een voorbeeld van de bandbreedte definitie van een glasvezel kabel.
(© 2023 Jos Verstraten)

Soorten glasvezel kabels

Inleiding
Er zijn drie verschillende soorten glasvezel kabels ontwikkeld. Deze verschillen onderling in de manier waarop de core en de cladding zijn samengesteld. Deze drie soorten worden genoemd: 
       - De multimodus step-index kabel. 
       - De multimodus gradiënt kabel. 
       - De monomodus step-index kabel.
Zoals de namen reeds doen vermoeden hebben de onderlinge verschillen voornamelijk te maken met het aantal modi dat wordt toegestaan. Ofwel, met de hoeveelheid verschillende paden die de lichtstralen door de vezels kunnen volgen. De voornaamste verschillen tussen de drie soorten vezels zijn samengevat in de onderstaande figuur. 

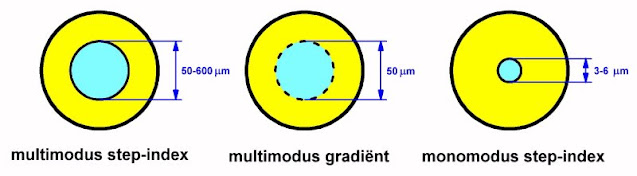De fundamentele verschillen tussen de drie soorten glasvezel kabels. (© 2023 Jos Verstraten) 

• De multimodus step-index kabel, links getekend, bestaat uit een vrij dikke kern met een dunne mantel eromheen. De lichtstralen hebben dus vele paden of modi om zich door de kabel voort te planten.
• De multimodus gradiënt kabel, getekend in het midden, heeft een kern van ongeveer 50 μm diameter met een dunne mantel. Het verschil tussen deze kabel en de eerst besproken is dat er geen abrupte overgang is tussen kern en mantel. Er is geen sprake van twee duidelijk gedefinieerde brekingsindexen, deze van de kern en deze van de mantel. Er wordt een vrij geleidelijke overgang tussen kern en mantel gerealiseerd, vandaar dat deze overgang met een gestippelde lijn is aangegeven.
• De monomodus step-index kabel, getekend in de rechter figuur, heeft een zeer dunne kern van 3 tot 6 μm en een dikke mantel. Het zal duidelijk zijn dat de lichtstralen nu erg weinig paden ter beschikking hebben om door de kabel te gaan. Vandaar de naam 'monomodus' of soms ook 'singlemodus'. 

De multimodus step-index kabel
De samenstelling van en het lichttransport door deze kabel is nog eens getekend in de onderstaande figuur. Links naast de doorsnede tekening staat een grafiekje dat het verloop van de brekingsindex aangeeft. Er bestaat een duidelijke stap in de brekingsindex, namelijk op het scheidingsvlak van kern en mantel. Vandaar de benaming 'step-index'.
De core is relatief dik, tussen 50 en 600 μm, en vandaar is deze kabel tamelijk eenvoudig en goedkoop te maken. Deze verscheen dan ook als eerste op de markt. Bovendien is het, vanwege de dikte van de core, vrij eenvoudig mogelijk om deze kabels aan elkaar te koppelen of het einde van de kabel te focusseren op de zender en de ontvanger, hetgeen nog eens een belangrijke kostenreductie met zich mee brengt.
Het grootste nadeel van deze kabel volgt uit het rechter tekeningetje. Omdat de kern dik is, kan het licht zich via zeer vele paden of modi door de kabel voortplanten. Met als gevolg grote dispersie-vervormingen door de looptijdverschillen in de kern. De bandbreedte van dit soort kabels is dan ook tamelijk beperkt. De multimodus step-index kabel wordt dan ook voornamelijk gebruikt voor het overbruggen van kleine afstanden, waarbij lage transmissiesnelheden worden toegepast. Deze kabels zijn bijvoorbeeld ideaal voor het realiseren van optisch gekoppelde computernetwerken in kleine kantoorgebouwen.
Een overzicht van de belangrijkste specificaties van de multimodus step-index kabels: 
       - Kerndiameter: 50 tot 600 μm
       - Bandbreedte: 10 tot 100 MHz.km
       - Brekingsindex n1 kern: ongeveer 1,50
       - Brekingsindex mantel: 0,96 ● n1
       - Numerieke apertuur: 0,2 tot 0,7
       - Demping: 5 tot 30 dB/km
       - Dispersie: 10 tot 100 ns/km

De karakteristieken van de multimodus step-index kabel. (© 2023 Jos Verstraten) 

De multimodus gradiënt kabel
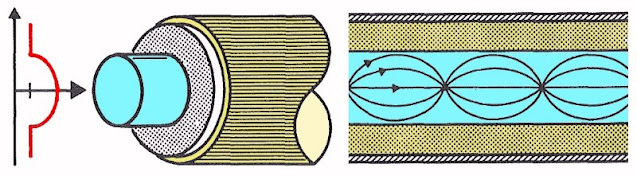
Zoals uit de onderstaande figuur blijkt, verschilt deze kabel alleen in het verloop van de brekingsindex van de multimodus step-index kabel. Er is nu geen sprake van een plotselinge overgang op het grensgebied tussen core en cladding, maar van een geleidelijke overgang. Men zou kunnen zeggen dat core en cladding min of meer in elkaar versmolten zijn.
Wat zijn de gevolgen? Het zal duidelijk zijn dat de lichtstralen zich nu niet meer via rechtlijnige paden door de kabel kunnen voortplanten. Door het graduele verloop van de brekingsindex zullen de paden min of meer sinusvormig verlopen, zoals getekend in de figuur. Het zal duidelijk zijn dat het verschil in looptijd tussen de kortste weg en de langste weg nu veel kleiner is dan bij de step-index kabel. De vervormingen onder invloed van looptijdverschillen zijn dus kleiner, met als rechtstreeks gevolg een veel grotere bandbreedte en een grotere transmissiesnelheid. Bovendien kunnen er langere afstanden mee worden gerealiseerd.
De fabricage van de multimodus gradiënt kabel is iets ingewikkelder dan deze van de step-index kabel. De prijs is dus hoger, maar dit weegt niet op tegen de veel betere specificaties van dit soort kabels. 

Kijk maar eens naar onderstaande samenvatting en vergelijk deze met dezelfde specificaties van de step-index kabel: 
       - Kerndiameter: 50 tot 150 μm
       - Bandbreedte: 200 tot 1.500 MHz.km
       - Brekingsindex n1 kern: ongeveer 1,50
       - Brekingsindex mantel: 0,99 ● n1
       - Numerieke apertuur: 0,14 tot 0,25

       - Demping: 3 tot 10 dB/km 
       - Dispersie: 1 tot 5 ns/km

De karakteristieken van de multimodus gradiënt kabel. (© 2023 Jos Verstraten)

De monomodus step-index kabel
Het is duidelijk dat de diameter van de core een grote rol speelt bij de kwalitatieve eigenschappen van een glasvezel kabel. Hoe dunner de core, hoe minder modi het licht heeft om zich door de kabel voort te planten en hoe minder looptijdverschillen er ontstaan. Ideaal zou natuurlijk een kabel zijn waar er maar één modus is: die waarbij het licht zich alleen in de lengte-as van de vezel kan voortplanten. Er ontstaan dan helemaal geen looptijdverschillen, met als gevolg dat u geweldige bandbreedtes mag verwachten.

Hoe dik zou de core van een dergelijke ideale glasvezel moeten zijn? Het valt, ook zonder ingewikkelde fysica, wel zonder meer aan te nemen dat deze ideale situatie zich voordoet als de diameter van de kern gelijk is aan de golflengte van het licht. Nu ligt de gebruikte golflengte van het licht, zoals ondertussen bekend, tussen 800 en 1.600 nm. Omgerekend naar de schaal waarin men de diameter van glasvezels meet komt dit dus overeen met diameters tussen 0,8 en 1,6 μm, minder dan één duizendste millimeter!
Het zal duidelijk zijn dat het fabriceren van een glasvezel met een kern die dunner is dan de geleidende sporen in een IC geen sinecure is. Bovendien wordt het dan natuurlijk heel problematisch om kabels aan elkaar te bevestigen. De minste of geringste afwijking in de positie van beide kernen heeft tot gevolg dat de kernen niet meer in elkaars verlengde liggen en de kabel zichzelf volledig blokkeert voor het geleiden van licht. In de praktijk werkt men (nog) niet met echt golflengte-dunne vezels, maar men komt met diameters van 3 μm aardig in de buurt!
Een samenvatting van de belangrijkste specificaties van monomodus step-index kabels:
       - Kerndiameter: 3 tot 6 μm
       - Bandbreedte: 10.000 tot 50.000 MHz.km
       - Brekingsindex kern n1: ongeveer 1,50
       - Brekingsindex mantel: 0,995 ● n1
       - Numerieke apertuur: 0,09 tot 0,1
       - Demping: 2 tot 5 dB/km
       - Dispersie: 0,000.1 ns/km

De karakteristieken van de monomodus step-index kabel. (© 2023 Jos Verstraten)

Glasvezel kabels in de praktijk

Afwerking van de vezels
De besproken vezels zijn nu weliswaar klaar om lichtsignalen te geleiden, maar nog veel te dun om praktisch bruikbaar te zijn. Vandaar dat er nog diverse lagen worden aangebracht die als voornaamste taak hebben de vezel praktisch manipuleerbaar te maken. Een vaak toegepaste afwerking is geschetst in de onderstaande figuur. Over de jacket wordt een siliconenvulling aangebracht, die wordt afgewerkt met een binnenmantel en een vezellaag, die tot taak heeft de trekkrachten die op de vezel worden uitgeoefend op te vangen. Nadien volgt nog een kunststof buitenmantel.

De standaard afwerking van een één-aderige kabel. (© 2023 Jos Verstraten)

Meeraderige kabels
In de meeste gevallen worden de enkelvoudige aders gebundeld tot meeraderige kabels. In één kabel kunnen wel zo'n tweehonderd individuele vezels worden ondergebracht. Uiteraard zijn de variaties op dit gebied eindeloos. Zo worden ook samengestelde kabels gefabriceerd waarin, naast honderden glasvezel aders ook nog eens traditionele koperen aders zijn verwerkt. 

Een samengestelde kabel. (© Connectivity Solutions)

Soorten leverbare glasvezel kabels
Er worden uiteraard verschillende soorten glasvezel kabels gefabriceerd. De eerste manier van onderscheiden is het verschil tussen multimodus en monomodus kabels. Deze twee categorieën zijn echter weer opgedeeld in een aantal subcategorieën.
Monomodus kabels worden aangeboden als OS1 en OS2, multimodus als OM1, OM2, OM3, OM4 en OM5. Multimodus wordt vooral gebruikt voor kleinere afstanden tot maximaal 2 km. Met monomodus is het mogelijk om afstanden tot wel 40.000 km te overbruggen. Multimodus wordt veel meer gebruikt dan monomodus en beslaat ongeveer 90 % van de markt.
Monomodus kabels zijn te herkennen aan hun gele kleur. Multimodus kabels kunnen diverse kleuren hebben, afhankelijk of het OM1, OM2, OM3, OM4 of OM5 is. OM1 en OM2 zijn beiden oranje, OM3 is aqua, OM4 is erika violet (een beetje de kleur van heideplanten) en OM5 is lime green.
Tot slot een kort overzicht van de eigenschappen van die diverse codes:

• OM1
  Kern/manteldiameters 62,5/125 µm, kleurcode oranje, typisch voor led-toepassingen.
• OM2
  Kern/manteldiameters 50/125 µm, kleurcode oranje, typisch voor led-toepassingen.
• OM3
  Kern/manteldiameters 50/125 µm, kleurcode aqua, voor hogesnelheidstoepassingen zoals 10/40/100 Gigabit Ethernet of Fibre Channel.
• OM4
  Kern/manteldiameters 50/125 µm, kleurcode violet, voor hogesnelheidstoepassingen zoals 10/40/100 Gigabit Ethernet of Fibre Channel.
• OM5
  Kern/manteldiameters 50/125 µm, kleurcode lime, voor hogesnelheidstoepassingen zoals 10/40/100 Gigabit Ethernet of Fibre Channel.
• OS1
  Kern/mantel diameters 9/125 µm, kleurcode geel, voor het overbruggen van grote afstanden en voor hoge bandbreedtes.
• OS2
  Kern-/manteldiameters 9/125 µm, kleurcode geel, voor het overbruggen van grote afstanden en voor hoge bandbreedtes.

(Banggood sponsor advertentie)
FG-100 DDS Function generator