Inleidende begrippen
Wat ontdekte Fourier?
Jean-Baptiste Joseph Fourier was een Franse wis- en natuurkundige, geboren in 1768. Hij is vooral bekend geworden door de fourier-analyse en de fourier-transformatie, die naar hem zijn vernoemd.
Als u naar een muziektoon van een bepaalde frequentie luistert door bijvoorbeeld een snaar van een viool te laten trillen, dan valt het onmiddellijk op dat die toon heel anders kan klinken als hij op een ander instrument wordt gespeeld. Hoe kan dat? Het blijkt dat die toon niet alleen wordt geproduceerd door snaartrillingen op de basisfrequentie, maar dat de klankkleur voornamelijk wordt bepaald door de aanwezigheid van de zogenaamde boventonen. Dat zijn trillingen die frequenties hebben die een veelvoud zijn van de frequentie van de grondtoon. Deze trillingen worden de 'harmonischen' genoemd. De verhoudingen tussen het volume van de basisfrequentie en het volume van de harmonischen is er verantwoordelijk voor hoe een toon van een bepaald instrument klinkt.
U zou deze volumeverhouding als het ware het DNA-profiel van het instrument kunnen noemen.
Fourier bewees, op een wiskundig heel ingewikkelde manier, dat ieder periodiek signaal is samengesteld uit een sinusvormig of cosinusvormig signaal met een basisfrequentie en een heleboel van die harmonischen. En net zoals die samenstelling de toon van een muziekinstrument bepaalt, bepaalt die samenstelling ook de vorm van het periodiek signaal. Die onderlinge verhouding tussen de groottes van de basisfrequentie en de harmonischen wordt de 'fourier-reeks' van het signaal genoemd.
Fourier betekent héél véél wiskunde
Als u, als wiskundig niet geschoolde, wel eens hebt gezocht op het internet naar een verhaal over fourier, fourieranalyse of fourier-reeksen, dan kwam u ongetwijfeld terecht op dergelijke pagina's:
Dat is een stuk uit het artikel op Wikipedia over het trefwoord 'fourier-reeks'. Niet erg uitnodigend om te gaan lezen, laat staan begrijpen! Vandaar dat wij een poging gaan wagen dit belangrijke begrip uit de elektronica op een niet-wiskundige manier te verklaren. Dat de wiskundig geschoolde lezer(es) bij het lezen van dit artikel af en toe de haren ten berge voelt rijzen nemen wij dan maar op de koop toe.
Wat is een periodiek signaal?
Dat is een signaal dat zich in het verloop van de tijd op een volledig identieke manier voortdurend herhaalt.
Wat is een sinus spanning?
De sinus spanning, voorgesteld in de onderstaande figuur, is de zuiverste vorm van een periodiek signaal. Zo'n spanning wordt gedefinieerd door een periode en door een amplitude. De periode is de tijdsduur van één trilling van het signaal. De amplitude is de maximale grootte die het signaal binnen zo'n periode bereikt.
In de figuur zijn dus drie perioden voorgesteld. De periode is een tijdsduur en wordt uitgedrukt in seconden, milliseconden of microseconden. In de praktijk wordt de periode van een sinus echter omgerekend naar de frequentie f. Die grootheid geeft het aantal perioden per seconde. Als één periode 1 ms duurt, dan gaan er 1.000 perioden in één seconde en bedraagt de frequentie f van het signaal 1.000 Hz of 1 kHz.
De amplitude is een spanning en wordt uitgedrukt in volt.
Het kenmerkende van een sinus spanning is dat de grootte van de spanning bij het begin van de periode altijd nul is. Nadien stijgt de spanning tot de maximale waarde (de amplitude) en daalt weer tot de spanning in exact de helft van de periode weer nul wordt. Vervolgens wordt deze cyclus herhaald, maar nu met negatieve waarden van de spanning.
Hoe ontstaat de typische vorm van een sinus spanning?
Daar is veel wiskundigs over te schrijven, maar wij beperken ons tot de onderstaande animated gif. Als u onder een spoel een magneet laat draaien dan zal het meedraaiend magnetisch veld een spanning opwekken in die spoel. En die spanning is, inderdaad, een sinusoidaal verlopende spanning. Als de magneet één omwenteling maakt zal in de spoel één periode van de sinus spanning worden gegenereerd.
U zou deze volumeverhouding als het ware het DNA-profiel van het instrument kunnen noemen.
Fourier bewees, op een wiskundig heel ingewikkelde manier, dat ieder periodiek signaal is samengesteld uit een sinusvormig of cosinusvormig signaal met een basisfrequentie en een heleboel van die harmonischen. En net zoals die samenstelling de toon van een muziekinstrument bepaalt, bepaalt die samenstelling ook de vorm van het periodiek signaal. Die onderlinge verhouding tussen de groottes van de basisfrequentie en de harmonischen wordt de 'fourier-reeks' van het signaal genoemd.
Fourier betekent héél véél wiskunde
Als u, als wiskundig niet geschoolde, wel eens hebt gezocht op het internet naar een verhaal over fourier, fourieranalyse of fourier-reeksen, dan kwam u ongetwijfeld terecht op dergelijke pagina's:
 |
| Zo wordt het begrip 'fourier-reeks' op Wikipedia besproken. |
Dat is een stuk uit het artikel op Wikipedia over het trefwoord 'fourier-reeks'. Niet erg uitnodigend om te gaan lezen, laat staan begrijpen! Vandaar dat wij een poging gaan wagen dit belangrijke begrip uit de elektronica op een niet-wiskundige manier te verklaren. Dat de wiskundig geschoolde lezer(es) bij het lezen van dit artikel af en toe de haren ten berge voelt rijzen nemen wij dan maar op de koop toe.
Wat is een periodiek signaal?
Dat is een signaal dat zich in het verloop van de tijd op een volledig identieke manier voortdurend herhaalt.
Wat is een sinus spanning?
De sinus spanning, voorgesteld in de onderstaande figuur, is de zuiverste vorm van een periodiek signaal. Zo'n spanning wordt gedefinieerd door een periode en door een amplitude. De periode is de tijdsduur van één trilling van het signaal. De amplitude is de maximale grootte die het signaal binnen zo'n periode bereikt.
In de figuur zijn dus drie perioden voorgesteld. De periode is een tijdsduur en wordt uitgedrukt in seconden, milliseconden of microseconden. In de praktijk wordt de periode van een sinus echter omgerekend naar de frequentie f. Die grootheid geeft het aantal perioden per seconde. Als één periode 1 ms duurt, dan gaan er 1.000 perioden in één seconde en bedraagt de frequentie f van het signaal 1.000 Hz of 1 kHz.
De amplitude is een spanning en wordt uitgedrukt in volt.
Het kenmerkende van een sinus spanning is dat de grootte van de spanning bij het begin van de periode altijd nul is. Nadien stijgt de spanning tot de maximale waarde (de amplitude) en daalt weer tot de spanning in exact de helft van de periode weer nul wordt. Vervolgens wordt deze cyclus herhaald, maar nu met negatieve waarden van de spanning.
 |
| Voorstelling van drie perioden van een sinus spanning. (© 2021 Jos Verstraten) |
Hoe ontstaat de typische vorm van een sinus spanning?
Daar is veel wiskundigs over te schrijven, maar wij beperken ons tot de onderstaande animated gif. Als u onder een spoel een magneet laat draaien dan zal het meedraaiend magnetisch veld een spanning opwekken in die spoel. En die spanning is, inderdaad, een sinusoidaal verlopende spanning. Als de magneet één omwenteling maakt zal in de spoel één periode van de sinus spanning worden gegenereerd.
 |
Het ontstaan van een sinus spanning. (© Ungenergi) |
Wat is een cosinus spanning?
Een dergelijke spanning is voorgesteld in de onderstaande figuur en lijkt dus als twee druppels water op een sinus spanning. Er is echter één groot verschil. Bij het begin van de periode is de cosinus spanning maximaal, dus gelijk aan de amplitude. Nadien evolueert de spanning naar nul, wordt negatief, wordt weer nul en eindigt weer op de maximale waarde.
 |
| Eén periode van een cosinus spanning. (© 2021 Jos Verstraten) |
Een horizontale as in hoekgraden
In de vorige figuren is de horizontale as ingedeeld in tijden. Op die manier kunt u van die as de periodeduur van de sinus of cosinus spanning aflezen en daaruit de frequentie van het signaal berekenen.
Vaak ziet u op de horizontale as echter een indeling in graden (°). Een periode van het signaal bestaat dan uit 360°. Dat heeft te maken met de in de bovenstaande figuur voorgestelde manier waarop de sinus ontstaat. Een volledige omwenteling van de magneet kan ingedeeld worden in 360° (hoekgraden) en voor iedere hoekverdraaiing van de magneet kunt u in de grafiek de overeenkomende waarde van de spanning intekenen.
In de onderstaande grafiek zijn een sinus en een cosinus spanning in één grafiek getekend. De horizontale as is ingedeeld in graden. U ziet dat er een verschil van 90° bestaat tussen de sinus en de cosinus. Men noemt dat meestal het 'faseverschil' of de 'fasehoek'.
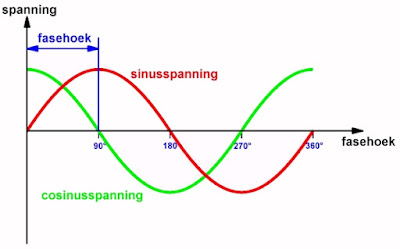 |
| Tussen de sinus en de cosinus bestaat een faseverschil van 90°. (© 2021 Jos Verstraten) |
Sinus en cosinus spanningen in formulevorm
Wiskundig gezien is het geen enkel probleem om beide spanningen onder de vorm van een formule te schrijven. Maar wij beloofden in dit artikel geen wiskunde te gebruiken. Dus hebben wij een eigen manier verzonnen om deze twee fundamentele spanningsvormen der elektrotechniek weer te geven:
signaal = amplitude • sin(frequentie)
en
signaal = amplitude • cos(frequentie)
In die weergave zitten de amplitude, de frequentie en de signaalvorm. Zij definieert dus het signaal volledig, meer hoeft u over dat signaal niet te weten om het te kunnen voorstellen.
In de onderstaande figuur zijn een sinus en een cosinus voorgesteld met een frequentie van respectievelijk 1 kHz en 2 kHz en met amplituden van respectievelijk 1 V en 0,5 V. In onze notatie worden deze signalen dus voorgesteld door:
signaal(1) = 1 V • sin(1 kHz)
en
signaal(2) = 0,5 V • cos(2 kHz)
 |
| De grafische weergave van beide signalen. (© 2021 Jos Verstraten) |
Het optellen van sinus en cosinus spanningen
Een elektronische optelschakeling
In gedachten kunt u zich ongetwijfeld de onderstaande schakeling voorstellen. Op een aantal ingangen kunt u met elkaar gesynchroniseerde sinus en cosinus spanningen aanleggen. Dat 'gesynchroniseerd' wil zeggen dat de frequenties van al die signalen exacte veelvouden zijn van de frequentie van signaal(1) en dat bovendien alle signalen op precies hetzelfde moment in de tijd zijn gestart op nul (sinus) of op de maximale waarde (cosinus). Door middel van potentiometers R1 tot en met R5 kunt u de grootte van die signalen instellen tussen 0 V en 1 V. De lopers gaan naar een schakeling MENGER waarin al die signalen bij elkaar worden opgeteld. Op de uitgang van die schakeling staat het signaal(uitgang) ter beschikking.
 |
| Een schakeling waarmee u sinus en cosinus spanningen bij elkaar kunt optellen. (© 2021 Jos Verstraten) |
Een voorbeeldje
Stel dat u twee signalen aan de schakeling aanbiedt:
signaal(1) = 0,7 V • sin(1 kHz)
en
signaal(2) = 0,3 V • cos(10 kHz)
Uit de mengschakeling komt dan een signaal:
signaal(uitgang) = signaal(1) + signaal(2)
signaal(uitgang) = [0,7 V • sin(1 kHz)] + [0,3 V • cos(10 kHz)]
In de onderstaande figuur wordt deze optelling van beide signalen grafisch voorgesteld en ziet u meteen hoe zo'n samengesteld signaal er uit komt te zien.
 |
| Het optellen van twee signalen. (© 2021 Jos Verstraten) |
Vereenvoudigingen
U kunt de door ons verzonnen 'formule' nog wat vereenvoudigen. U kunt de frequentie van 1 kHz gewoon voorstellen door het symbool 'f'. Dan wordt de frequentie van 10 kHz uiteraard voorgesteld door het symbool '10f'.
De 'formule' van het uitgangssignaal wordt dan:
signaal(uitgang) = [0,7 V • sin(f)] + [0,3 V • cos(10f)]
Verder kunt u een spanning van 1 V ook voorstellen door '1,0' en dan worden spanningen van 0,3 V en 0,7 V uiteraard '0,3' en '0,7'. Onze 'formule' wordt dan nog meer vereenvoudigd tot:
signaal(uitgang) = [0,7 • sin(f)] + [0,3 • cos(10f)]

De eerste fourier-reeks!
Met dit eenvoudige voorbeeld hebben wij u kennis laten maken met de eerste fourier-reeks uit dit artikel. De fourier-reeks:
signaal(uitgang) = [0,7 • sin(f)] + [0,3 • cos(10f)]
beschrijft het uitgangssignaal van het bovenstaande voorbeeld volledig. Meer gegevens hebt u niet nodig om dat signaal te reconstrueren.
De fourier-reeks van een zaagtand spanning
Inleiding
U weet hoe een zaagtand spanning er uit ziet. Het is moeilijk te bevatten dat een dergelijk signaal, voorgesteld in de onderstaande figuur, gevormd kan worden door uitsluitend sinus en cosinus spanningen met elkaar te mengen. Toch is het zo en dat gaan wij stap na stap aantonen.
 |
| Deze zaagtand gaan wij met behulp van de theorie van Fourier opbouwen. (© 2021 Jos Verstraten) |
Stap 1: het basissignaal
Wij beginnen met de fundamentele sinus. Stel dat u een zaagtand met een frequentie van 1 kHz nodig hebt. De basis van onze fourier-synthese is dan een sinus spanning met een amplitude van 1 V en een frequentie van 1 kHz. Zoals nu bekend wordt verondersteld kunnen wij dit signaal, dat meteen het uitgangssignaal van onze menger is, voorstellen als:
signaal(zaagtand-1) = [1,0 • sin(f)]
 |
| Het basissignaal voor het componeren van een zaagtand. (© 2021 Jos Verstraten) |
Stap 2: toevoegen van de tweede harmonische
In feite is dat de eerste harmonische, maar omdat dit signaal de dubbele frequentie heeft van het basissignaal noemt men dit toch de tweede harmonische. Uit de wiskundige theorie van de fourier-synthese kan men berekenen dat deze tweede harmonische (2 kHz) een amplitude van 0,5 V moet hebben en een sinusvormig verloop:
signaal(zaagtand-2) = [1,0 • sin(f)] + [0,5 • sin(2f)]
Het resultaat ziet u links op de eerstvolgende illustratie.
Stap 3: toevoegen van de derde harmonische
Fourier beweert dat de derde harmonische (3 kHz) een sinus is met een amplitude van 0,333 V:
signaal(zaagtand-3) = [1,0 • sin(f)] + [0,5 • sin(2f)] + [0,333 • sin(3f)]
Het resultaat ziet u in het midden op de eerstvolgende illustratie.
Stap 4: toevoegen van de vierde harmonische
Men kan berekenen dat de vierde harmonische (4 kHz) een amplitude van 0,25 V moet hebben en alweer een sinus is:
signaal(zaagtand-4) = [1,0 • sin(f)] + [0,5 • sin(2f)] + [0,333 • sin(3f)] + [0,25 • sin(4f)]
Het resultaat ziet u in rechts op de eerstvolgende illustratie.
 |
| Het toevoegen van de eerste drie harmonischen. (© 2021 Jos Verstraten) |
Stap 5: de hogere harmonischen mengen
Op dezelfde manier kunt u nu, door aan de potentiometers van de virtuele menger te draaien, de hogere harmonischen bij het uitgangssignaal mengen:
- Vijfde harmonische: + [0,2 • sin(5f)]
- Zesde harmonische: + [0,167 • sin(6f)]
- Zevende harmonische: + [0,143 • sin(7f)]
- Achtste harmonische: + [0,125 • sin(8f)]
- Negende harmonische: + [0,111 • sin(9f)]
- Tiende harmonische: + [0,1 • sin(10f)]
Die harmonischen zijn dus allemaal sinussen. De resultaten zijn, stap na stap, voorgesteld in de onderstaande figuur.
 |
| Het toevoegen van de hogere harmonischen. (© 2021 Jos Verstraten) |
De fourier-reeks van een zaagtand spanning
De fourier-reeks van een zaagtand tot en met de tiende harmonische kan dus worden geschreven als:
signaal(zaagtand-10) = [1,0 • sin(f)] + [0,5 • sin(2f)] + [0,333 • sin(3f)] + [0,25 • sin(4f)] + [0,2 • sin(5f)] + [0,167 • sin(6f)] + [0,143 • sin(7f)] + [0,125 • sin(8f)] + [0,111 • sin(9f)] + [0,1 • sin(10f)]
Besluiten
Uit de figuren en onze 'formule' kunt u een aantal conclusies trekken.
Uit de oscillogrammen blijkt duidelijk dat er meer dan tien harmonischen nodig zijn om het gecomponeerde signaal écht op een zaagtand te laten lijken. In de meeste gevallen stelt men dat er twintig harmonischen nodig zijn voor een goed lijkende fourier-synthese.
Een zaagtand bestaat uit uitsluitend sinusvormige harmonischen.
Uit onze 'formule' blijkt dat het amplitude-aandeel van de harmonischen steeds kleiner wordt.
De reeks der coëfficiënten
Als u de tien amplitude-getallen (men noemt dat de 'coëfficiënten') van de harmonischen goed bekijkt stelt u vast dat u deze ook kunt schrijven als de onderstaande reeks:
0,5 = 1/2
0,333 = 1/3
0,25 = 1/4
0,2 = 1/5
0,167 = 1/6
0,143 = 1/7
0,125 = 1/8
0,111 = 1/9
0,1 = 1/10
Uit deze reeks kunt u gemakkelijk afleiden hoe de coëfficiënten van de hogere harmonischen gaan verlopen: 1/11, 1/12, 1/13, etc.
Tijd domein? Dat kent u al!
Iedere elektronicus bekijkt signalen op een oscilloscoop. Zo'n oscillogram is in feite een grafiek die horizontaal een tijd weergeeft en verticaal een spanning. Het werken met zo'n voorstelling van een signaal noemt met 'werken in het tijd domein'. Die naam heeft natuurlijk alles te maken met de indeling van de horizontale as.

Werken in het frequentie domein
Dankzij de theorie van Fourier kunt u echter een periodiek signaal op een geheel andere manier voorstellen, die het signaal ook volledig beschrijft. In de onderstaande figuur is een grafiek getekend die een verticale spanning-as en een horizontale frequentie-as heeft. Verticaal zijn er twee schaalindelingen, eentje naar boven voor de harmonischen die een sinusvorm hebben en eentje naar onder voor de harmonischen die een cosinusvorm hebben.
In deze grafiek zet u alle coëfficiënten van de basisfrequentie en de harmonischen uit, waarbij u er op moet letten dat sinussen in de bovenste helft van de grafiek thuis horen en cosinussen in de onderste helft. Omdat de behandelde zaagtand-reeks alleen sinus-harmonischen heeft blijft in dit voorbeeld de onderste helft van de grafiek leeg. Het werken met deze voorstelling van een signaal noemt men 'werken in het frequentie domein'.
Tijd en frequentie domeinen in één figuur
Uit de onderstaande figuur kunt u aan de hand van een eenvoudig voorbeeldje duidelijk de verschillende benaderingen afleiden van werken in het tijd domein en werken in het frequentie domein. In het tijd domein meet u signalen met een oscilloscoop, in het frequentie domein meet u signalen met een spectroscoop.
FFT, Fast Fourier Transform
Vrijwel alle moderne digitale oscilloscopen hebben een optie die 'FFT' heet, het letterwoord van 'Fast Fourier Transform'. Dat is een software-algoritme waarmee men uit de gedigitaliseerde samples van het ingangssignaal van een oscilloscoop de fourier-reeks kan berekenen en deze op het scherm kan zetten. Met deze optie gaat uw oscilloscoop dus met één druk op de knop van het tijd domein naar het frequentie domein.
Nu moet u zich hiervan bij goedkope apparaten niet erg veel voorstellen. Alleen de écht professionele scopes van meer dan duizend euro zetten een fourier-reeks op het scherm waar u echt wat aan hebt. Ter illustratie ziet u in de onderstaande afbeelding het schermbeeld na de optie 'FFT' op onze middenklasse oscilloscoop XDS2102A van OWON. De gele trace geeft het tijd domein weer, de paarse het frequentie domein van een periodieke smalle puls.
De coëfficiënten van de harmonischen
Men kan berekenen dat de fourier-reeks van een blokgolf uit de onderstaande termen bestaat:
- Eerste harmonische: [1,0 • sin(f)]
- Derde harmonische: [0,333 • sin(3f)]
- Vijfde harmonische: [0,2 • sin(5f)]
- Zevende harmonische: [0,143 • sin(7f)]
- Negende harmonische: [0,111 • sin(9f)]
- Elfde harmonische: [0,091 • sin(11f)]
Bij deze signaalvorm spelen dus alleen de oneven harmonischen een rol. Let u er bovendien even op dat de coëfficiënten van deze harmonischen precies gelijk zijn aan deze van de reeds behandelde zaagtand. Wonderbaarlijk!
Het tijd domein van een blokgolf
In de onderstaande figuur hebben wij weer sinussen met de juiste amplitude en de juiste frequentie een na een aan onze imaginaire menger aangeboden en iedere keer het resultaat op onze oscilloscoop bekeken.
Het frequentie domein van een blokgolf
U kunt het grafiekje van het frequentie domein uit dat van de zaagtand afleiden door de even harmonischen te verwijderen.
Inleiding
In de onderstaande figuur ziet u een puls met een duty-cycle van 10 %. Dat betekent dat gedurende 10% van de periode de spanning hoog is en gedurende de overige 90% de spanning laag is. Zou zo'n periodieke puls ook met sinussen en cosinussen gemaakt kunnen worden? Laten wij het proberen!
De coëfficiënten van de harmonischen
Men kan berekenen dat de fourier-reeks van een dergelijke smalle periodieke puls uit de onderstaande termen bestaat:
- Eerste harmonische: [1,0 • sin(f)]
- Tweede harmonische: [0,9 • cos(2f)]
- Derde harmonische: [0,8 • sin(3f)]
- Vierde harmonische: [0,7 • cos(4f)]
- Vijfde harmonische: [0,6 • sin(5f)]
- Zesde harmonische: [0,5 • cos(6f)]
- Zevende harmonische: [0,4 • sin(7f)]
- Achtste harmonische: [0,3 • cos(8f)]
- Negende harmonische: [0,2 • sin(9f)]
- Tiende harmonische: [0,1 • cos(10f)]
Het rekenkundig verband tussen de coëfficiënten is, als u er even over filosofeert, toch wel wonderlijk te noemen! Merk op dat bij deze fourier-reeks ook cosinus-signalen betrokken zijn.
Het tijd domein van een periodieke smalle puls
In de onderstaande figuur hebben wij weer sinussen en cosinussen met de juiste amplitude en de juiste frequentie een na een aan onze imaginaire menger aangeboden en iedere keer het resultaat op onze oscilloscoop bekeken.
Het frequentie domein van een periodieke smalle puls
In de onderstaande grafiek ziet u hoe een dergelijke smalle periodieke puls in het frequentie domein voorgesteld wordt.
(Amazon sponsor advertentie)
Koop uw UPS bij Amazon

Als u de tien amplitude-getallen (men noemt dat de 'coëfficiënten') van de harmonischen goed bekijkt stelt u vast dat u deze ook kunt schrijven als de onderstaande reeks:
0,5 = 1/2
0,333 = 1/3
0,25 = 1/4
0,2 = 1/5
0,167 = 1/6
0,143 = 1/7
0,125 = 1/8
0,111 = 1/9
0,1 = 1/10
Uit deze reeks kunt u gemakkelijk afleiden hoe de coëfficiënten van de hogere harmonischen gaan verlopen: 1/11, 1/12, 1/13, etc.
Tijd domein versus frequentie domein
Tijd domein? Dat kent u al!
Iedere elektronicus bekijkt signalen op een oscilloscoop. Zo'n oscillogram is in feite een grafiek die horizontaal een tijd weergeeft en verticaal een spanning. Het werken met zo'n voorstelling van een signaal noemt met 'werken in het tijd domein'. Die naam heeft natuurlijk alles te maken met de indeling van de horizontale as.

Werken in het frequentie domein
Dankzij de theorie van Fourier kunt u echter een periodiek signaal op een geheel andere manier voorstellen, die het signaal ook volledig beschrijft. In de onderstaande figuur is een grafiek getekend die een verticale spanning-as en een horizontale frequentie-as heeft. Verticaal zijn er twee schaalindelingen, eentje naar boven voor de harmonischen die een sinusvorm hebben en eentje naar onder voor de harmonischen die een cosinusvorm hebben.
In deze grafiek zet u alle coëfficiënten van de basisfrequentie en de harmonischen uit, waarbij u er op moet letten dat sinussen in de bovenste helft van de grafiek thuis horen en cosinussen in de onderste helft. Omdat de behandelde zaagtand-reeks alleen sinus-harmonischen heeft blijft in dit voorbeeld de onderste helft van de grafiek leeg. Het werken met deze voorstelling van een signaal noemt men 'werken in het frequentie domein'.
 |
| Het weergeven van een zaagtand spanning in het frequentie domein. (© 2021 Jos Verstraten) |
Tijd en frequentie domeinen in één figuur
Uit de onderstaande figuur kunt u aan de hand van een eenvoudig voorbeeldje duidelijk de verschillende benaderingen afleiden van werken in het tijd domein en werken in het frequentie domein. In het tijd domein meet u signalen met een oscilloscoop, in het frequentie domein meet u signalen met een spectroscoop.
 |
| Het verschil tussen het tijd en het frequentie domein. (© 2021 Jos Verstraten) |
FFT, Fast Fourier Transform
Vrijwel alle moderne digitale oscilloscopen hebben een optie die 'FFT' heet, het letterwoord van 'Fast Fourier Transform'. Dat is een software-algoritme waarmee men uit de gedigitaliseerde samples van het ingangssignaal van een oscilloscoop de fourier-reeks kan berekenen en deze op het scherm kan zetten. Met deze optie gaat uw oscilloscoop dus met één druk op de knop van het tijd domein naar het frequentie domein.
Nu moet u zich hiervan bij goedkope apparaten niet erg veel voorstellen. Alleen de écht professionele scopes van meer dan duizend euro zetten een fourier-reeks op het scherm waar u echt wat aan hebt. Ter illustratie ziet u in de onderstaande afbeelding het schermbeeld na de optie 'FFT' op onze middenklasse oscilloscoop XDS2102A van OWON. De gele trace geeft het tijd domein weer, de paarse het frequentie domein van een periodieke smalle puls.
 |
De fourier-reeks van een smalle puls op het scherm van |
De fourier-reeks van een blokgolf
De coëfficiënten van de harmonischen
Men kan berekenen dat de fourier-reeks van een blokgolf uit de onderstaande termen bestaat:
- Eerste harmonische: [1,0 • sin(f)]
- Derde harmonische: [0,333 • sin(3f)]
- Vijfde harmonische: [0,2 • sin(5f)]
- Zevende harmonische: [0,143 • sin(7f)]
- Negende harmonische: [0,111 • sin(9f)]
- Elfde harmonische: [0,091 • sin(11f)]
Bij deze signaalvorm spelen dus alleen de oneven harmonischen een rol. Let u er bovendien even op dat de coëfficiënten van deze harmonischen precies gelijk zijn aan deze van de reeds behandelde zaagtand. Wonderbaarlijk!
Het tijd domein van een blokgolf
In de onderstaande figuur hebben wij weer sinussen met de juiste amplitude en de juiste frequentie een na een aan onze imaginaire menger aangeboden en iedere keer het resultaat op onze oscilloscoop bekeken.
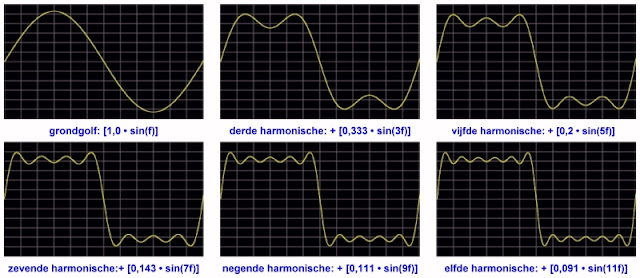 |
| De evolutie van een sinus naar een blok. (© 2021 Jos Verstraten) |
Het frequentie domein van een blokgolf
U kunt het grafiekje van het frequentie domein uit dat van de zaagtand afleiden door de even harmonischen te verwijderen.
 |
| Het weergeven van een rechthoek spanning in het frequentie domein. (© 2021 Jos Verstraten) |
De fourier-reeks van een periodieke smalle puls
Inleiding
In de onderstaande figuur ziet u een puls met een duty-cycle van 10 %. Dat betekent dat gedurende 10% van de periode de spanning hoog is en gedurende de overige 90% de spanning laag is. Zou zo'n periodieke puls ook met sinussen en cosinussen gemaakt kunnen worden? Laten wij het proberen!
 |
| Een periodieke puls met een duty-cycle van 10% is het laatste voorbeeld dat wij behandelen. (© 2021 Jos Verstraten) |
De coëfficiënten van de harmonischen
Men kan berekenen dat de fourier-reeks van een dergelijke smalle periodieke puls uit de onderstaande termen bestaat:
- Eerste harmonische: [1,0 • sin(f)]
- Tweede harmonische: [0,9 • cos(2f)]
- Derde harmonische: [0,8 • sin(3f)]
- Vierde harmonische: [0,7 • cos(4f)]
- Vijfde harmonische: [0,6 • sin(5f)]
- Zesde harmonische: [0,5 • cos(6f)]
- Zevende harmonische: [0,4 • sin(7f)]
- Achtste harmonische: [0,3 • cos(8f)]
- Negende harmonische: [0,2 • sin(9f)]
- Tiende harmonische: [0,1 • cos(10f)]
Het rekenkundig verband tussen de coëfficiënten is, als u er even over filosofeert, toch wel wonderlijk te noemen! Merk op dat bij deze fourier-reeks ook cosinus-signalen betrokken zijn.
Het tijd domein van een periodieke smalle puls
In de onderstaande figuur hebben wij weer sinussen en cosinussen met de juiste amplitude en de juiste frequentie een na een aan onze imaginaire menger aangeboden en iedere keer het resultaat op onze oscilloscoop bekeken.
 |
| De evolutie van een sinus naar een periodieke smalle puls. (© 2021 Jos Verstraten) |
Het frequentie domein van een periodieke smalle puls
In de onderstaande grafiek ziet u hoe een dergelijke smalle periodieke puls in het frequentie domein voorgesteld wordt.
 |
| Het weergeven van een smalle periodieke puls in het frequentie domein. (© 2021 Jos Verstraten) |
Koop uw UPS bij Amazon


