De geschiedenis van de Lissajous figuren
Wie was Lissajous?
De Franse natuur- en wiskundige Jules Antoine Lissajous, geboren in 1822 en gestorven in 1880, gaf zijn naam aan de Lissajous-figuren. Hij werd gefascineerd door trillingen en zijn voornaamste onderzoeksterrein was dus uiteraard akoestiek. Dat was immers, voor de ontdekking van elektriciteit en de elektromagnetische straling, hét natuurkundig gebied waarbij meetbare trillingen voorkwamen. Hij gebruikte lichtbundels en spiegels om het verband tussen de trillingen van diverse signalen zichtbaar te maken.
De 'harmonograaf'
Lissajous ontwikkelde de 'harmonograaf', waarmee de naar hem genoemde figuren gemaakt kunnen worden. Een harmonograaf maakt gebruik van twee slingers. Eén slinger beweegt een pen heen en weer ten opzichte van een as. De andere slinger beweegt het volledige tekenoppervlak ten opzichte van de loodrechte as. Door het variëren van de frequenties van de slingers worden verschillende patronen gecreëerd. Op die manier ontstaan ellipsen, spiralen of complexere Lissajous figuren op het tekenoppervlak. De vorm van de patronen geeft informatie over de fase- en frequentieverhoudingen tussen de twee slingers.
Eenvoudige harmonografen maken gebruik van één slinger en worden nu nog steeds aangeboden als kinderspeelgoed, zie de onderstaande figuur. De container aan de slinger heeft een kleine opening aan de onderzijde en is gevuld met zeer fijn gekleurd zand. Als de slinger in beweging wordt gezet zal deze allerlei bewegingen uitvoeren onder invloed van de zwaartekracht en ontstaat een fijn zandspoor op een vel papier.
 |
Een vereenvoudigde versie van een 'harmonograaf' als kinderspeelgoed. |
Lissajous figuren op een X-Y plotter
Met de ontwikkeling van de X-Y plotter in 1925 door Francis L. Moseley kreeg men een instrument in handen waarmee het heel gemakkelijk mogelijk werd Lissajous figuren op een vel papier te tekenen. Zo'n plotter bestaat uit een pen die door middel van twee motoren in twee loodrechte op elkaar staande richtingen over een vel papier kan worden gestuurd. De X-as wordt aangedreven door één sinusspanning, de Y-as door een tweede identieke spanning.
Professionele X-Y plotters, die worden gebruikt als uitvoer-apparaat van analoge computers, zijn erg duur. Gelukkig worden er tegenwoordig erg goedkope plottertjes aangeboden door Chinese firma's. Op de onderstaande foto ziet u zo'n apparaat dat voor ongeveer € 100,00 te koop is.
 |
| Een goedkope Chinese X-Y plotter. (© AliExpress) |
Met een dergelijk apparaat kunt u heel leuk experimenteren met het Lissajous principe en heel mooie kunstwerkjes produceren op een vel papier. U hebt er alleen twee goedkope heel laagfrequente sinusgeneratoren voor nodig. Ook die zijn voor een habbekrats in China als bouwpakketje te koop!
 |
Lissajous-achtige figuren uit een X-Y plotter. (© Stanford University) |
Lissajous figuren op een analoge oscilloscoop
Het zal duidelijk zijn dat een analoge oscilloscoop met een beeldbuis die vier afbuigelektroden bevat een ideaal instrument is voor het genereren van Lissajous figuren op een scherm. De tijdbasis worden dan uitgeschakeld en aan de afbuigelektroden die de horizontale afbuiging van de elektronenstraal veroorzaken wordt een sinusspanning aangesloten. Bij een tweekanaals oscilloscoop wordt hiervoor meestal CH2 gebruikt. Ook op het Y-kanaal (CH1) moet u een dergelijke spanning aanleggen.

De elektronenspot staat, als beide spanningen nul zijn, midden op het scherm. Een sinusspanning op het X-kanaal stuurt de spot van links naar rechts en vice versa. Een sinusspanning op het Y-kanaal stuurt de spot van onder naar boven en vice versa. Activeert u beide spanningen, dan ontstaan onderstaande afbeeldingen op het scherm van een analoge oscilloscoop.
 |
| Lissajous figuren op het scherm van een analoge oscilloscoop. (© Philip Broder) |
Lissajous figuren op een digitale oscilloscoop
Digitale oscilloscopen werken, per definitie, helemaal anders dan hun analoge soortgenoten. Zij hebben geen elektronenstraal en geen afbuigelektroden, dus de werking als Lissajous-demonstrator is niet zo voor de hand liggend als bij een analoog exemplaar. Het is uitsluitend de software die deze functie realiseert en vandaar dat de kwaliteit van het genereren van Lissajous figuren nogal verschilt van merk tot merk. In het onderstaand voorbeeld ziet u bijvoorbeeld de twee mogelijkheden die bij onze Owon XDS2102A kunnen worden geselecteerd.
De Lissajous-optie zit verborgen in het menu 'Display' en heet 'X-Y Mode'. Dit zal wel bij de meeste digitale apparaten het geval zijn.
 |
| Lissajous figuren op het scherm van een digitale oscilloscoop. (© 2022 Jos Verstraten) |
Hoe ontstaan Lissajous figuren?
Denk analoog!
Om het ontstaan van deze figuren te begrijpen moet u uw digitale oscilloscoop even vergeten en denken dat u weer een oud analoog instrument in handen hebt. Zo'n scoop heeft een kathodestraalbuis met aan de achterkant een elektronenkanon en aan de voorkant een fluorescerend scherm. Het kanon vuurt een dunne straal elektronen af op het scherm. Waar die elektronenbundel terecht komt zal het scherm oplichten. Tussen het kanon en het scherm staan vier elektroden, die de afbuigelektroden worden genoemd. Als tussen twee tegenover elkaar geplaatste elektroden een spanningsverschil wordt aangebracht zal dit een elektrisch veld genereren dat verantwoordelijk is voor een bepaalde afbuiging van de elektronenstraal. Twee elektroden zorgen voor de afbuiging in de horizontale richting (X), de twee andere voor de afbuiging in de verticale richting (Y)
 |
| Anatomie van een kathodestraalbuis. (© SPM Physics KSSM, edit 2022 Jos Verstraten) |
Identieke spanningen in fase aan beide kanalen
Stel nu dat u aan beide paren afbuigelektroden dezelfde sinusvormige spanning aanlegt. Dat wil zeggen dat zowel de frequentie, de amplitude als de fase van beide signalen identiek zijn. De spanning tussen de X-platen zorgt voor een afbuiging in de horizontale richting, de spanning tussen de Y-platen zorgt voor een identieke afbuiging in de verticale richting. Het gevolg is dat op het scherm van de kathodestraalbuis een mooie rechte lijn wordt geschreven onder een hoek van exact 45°.
Als u hieraan twijfelt kan de onderstaande figuur u misschien overtuigen. Zowel op het X- als op het Y-signaal is een aantal identieke tijdstippen geselecteerd en wordt de mate van afbuiging door de stippellijnen weergegeven. Daar waar de horizontale en verticale stippellijnen elkaar kruisen zal een lichtstip op het betreffende tijdstip op het scherm verschijnen.
De lichtstip gaat dus snel heen en weer over de getekende 45° lijn waardoor, dank zij de traagheid van het oog, de indruk van een rechte lijn ontstaat. Voor iedere periode van de signalen gaat de lichtstip twee keer heen en weer over de rechte lijn.
 |
| Lissajous figuur bij twee volledig identieke spanningen. (© 2022 Jos Verstraten) |
Hoe deze situatie er in de praktijk uitziet blijkt uit het onderstaande oscillogram. Hier hebben wij de uitgang van een sinusgenerator, ingesteld op 500 Hz, aangesloten op beide ingangskanalen van onze oscilloscoop. De gevoeligheden van beide kanalen werden identiek ingesteld.
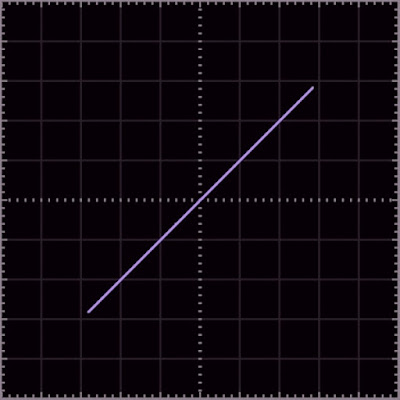 |
| Dit voorbeeld op het scherm van de oscilloscoop. (© 2022 Jos Verstraten) |
Het zal duidelijk zijn dat de hoek die de lijn maakt met de horizontale as alleen gelijk is aan 45° als beide spanningen exact even groot zijn. Als de spanning Uy bijvoorbeeld kleiner wordt, dan zal de lijn platter verlopen en is de genoemde hoek kleiner dan 45°.
Identieke spanningen in tegenfase aan beide kanalen
Stel vervolgens dat u de fase van een van de signalen 180° draait. Dat wil zeggen dat wél de frequentie en de amplitude identiek blijven, maar dat als het ene signaal zijn positieve halve periode doorloopt het andere signaal zijn negatieve halve periode doorloopt. Wat heeft dat tot gevolg voor de Lissajous figuur die op het scherm van uw oscilloscoop verschijnt?
Uit de onderstaande figuur volgt dat er weer een rechte lijn op het scherm verschijnt, maar nu onder een hoek van 135° ten opzichte van de horizontale as. Ook nu is het duidelijk dat die hoek kleiner of groter wordt als beide signalen een verschillende amplitude hebben.
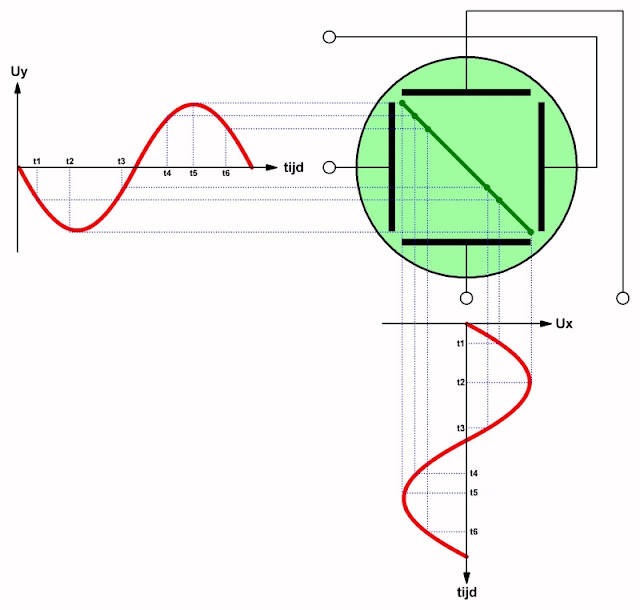 |
| Lissajous constructie bij twee signalen in tegenfase. (© 2022 Jos Verstraten) |
Een faseverschuiving van 90° tussen beide signalen
Een faseverschuiving van 90° wil zeggen dat het ene signaal maximaal positief of negatief is op het moment dat het andere signaal door de nul gaat. Wat wordt nu de Lissajous figuur? Dat blijkt uit de onderstaande figuur. Er verschijnt een mooie cirkel op het scherm.
Voorwaarde voor een cirkel is dat beide signalen even groot zijn. Is een van de signalen groter of kleiner dan het andere, dan wordt de cirkel een ellips. Wél staat de denkbeeldige lijn die de twee brandpunten f1 en f2 van de ellips verbindt ofwel perfect horizontaal ofwel perfect verticaal.
 |
| Een faseverschuiving van 90° tussen beide signalen. (© 2022 Jos Verstraten) |
Signalen met frequentie f en frequentie 2●f , in fase
Hiermee bedoelen wij dat de frequentie van het ene signaal het dubbele is van de frequentie van het andere signaal. Beide signalen zijn nog steeds even groot en in fase. De nulpunten van beide signalen vallen dus, voor zover van toepassing, precies samen.
U ziet dat er een soort van 90° gedraaid symbool van oneindigheid op het scherm wordt weergegeven. Dit plaatje staat alleen stil op het scherm als aan de formule:
fUx = 2 ● fUy
wordt voldaan. Zelfs bij de kleinste afwijking tussen beide frequentie gaat de afbeelding allerlei andere vormen aannemen, wij komen daar later nog op terug.
 |
| Het resultaat van f en 2 ● f. (© 2022 Jos Verstraten) |
Het nut van de Lissajous figuren
Meer dan een leuk stukje speelgoed
Tot nu toe lijkt het alsof deze oeroude techniek iets is om even leuk mee bezig te zijn en dan weer te vergeten. Dat doet de ontdekking van Lissajous onrecht aan! De figuren van Lissajous zijn zeer gevoelig voor de kleinste fase- of frequentie-ongelijkheid tussen twee signalen. Wij geven in de volgende paragrafen een paar voorbeelden.

Het zichtbaar maken van grote faseverschillen
Als u de fasehoek tussen twee signalen met identieke amplitude en frequentie laat stijgen van 0° tot 90° ziet u dat de rechte lijn onder een hoek van 45° bij nul graden faseverschuiving een ellips wordt die steeds meer op een cirkel gaat lijken. Bij 90° faseverschuiving ziet u een perfecte cirkel op het scherm. Deze transformatie van lijn naar cirkel is nog eens voor de duidelijkheid samengevat in de onderstaande figuur.
 |
| Fasehoeken van 0° tot 90°. (© 2022 Jos Verstraten) |
Het detecteren van zeer kleine faseverschillen
Deze transformatie van lijn naar cirkel is zeer gevoelig. In de onderstaande afbeelding ziet u bijvoorbeeld, van links naar rechts, de Lissajous figuren van twee identieke signalen met een onderling faseverschil van 0°, 2° en 4°. Zelfs deze kleine verschillen zijn dus goed te zien op het scherm van uw oscilloscoop.
Op deze manier kunt u bijvoorbeeld onderzoeken of beide kanalen van een stereoversterker hetzelfde fasegedrag hebben en zo nee, hoe groot de afwijkingen zijn in functie van de frequentie.
 |
| Het zichtbaar maken van zeer kleine faseverschillen. (© 2022 Jos Verstraten) |
Grote frequentieverschillen bestuderen
Frequentie die veelvouden van elkaar zijn laten zich gemakkelijk vangen in Lissajous figuren. In de onderstaande afbeelding ziet u bijvoorbeeld de figuren die ontstaan voor drie-, vier-, en vijfvoudige frequenties op de X-ingang ten opzichte van het signaal op de Y-ingang.
Let wel dat deze stilstaande figuren uitsluitend ontstaan als er geen faseverschuiving tussen de signalen aanwezig is. In de praktijk zal dat vrijwel nooit het geval zijn. Het patroon beweegt dus in de meeste gevallen dynamisch over het scherm, de animated gif in het begin van dit artikel is daar een mooi voorbeeld van.
 |
Veelvouden van de Y-frequentie op de X-ingang. (© 2022 Jos Verstraten) |
Kleine frequentieverschillen detecteren
Lissajous figuren zijn, onder voorwaarden, ook ideaal voor het detecteren van zeer kleine frequentieverschillen tussen sinusvormige signalen. Als voorbeeld ziet u de onderstaande oscillogrammen die ontstaan bij gelijke frequenties (links) en bij frequenties die 5 % of 10 % variëren. Dat komt bijvoorbeeld overeen met een signaal met een frequentie van 1,00 kHz aan de Y-ingang en een signaal met een frequentie van respectievelijk 1,05 kHz of 1,10 kHz aan de X-ingang.
 |
Het detecteren van kleine frequentieverschillen. (© 2022 Jos Verstraten) |
Berekenen van de faseverschuiving
Alleen bruikbaar als frequentie en amplitude identiek zijn
Als u de fase van twee even grote signalen met bovendien dezelfde frequentie vergelijkt kunt u uit de gegevens op het scherm van uw oscilloscoop de waarde van het faseverschil berekenen.
De werkwijze is voorgesteld in de onderstaande figuur:
- U zet de ellips die op het scherm verschijnt met de positie-regelaars van beide ingangskanalen precies in het midden van het scherm.
- U meet de halve maximale hoogte A van de ellips.
- U meet de hoogte B tussen de X-as en het punt waar de ellips de Y-as snijdt.
- Deel vervolgens B door A.
- Dit getal met een waarde kleiner dan 1 is de sinus van de fasehoek tussen beide signalen.
- Dat getal kunt u in een 'sinustabel' (zoek op Google) opzoeken en u leest de daarbij horende hoek af uit de tabel.
- Deze hoek is de fasehoek tussen beide signalen
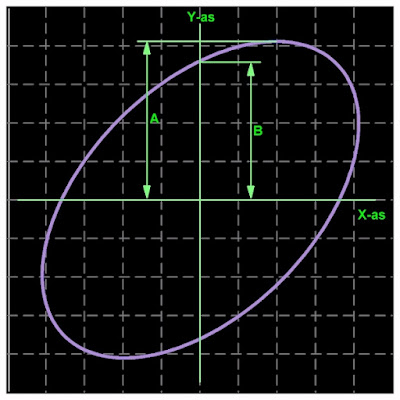 |
| Het berekenen van faseverschillen. (© 2022 Jos Verstraten) |
Een voorbeeld
In het getekende voorbeeld meten wij op de printout van ons oscilloscoopscherm:
A = 102,5 mm
en
B = 89,8 mm
Delen van B door A levert:
Sinus van de fasehoek = 89,8 / 102,5
Sinus van de fasehoek = 0,876
Uit een sinustabel kunt u aflezen dat een sinuswaarde van 0,876 overeen komt met een hoek van ongeveer 61°.
Hiland M12864 LCR ESR PWM Transistor Tester Kit


