
|
De natuurkunde houdt zich bezig met het onderzoeken van verschijnselen in de natuur die gekenmerkt worden door grootheden: afmetingen, massa, temperatuur en misschien snelheid.
|
Grootheden en hun eigenschappen
Definitie van grootheid
Zuiver natuurkundige bekeken is een grootheid een eigenschap die kwantificeerbaar is, zoals massa, temperatuur of afstand. Als u op uw thermometer in uw tuin ziet dat het 15 °C is, dan begrijpt iedereen wat u gemeten hebt. De grootheid 'temperatuur' wordt hierbij cijfermatig uitgedrukt in een eenheid '°C' of 'graden celsius'. Hiermee is de temperatuur in uw tuin ondubbelzinnig vastgesteld, er kunnen geen meningsverschillen over ontstaan. Maar daarvoor is het nodig dat er overeenstemming bestaat over de gebruikte eenheid.
| FORMULES IN DIT ARTIKEL |
|---|
| VERMENIGVULDIGEN:
Het vermenigvuldigingsteken wordt voorgesteld door een bullet tussen de factoren: a • b = c DELEN: Het gedeeld door teken wordt voorgesteld door een schuine streep: a / b = c |
De eenheid van grootheden
In de praktijk van de natuurkunde is het ondubbelzinnig meten en definiëren van grootheden van fundamenteel belang. Een Amerikaanse natuurkundige die het kookpunt van een vloeistof bepaalt, moet dezelfde temperatuur meten als zijn Europese beroepsgenoot. Onder het meten van een grootheid verstaat men deze grootheid vergelijken met een soortgelijke grootheid, die men tot eenheid heeft gekozen. Zo heeft men eeuwen lang voor de eenheid van afstand de lengte genomen van een bepaalde staaf metaal die in Frankrijk werd bewaard. Deze eenheid werd 'de meter' genoemd. Op deze manier was iedereen in staat zijn of haar eigen eenheid van lengte te ijken op deze internationale standaard, de meter.
Grootheden te kust en te keur
Er bestaan uiteraard ontelbare grootheden. Alleen in de elektrotechniek kunt u zonder diep na te denken meer dan tien grootheden opnoemen:
- Capaciteit met als eenheid de farad (F).
- Elektrische geleidbaarheid met als eenheid de siemens (S).
- Frequentie met als eenheid de hertz (Hz).
- Golflengte met als eenheid de meter (m).
- Lading met als eenheid de coulomb (Q).
- Magnetische flux met als eenheid de weber (Wb).
- Magnetische Reluctantie met als eenheid de ampère-winding per weber (aw/Wb).
- Spanning met als eenheid de volt (V).
- Stroom met als eenheid de ampère (A).
- Veldsterkte met als eenheid volt per meter (V/m).
- Vermogen met als eenheid de watt (W).
- Weerstand met als eenheid de ohm (Ω).
- Zelfinductie met als eenheid de henry (H).
Zeven fundamentele grootheden
Al deze grootheden hebben uiteraard een eigen eenheid, maar het is in de praktijk een vrijwel onmogelijke klus om voor al deze eenheden internationale standaarden af te spreken. Dank zij de wiskunde hoeft dat niet. Men heeft kunnen aantonen dat er slechts zeven fundamentele grootheden bestaan, waaruit alle overige grootheden wiskundig afgeleid kunnen worden.
- Lengte met als eenheid de meter (m).
- Massa met als eenheid de kilogram (kg).
- Tijd met als eenheid de seconde (s).
- Elektrische stroom met als eenheid de ampère (A).
- Temperatuur met als eenheid de graad kelvin (°K).
- Hoeveelheid materie met als eenheid de mol (mol).
- Lichtsterkte met als eenheid de candela (cd).
De symbolen van grootheden
Naast eenheden hebben grootheden ook nog symbolen. Dat zijn de afkortingen, waarmee zij in wiskundige formules worden voorgesteld. De vijf fundamentele grootheden hebben de onderstaande symbolen.
- Lengte: s.
- Massa: m.
- Tijd: t.
- Elektrische stroom: I.
- Temperatuur: T.
- Hoeveelheid materie: N.
- Lichtsterkte: Iv.
Het groothedenstelsel dat van deze zeven basisgrootheden is afgeleid noemt men het 'internationale MKS-stelsel' naar de eerste letters van de drie oudste fundamentele eenheden meter, kilogram en seconde. In de techniek wordt hiervoor nog vaak het verouderde woord 'Giorgistelsel' gebruikt.
De eenheden van de basisgrootheden
De seconde
De seconde is de duur van 9.192.631.770 trillingen van de straling die wordt uitgezonden tussen twee bepaalde energieniveaus van een atoom Cesium133.
De meter
De meter is gelijk aan de afstand die het licht in het luchtledige aflegt in 1/299.792.458-ste deel van een seconde.
De kilogram
De kilogram is de massa van een bepaalde cilinder, gemaakt van platina-irridium, die wordt bewaard te Sèvres in Frankrijk. De kilogram is de enige ijkwaarde die is afgeleid van een door de mens gemaakt voorwerp in plaats van een natuurkundige eigenschap. Het is ook de enige ijkwaarde die een voorvoegsel (kilo) in de naam heeft staan.
 |
| De standaard kilogram. (Greg L Wikimedia Commons) |
De ampère
De ampère is de stroom die door twee op een afstand van 1 m parallel gespannen draden vloeit en die tussen de draden een aantrekkingskracht van 2 • 10-7 newton per meter lengte veroorzaakt. Als er in uw huis een elektrische stroom van 1 A wordt afgenomen van het net, dan betekent dit dat u ongeveer 230 W vermogen verbruikt, oftewel zes gloeilampen van 40 W laat branden.
De graad kelvin
De graad kelvin is het 1/273,16-de deel van de tripeltemperatuur van zuiver water. Het tripelpunt is de toestand waarbij water tegelijkertijd voorkomt in zijn drie aggregatietoestanden: vast (ijs), vloeibaar (water) en gasvormig (waterdamp). Alweer zo'n weinig tot de verbeelding sprekende definitie, maar 0 °K komt overeen met -273,15 °C. Dat is de allerlaagste temperatuur die in het heelal kan voorkomen.
De mol
Een mol is de hoeveelheid materie van een bepaalde stof die evenveel deeltjes bevat als er atomen zijn in 12 gram koolstof12. Het aantal deeltjes in zo'n ene mol is gelijk aan niet minder dan 6,022.14 • 1023.
De candela
De candela geeft aan hoeveel licht zich bevindt in een oppervlak van een lichtbundel. Eén candela is gelijk aan de lichtsterkte in een bepaalde richting uitgestraald door een bron die licht van één kleur uitzendt met een frequentie van 540 • 1012 Hz en waarvan de stralingssterkte in die richting 1/683 W per standaard ruimtehoek is. Zegt u dat niets? Misschien dit dan wél: één candela komt ongeveer overeen met de lichtstrekte van een kaars.
Kan het niet wat gemakkelijker?
Het valt op dat zes van de zeven eenheden van de basisgrootheden niet op de allergemakkelijkste manier zijn gedefinieerd. Dat heeft historische achtergronden. Deze fundamentele grootheden zijn al eeuwenlang bekend. De eenheden werden in die tijd vrij willekeurig toegekend, zo goed als dat kon met de toen ter beschikking staande meettechnieken. Bij het herdefiniëren van deze eenheden in het internationale eenhedenstelsel was het natuurlijk zaak definities te vinden die in een modern laboratorium goed reproduceerbaar zijn maar die bovendien precies dezelfde waarden opleverden als de oude definities. Het zou natuurlijk beter zijn geweest om zeven geheel nieuwe definities op te stellen die veel eenvoudiger zijn. Maar dat zou tot gevolg hebben dat men overal in de wereld alle natuurkundige grootheden opnieuw zou moeten omrekenen met de nieuwe eenheden als basis. Dat zou een echte revolutie hebben ontketend, een onmogelijke opgave.
Afgeleide grootheden
De volt als voorbeeld
Alle andere grootheden noemt men afgeleide grootheden, omdat zij uit een combinatie van de fundamentele grootheden kunnen worden afgeleid. Zo zou u kunnen berekenen dat de praktische eenheid van elektrische spanning, de aan iedere elektronicus zeer bekende volt (V), ook uitgedrukt kan worden als:
1 V = 1 kgm2/As3

Een gemakkelijker voorbeeld is snelheid
Een ander, gemakkelijker, voorbeeld is snelheid. In het MKS-stelsel wordt snelheid uitgedrukt in de eenheid 'm/s', oftewel 'meter per seconde'. Omdat dit in het dagelijks leven een onpraktische eenheid is, werkt men meestal met de eenheid 'km/h', oftewel 'kilometer per uur'. Maar deze eenheid is uiteraard afgeleid van de MKS-eenheid:
1 km/h = 1.000 m/h = 1.000/3.600 m/s = 0,277.777 m/s
Als u met uw auto met een snelheid van 100 km/h rijdt, dan legt u 27,777 meter per seconde af. Bij 130 km/h is dat al 36,11 meter per seconde. Toch een gegeven om even stil bij te blijven staan.
Voorvoegsels of prefixen
Te groot of te klein
De meeste eenheden zijn voor de dagelijkse praktijk veel te groot of veel te klein gedefinieerd. Zo zal wel geen enkele elektronicus een condensator van 1 F in huis hebben. Nu zou u dus de waarde van een klein condensatortje in een afstemkring van uw tv kunnen schrijven als 0,000.000.000.047 F. Dat is vrij onhandig en vandaar zijn er negentien zogenoemde voorvoegsels of prefixen ingevoerd waarmee u de waarde van een eenheid kunt vermenigvuldigen.
De negentien standaard voorvoegsels
| Vermenigvuldigingsfactor | Naam | Symbool | In gewone taal geschreven |
|---|---|---|---|
| 1.000.000.000.000.000.000.000 = 1021 | zetta | Z | triljard |
| 1.000.000.000.000.000.000 = 1018 | exa | E | triljoen |
| 1.000.000.000.000.000 = 1015 | peta | P | biljard |
| 1.000.000.000.000 = 1012 | tera | T | biljoen |
| 1.000.000.000 = 109 | giga | G | miljard |
| 1.000.000 = 106 | mega | m | miljoen |
| 1.000 = 103 | kilo | k | duizend |
| 100 = 102 | hecto | h | honderd |
| 10 = 101 | deca | da | tien |
| 0,1 = 10-1 | deci | d | een tiende |
| 0,01 = 10-2 | centi | c | een honderdste |
| 0,001 = 10-3 | milli | m | een duizendste |
| 0,000.001 = 10-6 | micro | µ | een miljoenste |
| 0,000.000.001 = 10-9 | nano | n | een miljardste |
| 0,000.000.000.001 = 10-12 | pico | p | een biljoenste |
| 0,000.000.000.000.001 = 10-15 | femto | f | een biljardste |
| 0,000.000.000.000.000.001 = 10-18 | atto | a | een triljoenste |
| 0,000.000.000.000.000.000.001 = 10-21 | zepto | z | een triljardste |
| 0,000.000.000.000.000.000.000.001 = 10-24 | yokto | y | een quadriljoenste |
Voorbeelden
1 cm = 0,01 m = een honderdste meter
1 µF = 0,000.001 F = een miljoenste farad
1 MΩ = 1.000.000 Ω = een miljoen ohm
1 fm = 0,000.000.000.000.001 m = een biljardste meter
Scalaire contra vectoriële grootheden
Scalaire grootheden
De meeste grootheden zoals massa, temperatuur en tijd kunnen volledig gedefinieerd worden door hun waarde en hun eenheid. Als u beweert dat een bepaald lichaam een massa van 1,24 kg heeft, dan is de massa van dat lichaam daardoor volledig vastgelegd, geen discussie mogelijk. Dergelijke grootheden noemt men 'scalaire' grootheden.
Vectoriële grootheden
Bij sommige grootheden zoals bijvoorbeeld snelheid, ligt dat anders. Snelheden hebben namelijk niet alleen een waarde in m/s, maar ook een richting waarin zij werken. Bovendien hebben zij een aangrijpingspunt en een zin. Een grootheid die wordt gedefinieerd door een waarde, een richting, een zin en een aangrijpingspunt noemt men een 'vectoriële' grootheid.
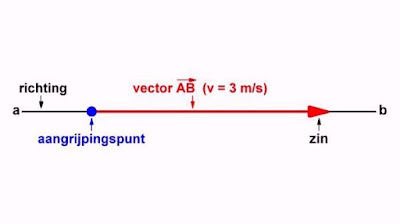 |
| Voorstelling van een vectoriële grootheid. (© - 2017 Jos Verstraten) |
Rekenen met grootheden
Rekenen met scalaire grootheden
Scalaire grootheden kunnen bij elkaar opgeteld of van elkaar afgetrokken worden. Als u een helikopter ziet op een hoogte van 100 meter en uit deze helikopter hangt een hijskabel van 40 meter lengte, dan is het duidelijk dat de haak van die kabel op een hoogte van 60 meter hangt. Bij vectoriële grootheden ligt dat iets ingewikkelder.
Vectoren met dezelfde richting optellen
Een van de belangrijkste bewerkingen die u op vectoren moet uitvoeren is twee vectoren bij elkaar optellen. Dat gaat niet zo gemakkelijk als bij scalaire grootheden! De som van twee vectoren is een nieuwe vector, die de resultante wordt genoemd. Als de twee vectoren hetzelfde aangrijpingspunt en dezelfde richting hebben, dan is er geen probleem. In het bovenste voorbeeld werken twee snelheidsvectoren A en B in op hetzelfde aangrijpingspunt. Beide vectoren hebben dezelfde richting en dezelfde zin. De ene vector is 1 m/s groot, de andere 2 m/s. De resultante heeft een waarde van 3 m/s en uiteraard dezelfde richting en zin. In het onderste voorbeeld is getekend wat er gebeurt als beide vectoren een tegengestelde zin hebben. De vector A werkt men 1 m/s naar links, de vector B met 2 m/s naar rechts. De resultante is een vector met een waarde van 1 m/s, die naar rechts werkt.
 |
| Optellen van vectoren die in elkaars verlengde liggen. (© - 2017 Jos Verstraten) |
Vectoren met verschillende richtingen optellen
Het wordt echter iets moeilijker als de twee vectoren in verschillende richtingen aangrijpen. In het aangrijpingspunt O werken twee snelheidsvectoren in. De eerste A heeft een horizontale richting en een grootte van 4 m/s. De tweede B staat onder een hoek van 60° naar boven en heeft een grootte van 2 m/s. De resultante kan meetkundig geconstrueerd worden door met de vectoren A en B als zijden een parallellogram te tekenen. De resultante C is dan gelijk aan de diagonaal die vertrekt uit het aangrijpingspunt. Met simpele wiskundige middelen kunt u berekenen dat de waarde van de resultante gelijk is aan 5,6 m/s.
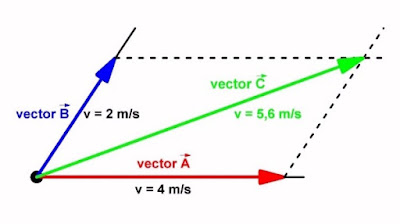 |
| Optellen van vectoren die een hoek met elkaar maken. (© - 2017 Jos Verstraten) |
Een praktisch voorbeeld
U kunt dit voorbeeld vertalen naar een praktische situatie. Stel dat u een weiland bezit waar op een plek een zwaar rotsblok ligt. U wilt dit rotsblok verwijderen en spant door middel van twee stevige touwen twee tractoren in, die beide aan het blok gaan trekken. De ene tractor A vertrekt in horizontale richting met een snelheid van 4 m/s. De tweede tractor B trekt onder een hoek van 60° met een snelheid van 2 m/s. Dank zij de vectorwiskunde kunt u nu berekenen in welke richting en met wat voor snelheid het rotsblok wordt verplaatst. De snelheid van het blok bedraagt 5,6 m/s, de richting is naar C.

Ontbinden van vectoren
Een tweede belangrijke bewerking die u op vectoriële grootheden kunt uitvoeren is het ontbinden in twee deelvectoren langs de horizontale en verticale richtingen. In de illustratie is een vector C getekend, die in een bepaalde richting aangrijpt in punt O. Deze vector kan ontbonden worden in twee deelvectoren A en B, die verlopen volgens de loodrechte richtingen a en b. Het volstaat een rechthoek te tekenen, waarbij de vector C de diagonaal vormt en de twee componentvectoren A en B de twee aansluitende zijden. Door het ontbinden van vectoren in een horizontale en verticale component kunt u ingewikkelde vectorberekeningen ten zeerste vereenvoudigen.
 |
| Ontbinden van een vectoriële grootheid volgens twee richtingen. (© - 2017 Jos Verstraten) |

|

|
Koop uw soldeerbout bij Banggood
