
|
Brugschakelingen zijn gebalanceerde netwerken waarin vier componenten het verband tussen de ingangs- en de uitgangsspanning vastleggen. 
|
Kennismaking met het begrip brugschakeling
Het fundamentele schema van een brug
In de onderstaande figuur is het algemeen schema van een brugschakeling weergegeven. De schakeling wordt meestal ruitvormig getekend (linker schema), maar kan ook traditioneel met uitsluitend horizontale en verticale verbindingslijnen worden getekend (rechter schema).
De vier blokjes Z1, Z2, Z3 en Z4 kunnen allerlei elektronische onderdelen voorstellen zoals weerstanden, condensatoren, spoelen, diodes, transistoren of schakelaars.
 |
| Het algemeen schema van een brug. (© 2022 Jos Verstraten) |
Zwevende in- en uitgangen
Bij de meeste elektronische schakelingen heeft de ingang een 'hete' ader en een 'massa' ader. Hetzelfde geldt voor de uitgang. Zowel de in- als de uitgang hebben dus één ader gemeenschappelijk. Dat maakt het verwerken van signalen in zo'n schakeling gemakkelijk. Ook het meten in zo'n schakeling is dan eenvoudig omdat ook de meeste meetinstrumenten een 'hete' ader en een 'massa' ader hebben.
Dat is bij een brugschakeling anders. Een van de fundamentele eigenschappen van een brugschakeling is namelijk dat zowel de ingang als de uitgang zweven ten opzichte van de massa van de schakeling. U ziet in het schema immers heel duidelijk dat er geen gemeenschappelijke ader is bij de in- en uitgang. Bij het meten in brugschakelingen met uw geaarde instrumenten moet u dus heel goed letten op deze fundamentele eigenschap van een brugschakeling. Sluit u bijvoorbeeld uw sinusgenerator aan op de ingang van een brug en uw oscilloscoop op de uitgang, dan sluit u per definitie een van de vier blokjes Z1, Z2, Z3 of Z4 kort!
Een brug in evenwicht
Een aantal brugschakelingen wordt gebruikt voor het nauwkeurig meten van de waarde van een weerstand, condensator of spoel. Bij dergelijke bruggen wordt het te meten onderdeel bijvoorbeeld in het blokje Z3 geplaatst en wordt het blokje Z1 ingevuld door bijvoorbeeld een zeer nauwkeurig in te stellen weerstand. De uitgangsklemmen worden aangesloten op een heel gevoelige meter. De ingangsklemmen worden verbonden met een spanningsbron. Afhankelijk van de toepassing kan dat gelijk- of wisselspanning zijn. De instelbare weerstand Z1 wordt dan zo verdraaid tot er tussen de twee klemmen van de uitgang geen spanning of signaal aanwezig is. Men zegt dan dat de brug 'in evenwicht' of 'in balans' is. Uit de waarde van de weerstand in Z1 kunt u dan met een meestal eenvoudige formule de waarde van het te meten onderdeel in Z3 berekenen.
De weerstanden decadenbank
Voor dergelijke 'brug in evenwicht'-metingen hebt u altijd een weerstanden decadenbank nodig. Met zo'n decadenbank kunt u een weerstand zeer nauwkeurig instellen, soms zelfs tot op ±0,1 % nauwkeurig.
In de onderstaande figuur zijn twee uitvoeringen van zo'n instrument voorgesteld. Bij de linker moet u de gewenste weerstand samenstellen door met de schuifschakelaars combinaties van 1-2-3-4, 10-20-30-40, etc. waarden in of uit te schakelen. De rechter bestaat uit een aantal tienstanden draaischakelaars waarmee u de gewenste weerstand snel kunt selecteren.
 |
| Twee weerstanden decaden banken. (© 2022 Jos Verstraten) |
Dergelijke decadenbanken zijn vrij prijzig. Een goedkoop alternatief is in de onderstaande foto voorgesteld. Met zo'n 'weerstanden decaden print' kunt u hetzelfde, maar met iets meer moeite en minder nauwkeurig. Zo'n printje bestaat, per decade, uit negen even grote in serie geschakelde weerstanden van bijvoorbeeld 1 kΩ en even veel tweepolige print-headers. Met een jumper kunt u een van deze headers kortsluiten waardoor u bijvoorbeeld vijf van de negen weerstanden inschakelt en een totale weerstand van 5 kΩ selecteert.
 |
| Een goedkoop alternatief voor een weerstanden decaden bank. (© AliExpress) |
Een dergelijk printje is op dit blog getest in een eigen artikeltje:
Aanklikbare link ➡ Hobby-lab: weerstand decaden print
Opmerking
Dergelijke decadenbanken zijn ook op de markt met condensatoren in plaats van met weerstanden.
De galvanometer voor gelijkspanningsbruggen
Een tweede onmisbaar attribuut bij het uitvoeren van 'brug in evenwicht'-metingen is een zeer gevoelige meter die zowel positieve als negatieve spanningen of stromen kan meten. Daar kunt u uiteraard uw digitale multimeter voor gebruiken. Maar omdat u de brug moet afregelen op minimale waarde van de stroom in de uitgang en die stroom zowel positief als negatief kan zijn is het handig als u daarvoor een naaldmeter gebruikt met het nulpunt in het midden van de schaal. Dan ziet u heel mooi hoe bij het afregelen van de brug de naald van de meter langzaam maar zeker het midden van de schaal opzoekt. Zo'n meter wordt 'galvanometer' genoemd en is voor een tot twee tientjes te koop bij de bekende Chinese verkoopplatformen. Koop er wel eentje die intern door twee diodes is beschermd tegen overbelasting!
 |
Een galvanometer is handig als u 'brug in evenwicht'-metingen |
Een alternatief voor wisselspanningsbruggen
Een brug in evenwicht brengen met een galvanometer is uitsluitend mogelijk als deze brug wordt gevoed met een gelijkspanning. Er bestaan echter ook bruggen die u met een wisselspanning moet voeden, bijvoorbeeld voor het meten van een spoel of een condensator. U kunt dan geen galvanometer toepassen en moet een gevoelige wisselstroom- of wisselspanningsmeter in de diagonaal zetten. Een goedkope oplossing is gebruik te maken van een gevoelige hoofdtelefoon. U voedt de brug dan met een wisselspanning van bijvoorbeeld 1 kHz en regelt de brug af op minimaal geluid uit de hoofdtelefoon. Zorg ervoor, door de meting te beginnen met een kleine spanning, dat u uw oren niet overbelast!
Soorten van brugschakelingen
Bij ons uitgebreid literatuur onderzoek, de bron van dit artikel, hebben wij niet minder dan vijftien brugschakelingen ontmoet. Sommige daarvan kent u al onder een andere naam en gebruikt u vaak zonder te vermoeden dat deze tot de familie der brugschakelingen behoren. Andere zijn verouderd, zeer zeldzaam en of extreem en zult u in uw dagelijkse elektronica praktijk zelden tot nooit tegenkomen.
In de volgende hoofdstukken behandelen wij:
- Graetz-brug
- H-brug
- Versterker-brug
- Wheatstone-brug
- Kelvin-brug, ook Thomson-brug genoemd
- Maxwell-brug
- Wien-brug
- De Sauty-brug
- Schering-brug
- Murray-brug
- Carey-Foster-brug
- Anderson-brug
- Hay-brug
- Fontana-brug
- Lattice-brug
Graetz-brug
Functie van de Graetz-brug
Deze brugschakeling kent u maar al te goed onder de naam 'bruggelijkrichter'. Het is de overbekende schakeling die u gebruikt om de secundaire wisselspanning van een voedingstrafo gelijk te richten.
Uitvinding van de Graetz-brug
Deze schakeling werd voor het eerst toegepast in december 1895 door de Poolse elektrotechnicus Karol Pollak. Twee jaar later werd zij, naar eigen zeggen zonder kennis van de Poolse schakeling, ook door de Duitse fysicus Leo Graetz uitgevonden en gepatenteerd. Vandaar dat deze schakeling onder zijn naam door het leven gaat.
De samenstelling van de Graetz-brug
In de onderstaande figuur is de samenstelling en functie van de Graetz-brug in een gelijkricht schakeling voorgesteld. De schakeling bestaat uit vier identieke dioden D1 tot en met D4. Deze staat per twee parallel geschakeld tussen de twee aansluitingen van de secundaire van de trafo. De twee parallelle ketens bestaan uit twee in anti-serie geschakelde dioden. De twee diodes D1 en D3 die met de kathodes aan elkaar hangen leveren de positieve pool van de gelijkgerichte spanning. De twee diodes D2 en D4 die met de anodes aan elkaar hangen leveren de negatieve pool van de gelijkspanning.
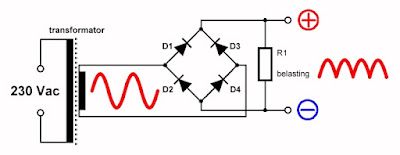 |
| De bekende brug van Graetz. (© 2022 Jos Verstraten) |
Het stroomverloop
In de onderstaande figuur is getekend hoe de stroom door de Graetz-brug loopt bij de positieve (rood) en bij de negatieve (blauw) halve sinus van de trafospanning. Bij de positieve halve sinus gaan de diodes D1 en D4 geleiden, bij de negatieve halve sinus de diodes D3 en D2. In beide gevallen loopt de stroom dus in dezelfde richting door de belastingsweerstand. Vandaar dat men zegt dat op de uitgang van de brug een GELIJKspanning staat, hoewel deze niet constant is, maar honderd keer per seconde een cyclus van nul naar maximum naar nul doormaakt.
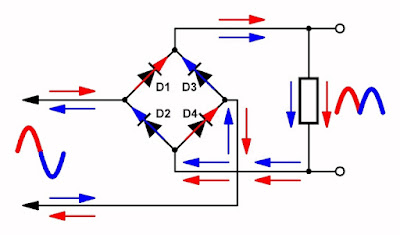 |
| Het stroomverloop door de schakeling. (© 2022 Jos Verstraten) |
Afvlakking
De brug van Graetz levert weliswaar een gelijkspanning aan de uitgang, maar deze spanning is niet bruikbaar als voedingsspanning. Vandaar dat de brug wordt afgesloten met een grote elektrolytische condensator C1. Deze dient als ladingsreservoir en houdt de uitgangsspanning min of meer constant op de topwaarde van de sinusspanning minus de spanningsval over de twee geleidende dioden. Uit de oscillogrammen in de onderstaande figuur volgt dat de diodes nu niet altijd stroom voeren. Deze onderdelen gaan maar eerst geleiden op het moment dat de van de trafo aangevoerde spanning groter wordt dan de spanning over de condensator. Alleen dan, voorgesteld door de rose perioden, gaat er een stroom door de halfgeleiders vloeien die er voor zorgt dat de condensator C1 weer wordt opgeladen. De spanning over dit onderdeel stijgt.
 |
Het afvlakken van de gelijkgerichte trafospanning. (© 2022 Jos Verstraten) |
De Graetz-brug in de praktijk
U kunt de gelijkrichter samenstellen uit vier losse diodes, zoals van het type 1N4007. Er bestaan echter diverse kant-en-klare Graetz-bruggen. De onderstaande foto geeft een impressie van de beschikbare uitvoeringen.
 |
Een paar voorbeelden van Graetz-bruggen. |
H-brug
Functie van de H-brug
Deze schakeling kunt u gebruiken voor het ompolen van de richting van de stroom die door een motor vloeit. Vandaar dat deze schakeling heel vaak wordt toegepast in schakelingen in de robotica. Deze brug dankt zijn naam niet aan een persoon, maar aan de typische H-vorm waarmee zij (tegenwoordig ook hij) in schema´s verschijnt.
De samenstelling en werking van de H-brug
In de onderstaande figuur wordt de fundamentele samenstelling van de H-brug voorgesteld. De vier schakelaars S1, S2, S3 en S4 kunnen alles zijn dat schakelt: relais, bipolaire transistoren, FET's en MOSFET's. Vanwege hun uitstekende schakeleigenschappen worden tegenwoordig hoofdzakelijk MOSFET's toegepast. Deze onderdelen worden gestuurd met vier signalen U1 tot en met U4 die binair zijn. Zij zijn of 'L', of 'H'. Bij 'H' wordt de betreffende schakelaar gesloten.
De onderstaande combinaties zijn mogelijk:
- U1 en U4 'H': de motor draait rechtsom
- U2 en U3 'H': de motor draait linksom
- U1 en U3 'H': de motor wordt kortgesloten en remt.
- U2 en U4 'H': de motor wordt kortgesloten en remt.
- Geen of slechts een signaal 'H': de motor staat in de vrijloop.
 |
De principiële schakeling van de H-brug. (© 2022 Jos Verstraten) |
- U1 en U2 'H'
- U3 en U4 'H'
nooit mogen voorkomen. Deze combinaties veroorzaken namelijk een kortsluiting tussen de plus en de min van de voedingsspanning. Vandaar dat de zekering F1 in het schema aanwezig is. Uiteraard wordt een H-brug in de praktijk niet gestuurd uit vier signalen, maar uit slechts twee. De decodering van twee naar vier signalen zit tegenwoordig in een IC. Met wat interne logica is te voorkomen dat de genoemde kortsluit-situaties in de praktijk kunnen ontstaan.
Een H-brug met bipolaire transistoren
In de onderstaande figuur is een schema getekend waarin een motor M wordt gestuurd uit vier 'werkpaarden van de elektronica', de 2N3055. Als U1 'H' is wordt transistor T1 in verzadiging gestuurd via de weerstand R1 en T4 via de weerstand R4. Er loopt stroom van links naar rechts door de motor. Als U2 'H' wordt gebeurt hetzelfde met de transistoren T2 en T3. De stroom loopt dan van rechts naar links door de motor. Bij deze schakeling mag de situatie U1 = U2 = 'H' niet voorkomen, want dan geleiden de vier transistoren en ontstaan er twee kortsluitingen tussen +Ub en GND.
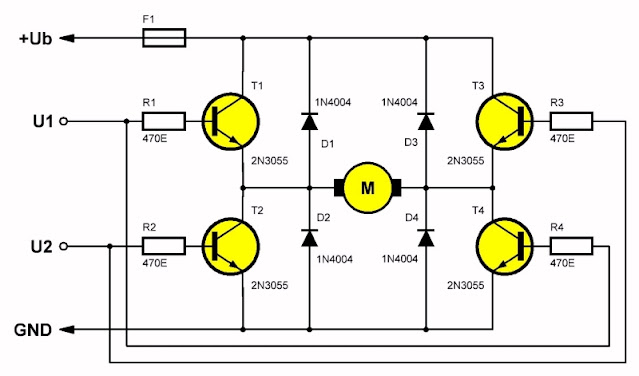 |
| Een H-brug met 4 x 2N3055. (© 2022 Jos Verstraten) |
Een H-brug met moderne N-MOSFET's
Het zal duidelijk zijn dat N-MOSFET's ideale onderdelen zijn voor het samenstellen van zo'n brug. De uiterst lage AAN-weerstand van dergelijke transistoren zorgt voor weinig vermogensverlies en voor weinig extra koeloppervlak. Als u echter zo'n brug wilt uitvoeren met vier stuks N-MOSFET's zit u met het probleem dat twee van die transistoren een high side belasting moeten sturen en twee een low side belasting. De high side halfgeleiders moeten op de gate een stuurspanning ontvangen die hoger is dan de voedingsspanning. Gelukkig zijn ook hiervoor complete driver-IC's ontwikkeld, zoals de HIP4081A van Renesas die u voor ongeveer € 5,00 kunt aanschaffen en bruikbaar is voor voedingsspanningen tot +15 V. Het door de fabrikant voorgeschreven schema is getekend in de onderstaande figuur.
De schakeling heeft een ingebouwd netwerk dat ervoor zorgt dat de high side en de low side MOSFET's met een kleine vertraging ten opzichte van elkaar uit- en inschakelen. Op deze manier worden zeer grote spike-stromen voorkomen.
 |
| Een H-brug met een HIP4081A driver en 4 x N-MOSFET. (© 2022 Jos Verstraten) |
Versterker-brug
Functie van de versterker-brug
Met een dergelijke schakeling kunt u, althans in theorie, het maximale vermogen dat in een bepaalde luidspreker met een bepaalde voedingsspanning wordt opgewekt verviervoudigen.
Het basisschema van de versterker-brug
In de onderstaande figuur is de koppeling tussen de luidspreker en eindversterker-brug voorgesteld. Bij deze brugschakeling zit de luidspreker tussen twee identieke eindtrappen. Het grote voordeel van deze configuratie is dat er een maximaal vermogen uit de beschikbare voedingsspanning naar de luidspreker wordt gestuurd. Vandaar dat u deze brugschakeling voornamelijk aantreft bij eindversterkers die met een lage spanning worden gevoed, zoals versterkers voor auto's die het met 12 V voeding moeten stellen of versterkers die vanuit een 5 V USB-poort worden gevoed. Nadeel is dat u de twee eindtrappen met signalen moet sturen die in tegenfase zijn. Als het signaal U1 aan de ene ingang positief stijgt, dan moet het signaal U2 aan de tweede ingang evenveel negatief dalen. U moet dus een extra trap tussenvoegen, die het ingangssignaal 180 graden in fase draait.
 |
| Het principeschema van een versterker-brug. (© 2022 Jos Verstraten) |
Luidspreker niet aan de massa!
Een tweede nadeel is dat de luidspreker niet aan de massa hangt. Beide aansluitingen van dit onderdeel voeren een signaalspanning ten opzichte van de massa. In de dagelijkse praktijk hebt u daar geen last van. Dit is wél een probleem als u wilt meten in een brugschakeling. Bij een normale versterker met de luidspreker aan de massa kunt u een sinusgenerator op de ingang en een oscilloscoop op de uitgang aansluiten. Beide instrumenten hebben immers ook één ader aan de massa. Als u hetzelfde doet bij een brugversterker gaat het mis. U sluit dan immers een van beide luidspreker aansluitingen kort naar de massa met de probe van uw oscilloscoop.

Het maximale vermogen in een normale versterker
Luidsprekers hebben impedanties van 4, 8 of 16 Ω. Het maximale vermogen dat u in zo'n luidspreker kunt opwekken hangt af van de maximale effectieve signaalspanning die de versterker naar de luidspreker kan sturen. Die maximale effectieve signaalspanning hangt weer af van de beschikbare voedingsspanning. Stel dat u, zoals getekend in de onderstaande figuur, een luidspreker hebt met een impedantie van 4 Ω. De eindversterker heeft voedingsspanningen van ±20 V. Om goed te werken moet er over de eindtransistoren een spanning van ongeveer 4 V blijven staan. Dat betekent dat de amplitude Uamp van de wisselspanning over de luidspreker maximaal 16 V bedraagt. Die waarde moet worden omgerekend in effectieve spanning:
Ueff = Uamp / 1,41
Ueff = 16 / 1,41
Ueff = 11,35 V
Het vermogen dat in een weerstand wordt gegenereerd wordt gegeven door de formule:
P = [Ueff]² / R
P = [11,35]² / R
P = 32,2 W
Meer vermogen is niet mogelijk, wat voor schakeling u ook verzint!
 |
| Het luidspreker vermogen in een 'normale' versterker. (© 2022 Jos Verstraten) |
Het maximale vermogen in een versterker-brug
Nu gaan wij berekenen welk vermogen er in deze luidspreker kan worden gegenereerd bij een versterker-brug met identieke voedingsspanningen. Het schema is getekend in de onderstaande figuur. Duidelijk blijkt dat er nu tussen beide luidspreker aansluitingen een spanning staat die twee keer groter is dan in het vorige voorbeeld. Dat komt doordat de groene aansluiting van de luidspreker nu niet aan de massa hangt, maar ook signaal voert ten opzichte van die massa. Beide signalen zijn in tegenfase. Als de rode luidspreker aansluiting op +16 V staat, staat de groene op -16 V. Er staat dus maximaal 32 volt over de luidspreker. Dat komt overeen met een effectieve waarde van 22,69 V. U kunt nu het in de luidspreker gedissipeerde vermogen berekenen: 128,7 W!
Dat is dus inderdaad, zoals gesteld in de inleiding, vier keer meer dan bij de traditionele eindversterker.
 |
| Het luidspreker vermogen in een versterker-brug. (© 2022 Jos Verstraten) |
Een versterker-brug met twee stuks TDA2030
Dank zij de verschilversterkers aan de ingang van dit IC is dat niet zo moeilijk. U kunt immers de ene TDA2030 schakelen als niet-inverterende versterker en de tweede als inverterende versterker. Als beide met hetzelfde signaal worden gestuurd, zullen de uitgangen twee 180° in fase verschoven signalen genereren, die u kunt gebruiken om de luidspreker in brug aan te sturen. Het schema is getekend in de onderstaande figuur. Het ingangssignaal gaat naar IC1 die als niet-inverterende versterker is geschakeld. Via de weerstand R7 wordt een klein deel van het in fase signaal aangeboden aan de inverterende ingang van IC2. Beide versterkers hebben identieke terugkoppel-elementen:
- IC1: R3, C4, R4
- IC2: R5, C5, R6
en versterken dus even veel. Op de twee uitgangen verschijnen signalen die in tegenfase zijn.
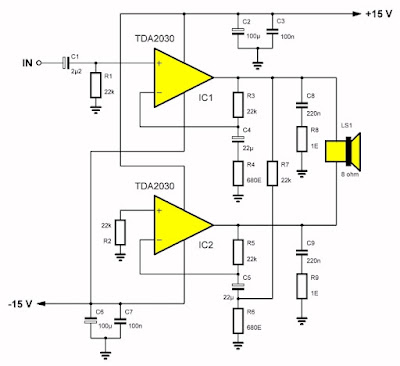 |
| Een versterker-brug met 2 x TDA2030. (© 2022 Jos Verstraten) |
Een versterker-brug met een TDA7266
Uiteraard zijn er ook complete brugschakelingen in één IC ontwikkeld. Een mooi voorbeeld is de TDA7266. Dit IC bevat twee versterker-bruggen met een maximaal vermogen van 2 x 7 W in 8 Ω luidsprekers bij een vervorming van 10 %. Het maximale vermogen daalt tot ongeveer 2 x 2 W als u de toelaatbare vervorming bij 1 % legt. U kunt het IC voeden uit een spanning tussen 3 V en 18 V. In de onderstaande figuur is het meest eenvoudige schema rond de TDA7266 voorgesteld, samen met de behuizing en de aansluitgegevens.
 |
Een versterker-brug met 1 x TDA7266. (© 2022 Jos Verstraten) |
De TDA7266 is courant leverbaar, onder andere bij Reichelt voor € 3,30. Interessant is dat bij diverse aanbieders op AliExpress een compleet bouwpakketje te koop is voor € 2,10. Zoals uit de onderstaande foto blijkt is de meegeleverde koelplaat wel veel te klein, maar dat is voor een ervaren doe-het-zelver uiteraard gemakkelijk te verhelpen.
 |
Een goedkoop bouwpakketje rond de TDA7266. (© AliExpress) |
Wheatstone-brug
Functie van de Wheatstone-brug
Met deze brug kunt u de waarde van een onbekende weerstand meten door deze in één zijde van de brug op te nemen, twee bekende weerstanden in twee overige zijden en een weerstandsdecade in de vierde zijde. Door deze decade af te regelen tot de brug in evenwicht is kunt u de waarde van de onbekende weerstand met een simpele formule berekenen.
Uitvinding van de Wheatstone-brug
Deze methode voor het meten van weerstanden werd voor het eerst bedacht in 1833 door Samuel Christie, maar werd in 1853 praktisch toegepast door Charles Wheatstone.
Samenstelling van de Wheatstone-brug
In de onderstaande figuur is de samenstelling van een Wheatstone-brug getekend. De weerstanden R1 en R3 zijn nauwkeurig bekende weerstanden, bijvoorbeeld exemplaren met een tolerantie van ±0,1 %. De weerstand R2 is de instelbare en afleesbare weerstanden decade. De weerstand Rx is de onbekende, te meten weerstand.
De Wheatstone-brug moet u voeden met een constante gelijkspanning Ub. In de tweede diagonaal zet u een gevoelige galvanometer M1. Bij het sluiten van de schakelaar S1 zal de naald van de galvanometer in een van de hoeken van de schaal terecht komen. U verdraait de knoppen van de weerstanden decadenbank tot de naald van de meter zo dicht mogelijk de nulstand in het midden van de schaal benadert.
 |
| De Wheatstone-brug. (© 2022 Jos Verstraten) |
Het berekenen van de onbekende weerstand
Als de naald van de galvanometer in het midden staat vloeit er geen stroom door het instrument. Dat kan alleen als de spanningen op de punten B en D aan elkaar gelijk zijn. Met de wet van Ohm kunt u beredeneren dat dit het geval is als:
R2 / R1 = Rx / R3
Uit deze vergelijking volgt:
Rx = [R2 / R1] • R3
De waarden van R1 en R3 zijn bekend, u kunt de waarde van R2 aflezen van de knoppen van de decadenbank.
Werken met de Wheatstone-brug
Met deze schakeling kunt u zeer nauwkeurig weerstanden meten, zeker als gebruik maakt van een zeer gevoelige galvanometer met bijvoorbeeld een bereik van -100 μA tot +100 μA. Om het leven van deze galvanometer te sparen moet u uiteraard wel een beetje met beleid te werk gaan. Betrek de Ub van een instelbare voeding en start de meting met een spanning van 0 V. De naald van de galvanometer staat dan uiteraard in de middenstand. Voer nu voorzichtig de spanning Ub een beetje op. U ziet dat de naald van de meter naar links of naar rechts uitslaat. Voer de spanning op tot de naald bijna in de hoek staat. Ga na spelen met de knoppen van de decadenbank tot de naald weer ongeveer in het midden staat. Voer dan de voedingsspanning verder op tot de naald weer vrijwel in een hoek staat. Regel dan de waarde van de decadenbank bij tot de naald weer ongeveer in het midden staat. Op deze manier kunt u de gevoeligheid van de meting tot ongekende hoogte opvoeren.
Het enige waar u op moet letten is dat de voedingsspanning niet zo hoog wordt dat de twee stromen de weerstanden gaan opwarmen. Dan kan de nauwkeurigheid immers in gevaar komen door de temperatuurscoëfficiënten van de onderdelen.
Wheatstone-bruggen en sensormetingen
De Wheatstone-brug is een ideale schakeling voor het 'normaliseren' van het uitgangssignaal van een sensor. Een voorbeeld zal dit verduidelijken. Stel dat u de temperatuur in een oven wilt meten met een PT100 sensor. Deze heeft een vrijwel lineaire weerstandsvariatie over een zeer groot temperatuurbereik. Het enige nadeel is dat de weerstand van zo'n sensor bij 0 °C 100 Ω is. U wilt echter dat er bij 0 °C ook 0 V wordt gemeten. Hoe die weerstand van 100 Ω om te zetten in een spanning van 0 V?
 |
De karakteristiek van een PT100 sensor. (© 2022 Jos Verstraten) |
Dat kan met een Wheatstone-brug, afgesloten met een verschilversterker, zie de onderstaande figuur. De brug wordt gevormd door de weerstanden R1 tot en met R5. Met de potentiometer R5 kunt u de brug zó afregelen dat er bij een temperatuur van exact 0 °C ook exact 0 V tussen de punten A en B staat. Wordt het kouder, dan wordt de spanning op punt A lager dan deze op punt B. Wordt het heter, dan wordt de spanning op dit punt hoger dan die op punt B. Beide punten gaan naar de ingangen van een verschilversterker, opgebouwd rond opamp1. Deze schakeling versterkt het spanningsverschil tussen de punten A en B met een factor die u kunt instellen met de instelpotentiometer R8.
 |
| Met een Wheatstone-brug kunt u de uitgangsspanning van een sensor ´normaliseren´. (© 2022 Jos Verstraten) |
Kelvin-brug, ook Thomson-brug genoemd
Vanwaar de naamsverwarring?
Thomson en Kelvin zij twee namen voor dezelfde persoon. William Thomson, die leefde van 1824 tot 1907, was een Britse natuurkundige. Vanwege zijn grote verdiensten voor de wetenschap werd hij in 1866 geridderd tot Sir William Thomson en in 1892 benoemd tot eerste Baron van Kelvin (een rivier ergens in een graafschap). In hetzelfde jaar werd hij, als eerste Britse wetenschapper, verheven tot lid van het House of Lords en werd dus Lord Kelvin.
Functie van de Kelvin-brug
Met de Kelvin-brug kunt u nauwkeurig weerstanden meten die een waarde hebben die lager is dan 1 Ω. Bij dergelijke kleine weerstanden gaat de weerstand van de aansluitdraden een niet te veronachtzamen rol spelen. De invloed van deze parasitaire weerstanden moet dus worden uitgesloten en dat is wat de Kelvin-brug doet.
Samenstelling van de Kelvin-brug
In de onderstaande figuur ziet u het principiële schema van een dergelijke brug. Weerstand Rx is weer de onbekende, te meten weerstand. Deze wordt in serie met een weerstand Rs op een spanningsbron aangesloten. Deze weerstand ligt in dezelfde grootteorde als de onbekende weerstand. De punten P1, P2, P3 en P4 zitten zo dicht mogelijk bij de aansluitingen van Rs en Rx.
 |
Het standaard schema van een Kelvin-brug. |
De werking van de Kelvin-brug
De weerstanden Rs, R1, R2 en Rx vormen een standaard Wheatstone-brug. Omdat de punten P1 en P4 dicht bij de componenten zitten hebt u geen last van de parasitaire weerstanden tussen de voedingsbron en de twee weerstanden Rs en Rx. Hetzelfde kan echter niet worden beweerd van de parasitaire weerstanden tussen Rs en Rx. Om deze te compenseren worden twee nieuwe takken ingevoerd met de weerstanden R3 en R4.
Het gaat te ver om in dit al zeer uitgebreid artikel de werking van de Kelvin-brug wiskundig volledig uit te werken. In de praktijk zorgt men ervoor dat de verhouding tussen de weerstanden R1 en R2 gelijk is aan de verhouding tussen de weerstanden R3 en R4. De brug wordt zo goed mogelijk in balans gebracht, bijvoorbeeld door de weerstand Rs uit te voeren onder de vorm van geijkte weerstanden die een na een in de brug worden gezet tot de galvanometer een zo goed mogelijk evenwicht aangeeft. Bij balans kunt u de onbekende weerstand berekenen met de formule:
Rx = R2 • [Rs / R1]
Om de nauwkeurigheid zo groot mogelijk te maken is het van belang dat er over Rs en Rx zo groot mogelijke spanningen vallen. Men meet meestal met de maximale stroom die door deze weerstanden mag vloeien.
De Kelvin-brug in de praktijk
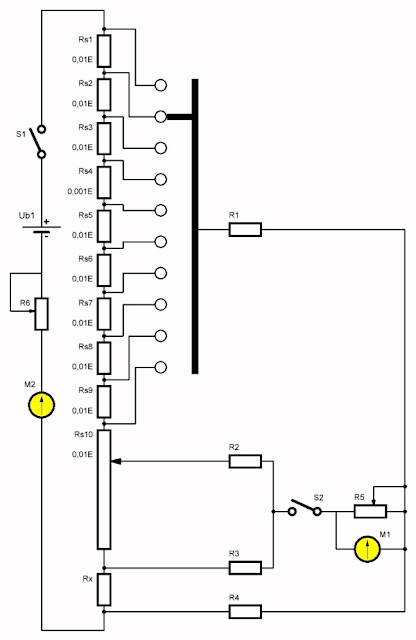 |
| Schema van een Kelvin-brug voor het meten van heel kleine weerstanden. (© 2022 Jos Verstraten) |
De QJ57 van Tinsley
Een apparaat dat werkt volgens het principe van de Kelvin-brug is de QJ57 van Tinsley. Met dit apparaat kunt u weerstanden in het mΩ bereik meten. De prijs van een dergelijk apparaat bedraagt ongeveer € 750,00.
 |
| De Kelvin-brug QJ57 van Tinsley. (© AliExpress) |
Maxwell-brug
Functie van de Maxwell-brug
Met deze schakeling kunt u spoelen of zelfinducties meten. Het is een variatie op de Wheatstone-brug, waarbij een van de weerstanden is vervangen door een condensator en de brug niet met gelijkspanning, maar met wisselspanning wordt gevoed. De brug wordt soms ook Maxwell-Wien genoemd.
Uitvinding van de Maxwell-brug
Deze schakeling werd bedacht door de wereldberoemde James C. Maxwell, die zijn brug voor het eerst beschreef in 1873.
Samenstelling van de Maxwell-brug
De brug is volgens het onderstaande schema samengesteld. U herkent ongetwijfeld de structuur van de Wheatstone-brug, waarbij twee takken vervangen zijn door de te meten spoel en een bekende condensator. De weerstand Rx is de inwendige weerstand van de spoel Lx.
Een ander fundamenteel verschil is dat u nu geen DC-voeding kunt gebruiken voor het voeden van de schakeling, maar dat u een beroep moet doen op een wisselspanning. De frequentie van dit signaal speelt geen rol, zodat u bijvoorbeeld de secundaire spanning van een voedingstrafo kunt gebruiken. De consequentie hiervan is dat een standaard galvanometer niet meer bruikbaar is, maar dat u een wisselspannings- of stroommeter in de brug moet opnemen. De reeds vermelde gevoelige hoofdtelefoon kan natuurlijk ook.
 |
| Het principe van de Maxwell-brug. (© 2022 Jos Verstraten) |
Het berekenen van de onbekende spoel Lx
De weerstanden R1 en R4 zijn bekende nauwkeurige weerstanden. Voor R2 en voor C1 worden geijkte decadenbanken gebruikt. Het meetprincipe gaat uit van het feit dat zowel een condensator als een spoel een faseverschuiving veroorzaken tussen de spanning over het onderdeel en de stroom die door het onderdeel vloeit. Die faseverschuivingen zijn echter wél tegengsteld! Bij een spoel zal de stroom na-ijlen op de spanning, bij een condensator ijlt de stroom voor op de spanning.
Het is de bedoeling dat u de brug in evenwicht brengt op zowel amplitude- als op fase-gebied. Het ene doet u met de weerstand R2, het tweede met de condensator C1. Als de brug in evenwicht is kunt u de waarde van de condensator C1 en R2 aflezen. De waarde van de spoel wordt dan gegeven door de formule:
Lx = R1 • R4 • C2
en de waarde van de inwendige weerstand van de spoel door:
Rx = [R1 • R4] / R2
Wien-brug
Functie van de Wien-brug
De Wien-brug is ontworpen voor het nauwkeurig meten van de waarde van de frequentie van een sinusvormig signaal in het audio-gebied. Dit signaal is ook de voedingsspanning van de brug.
Uitvinding van de Wien-brug
Deze brug werd ontwikkeld door de Duitse natuurkundige Max Wien in 1891 als hulpmiddel bij zijn onderzoek naar de sterkte en de voortplanting van geluiden van diverse frequenties.
De samenstelling van de Wien-brug
De Wien-brug bevat vier weerstanden en twee condensatoren. Twee instelbare weerstanden moeten aan elkaar gelijk zijn. Hetzelfde geldt voor de twee condensatoren.
 |
| Het principe van de Wien-brug. (© 2022 Jos Verstraten) |
Het berekenen van de onbekende frequentie
Voorwaarde voor het goed werken van deze brug is dat beide condensatoren exact aan elkaar gelijk zijn. In de praktijk schakelt men met bijvoorbeeld met een 2 x 4 standen draaischakelaar twee identieke condensatoren in een 1/10/100/1.000 verhouding in de kring. Ook de twee weerstanden R1 en R3 moeten identiek zijn. Dat kan door voor deze weerstanden een stereo-potentiometer te gebruiken en deze op de frontplaat van het apparaat te voorzien van een geijkte schaal. Ook deze brug moet een meetinstrument hebben dat in staat is wisselspanning te meten in het frequentiebereik waarvoor de brug wordt ontworpen.
De brug wordt in evenwicht gebracht door eerst met de draaischakelaar de condensatoren te selecteren en nadien af te regelen om minimale uitgangsspanning met de stereo potentiometer. Als de brug op deze manier in evenwicht is gebracht kunt u de frequentie van het ingangssignaal berekenen met de formule:
f = 1 / [2 • π • R • C]
waarin:
π = het beroemde getal pi, dus 3,141592653...
R = R1 = R3
C = C1 = C2
De Wien-brug in oscillatorschakelingen
Het zal duidelijk zijn dat de Wien-brug volstrekt verouderd is voor het meten van frequenties. Kristal-gestuurde digitale frequentiemeters zijn veel gemakkelijker te bedienen en hebben een veel hogere nauwkeurigheid. Tóch wordt de Wien-brug nog heel vaak toegepast en wel in sinusgeneratoren. Zoals uit het schema van de onderstaande figuur volgt, is de Wien-brug samengesteld uit een parallel schakeling van een weerstand en een condensator (R2/C2) en een serie schakeling van identieke componenten (R1/C1). Als beide weerstanden en beide condensatoren even groot zijn, kunt u de oscillatiefrequentie berekenen uit de formule:
fo = 1 / [2 • π • R • C]
Deze schakeling vereist het gebruik van twee versterkertrappen omdat de 180° fasedraaiing, die door de eerste trap wordt geïntroduceerd, door de tweede trap moet worden opgeheven. In- en uitgang van de versterker moeten dus in fase zijn! Om aan de algemene amplitude voorwaarde van een oscillator te voldoen moet de totale versterking groter dan drie zijn. Dit is een gevolg van de spanningsdeling die door het netwerk van de brug van Wien tussen de uitgang en de ingang ontstaat en het teruggekoppelde signaal verzwakt.
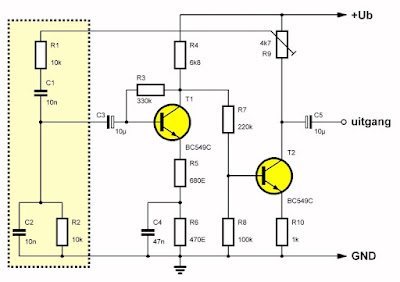 |
| De Wien-brug toegepast in een sinusoscillator (© 2022 Jos Verstraten) |
Met de weerstand R9 kunt u de koppelfactor instellen en de schakeling aan de amplitude voorwaarde (versterking groter dan 3) laten voldoen. Om de waarde van de versterkingsfactor op precies deze drie te stabiliseren moet de schakeling worden voorzien van een aantal terugkoppelingen. Bij de getoonde schakeling (een van de vele) wordt er zowel aan spanning- als aan stroomtegenkoppeling gedaan. De weerstand R3 stabiliseert de eerste versterkertrap, de weerstanden R5 en R10 zorgen voor een stroomtegenkoppeling in de emitterleidingen van de twee halfgeleiders.

U kunt de frequentie van de schakeling variëren door ofwel de twee weerstanden ofwel de twee condensatoren van de brug in gelijke mate te veranderen. In de praktijk zal men meestal met behulp van een dubbele omschakelaar een aantal identieke condensatoren in het netwerk opnemen. Als u deze een 1 op 10 verhouding geeft kunt u dan de frequentie van de schakeling met deze schakelaar decadisch instellen. De twee vaste weerstanden worden vervangen door een stereo-potentiometer, waarmee u de frequentie in iedere decade op iedere gewenste waarde kunt instellen.
Over de Wien-brug oscillator is op dit blog een eigen artikel geschreven met bruikbare voorbeeldschakelingen:
Aanklikbare link ➡ Schakelingen: sinusgeneratoren
De Sauty-brug
Meten van condensatoren
Deze brug is rechtstreeks gebaseerd op de Wheatstone-brug en is bedoeld voor het meten van de waarde van een condensator. De brug wordt (uiteraard) gevoed met een wisselspanning en u moet dus ook een AC-meter in de andere diagonaal zetten. De waarde van de onbekende condensator volgt uit de formule:
Cx = C1 • [R2 / R1]
 |
De brug van De Sauty. (© 2022 Jos Verstraten) |
Schering-brug
Meten van de capaciteit en de ESR van condensatoren
Met deze brug, voorgesteld in de onderstaande figuur, kunt u niet alleen de capaciteit van een condensator bepalen, maar ook zijn ESR of equivalente serie weerstand. In het schema zijn deze twee grootheden voorgesteld door Cx en Rx. De brug wordt in evenwicht gebracht door het afregelen van R1 en C1. Bij evenwicht kunt u de waarde van de twee te meten grootheden berekenen met de onderstaande formules:
Cx = [R1 • C3] / R2
en
Rx = [C1 • R2] / C3
 |
| De brug van Schering. (© 2022 Jos Verstraten) |
De Schering-brug in de praktijk
Dergelijke apparaten treft u niet aan in de meeste elektronica werkplaatsen. Tóch zijn er fabrikanten die dergelijke exotische producten maken, zoals het onderstaande model van ASICO bewijst.
 |
| Een laboratorium-uitvoering van de brug van Schering. (© IndiaMART) |
Murray-brug
Het bepalen van aardlekken in kabels
Met deze brug kunt u de plaats lokaliseren waar een ondergrondse kabel een sluiting naar de aarde vertoont, een zogenaamde aardlek. Het basisschema is voorgesteld in de onderstaande figuur. Een twee-aderige kabel met een totale lengte van L heeft een goede geleider en een geleider die een lek naar de aarde vertoont. De kabel is voorgesteld door de weerstanden Rg, Rx en Ry. Rg is de aderweerstand van de totale lengte L van de kabel, Rx en Ry zijn de aderweerstanden tot vóór en van ná de aardlek. Rf is de lekweerstand naar aarde van de defecte ader. De twee aders van de kabel worden aan het ene einde van de kabel met elkaar verbonden. U sluit dus de kabel kort. Beide aders van de kabel worden aan het ander einde met de weerstanden R1 en R2 verbonden met een gelijkspanningsbron die een forse spanning levert. De andere pool van deze voeding ligt aan de aarde. U hebt dus duidelijk een brug gemaakt met de vier weerstanden en de spanningsbron. Uiteraard zet u een galvanometer in de andere diagonaal.
De brug wordt in evenwicht gebracht door het variëren van de weerstanden R1 en R2. Als de brug in evenwicht is kunt u de lengte Lx berekenen met de formule:
Lx = 2 • L • [R1 / (R1 + R2)]
 |
| Met de Murray-brug kunt u de plaats van een aardlek in een kabel bepalen. (© 2022 Jos Verstraten) |
Carey-Foster-brug
Meten van zeer lage weerstandswaarden
De Carey-Foster-brug werd in 1872 beschreven door Carey Foster. Het is een variatie op de traditionele brug van Wheatstone voor het meten van zeer lage weerstandswaarden. De basisopzet is getekend in de onderstaande figuur. Rx is de weerstand die moet worden gemeten. R1, R2 en Ry zijn drie weerstanden in ongeveer dezelfde grootteorde als Rx, maar waarvan de waarden zeer nauwkeurig bekend zijn. Links en rechts ziet u twee grote metalen contactoppervlakken, waarvan de weerstand zo goed als nul is. Tussen deze oppervlakken is een lange laagohmige weerstandsdraad A~B aangebracht met een bekende lengte L. Op deze draad kunt u een klem C schroeven. Het geheel wordt gevoed door een gelijkspanningsbron Ub die een lage spanning levert, maar in staat is een zeer grote stroom te leveren. De zwarte cirkels stellen de punten voor waar de diverse onderdelen zo laagohmig mogelijk met elkaar worden verbonden.
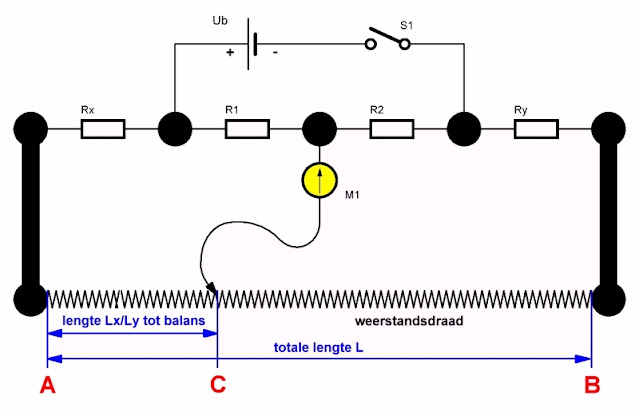 |
| De principiële opzet van een Carey-Foster-brug. (© 2022 Jos Verstraten) |
De meting start door het verplaatsen van het contact C over de weerstandsdraad tot de Carey-Foster-brug in balans is. De naald van de galvanometer M1 staat in het midden van de schaal. U leest nu de lengte Lx af en berekent deze procentueel ten opzichte van de totale lengte L. Noem deze verhouding %x. Wissel dan Rx en Ry van positie en bepaal een nieuw balanspunt van contact C. Lees nu de lengte Ly af en zet deze lengte weer op in een procentueel getal ten opzichte van de totale lengte van de weerstandsdraad. Noem deze verhouding %y. Bereken de weerstand van de draad per procent en noem deze %totaal. De weerstand van Rx volgt dan uit de formule:
Rx = [&totaal • (%y - %x)] + Ry
Tot slot van dit lange verhaal....
De minst toegepaste bruggen
Er zijn in de loop van de geschiedenis nog meer brugschakelingen ontworpen. Deze hebben echter de tand des tijds niet overleeft en u zult deze niet meer tegenkomen. Wij vermelden deze schakelingen hier tóch zonder toelichting of schema's om dit verhaal compleet te maken.
Anderson-brug
Dit is een schakeling die in 1891 door Alexander Anderson werd afgeleid van de Maxwell-brug en die werd ontworpen voor het meten van de waarde en de serieweerstand van een spoel. De formules voor het berekenen van de twee grootheden uit het brugevenwicht zijn echter complex en de brug is zeer gebruikersonvriendelijk vanwege de nogal omslachtige afregeling.
Hay-brug
Is ook een van de Maxwell-brug afgeleide schakeling die werd ontworpen voor het meten van zeer hoge zelfinducties. Ook deze brug genereert vrij complexe formules voor het berekenen van de waarde van de zelfinductie.
Fontana-brug
Een vrij ingewikkelde schakeling die in 2003 werd beschreven door Giorgio Fontana en waarmee een spanning-naar-stroom omzetter kan worden ontworpen. Het unieke is dat deze schakeling ook werkt voor wisselspanning en een grote bandbreedte heeft.
Lattice-brug
Deze schakeling is een fase-equaliser die in 1927 werd uitgevonden door Otto Zobel. De verzwakking en impedantie van het filter zijn frequentie-onafhankelijk, maar hetzelfde geldt niet voor het faseverschil tussen de ingang en de uitgang. Dit neemt toe naarmate de frequentie van het signaal stijgt. Dergelijke bruggen werden toegepast om fase-verschuivingen tussen het linker en rechter kanaal van een stereosignaal te compenseren.
